Безвихревое движение жидкости

Дата: 2025-06-14; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Во многих случаях при исследовании движения жидкости можно не учитывать вращения из-за пренебрежимо малых угловых скоростей ча­стиц. Такое движение называется безвихревым.

Для безвихревого потока 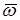=0 (или rotV=0) и, следовательно, равны нулю компоненты вихря w x , w y , w z. В соответствии с этим [4] можно записать

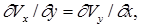
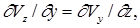
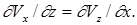(1.1)

Эти равенства являются необходимым и достаточным условием того, чтобы дифференциальный трехчлен ( Vxdx + Vydy + Vzdz ) был полным дифференциалом некоторой функции, характеризующей поток жидкости так же, как функции скоростей Vx , Vy , Vz .

Обозначив эту функцию в виде j (х, у, z , t ) и рассматривая время t в качестве параметра, можно записать следующее выражение:

.

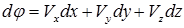С другой стороны, этот же дифференциал

.

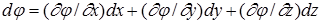Сравнивая два последних выражения, находим

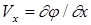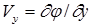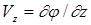, , . (1.2)

Функция j называется потенциалом скоростей или потен­циальной функцией, а безвихревой поток, характеризуемый этой функцией, - потенциальным. Из соотношений (1.2) следует, что частная производная от потенциала j по координате равна проекции скорости на соответствующую координатную ось. Это свойство потенци­альной функции сохраняется и для произвольного направления. В част­ности, тангенциальная составляющая скорости в какой-либо точке на произвольной кривой s будет равна частной производной: 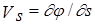, а нормальная составляющая 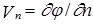, где п — нормаль к дуге s в рас­сматриваемой точке. Для полярных координат r и q проекции вектора скорости 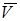некоторой точки на направление полярного радиуса-вектора и на направление, перпендикулярное этому радиусу-вектору, будут рав­ны соответственно частным производным:

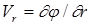и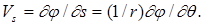

Как видно, величина скорости в каком-либо направлении опреде­ляется быстротой изменения потенциала j в том же направлении. Если рассматривается направление s , то быстрота изменения потенциала рав­на частной производной по этому направлению: 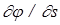. Величину 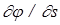можно рассматривать как проекцию на направление s некоторого век­тора, называемого градиентом функции j и совпадающего с направлением наиболее быстрого возрастания этой функции. Очевидно, этот вектор равен вектору скорости 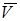. Обозначая градиент функции в виде grad j, можем написать

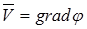(1.3)

или

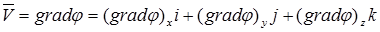, (1.4)

где коэффициенты в скобках в правой части представляют собой проекции вектора градиента скорости на оси координат:

, ,

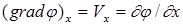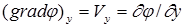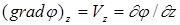. (1.5)

Использование потенциальной функции существенно упрощает иссле­дования движения жидкости, так как вместо определения трех неизвестных, какими являются составляющие скорости Vx , Vy , Vz , достаточно найти одну неизвестную функцию j и тем самым полностью рассчитать поле скоростей.

Функция тока

Изучение безвихревого течения газа упрощается, если свести его к отысканию одной неизвестной потенциальной функции, полностью определяющей это течение. Покажем, что для некоторых видов вихревого потока существует функция, также определяющая его кинематические характеристики.

Рассмотрим двухмерное (плоское или пространственное осесимметричное) установившееся вихревое движение жидкости. Из уравнения неразрывности [5]

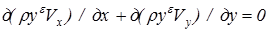, (1.6)

где для двухмерного плоского течения e = 0, а для двухмерного осесимметричного потока e =1, y = r, можно установить, что существует некоторая функция y координат х, у, определяемая соотношениями:

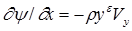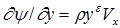; . (1.7)

Действительно, подставляя эти соотношения в (1.6), получаем 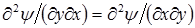, т. е. тождество. Внося (1.6) в уравнение линий тока V у dy = Vxdx , представленное в виде

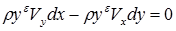, (1.8)

получаем выражение

,

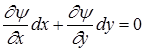из которого следует, что (1.8) представляет собой дифференциал функции y и, следовательно,

d y =0. (1.9)

Интегрируя (1.9), найдем уравнение линий тока в виде

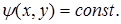(1.10)

Функция y, называемая функцией тока, полностью определяет скорости вихревого потока в соответствии с соотношениями

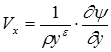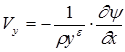, . (1.11)

Семейство линий тока потенциального потока можно также ха­рактеризовать функцией y = const , которая связана с потенциалом скоростей соотношениями

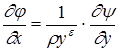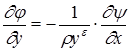, . (1.12)

Полагая в (1.11) и (1.12) r = const, получаем соответствующие выражения для несжимаемого потока:

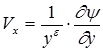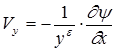, ; (1.13)

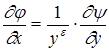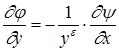, . (1.14)

Принимая в последних равенствах e =0, получаем для несжимаемого плоского потока уравнения

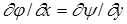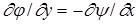, . (1.15)

Зная потенциал скоростей, исходя из этих уравнений, можно опреде­лить с точностью до произвольной постоянной функцию тока и наоборот.

В потенциальном потоке наряду с линиями тока можно провести семейство эквипотенциальных кривых (на плоскости) или эквипотен­циальных поверхностей (в осесимметричном потоке), определяемое уравнением j = const . Рассмотрим векторы

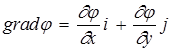и ,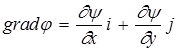

направления которых совпадают с направлениями нормалей соот­ветственно к кривым j =const и y = const . Скалярное произведение этих векторов

.

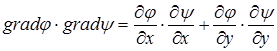Учитывая формулы (1.2) и (1.11), можно установить, что это скалярное произведение равно нулю. Из этого следует, что линии тока будут ортогональны к эквипотенциальным линиям (на плоскости) или эквипотенциальным поверхностям (в осесимметричном потоке).