Достоверное: учебный год когда-нибудь закончится, все люди смертны, мама старше своих детей, …
Случайное: бутерброд упадет маслом вниз, завтра будет дождь, завтра будет видно Меркурий,…
Историческая справка.
Вопрос о возможности измерения степени достоверности наступления какого-либо события задавали себе многие ученые. Основателями теории вероятности были французские математики XVII века Б. Паскаль и П. Ферма, а также голландский ученый Х. Гюйгенс.
Зарождение теории вероятностей началось с того, что придворный французского короля, шевалье (кавалер) де Мере (1607-1648), сам азартный игрок, обратился к французскому физику, математику и философу Блезу Паскалю (1623-1662) с вопросами к задаче об возможных очках при игре в кости. До нас дошли два знаменитых вопроса де Мере к Паскалю: 1) сколько раз надо бросить две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний; 2) как справедливо разделить поставленные на кон деньги, если игроки прекратили игру преждевременно? Паскаль обратился к математику Пьеру Ферма (1601-1665) и переписывался с ним по поводу этих задач. Они вдвоем установили некоторые исходные положения теории вероятностей.

| 
| 
|
| Пьер Ферма | Блез Паскаль | Христиан Гюйгенс |
Долю успеха того или иного события математики называют вероятностью этого события (от латинского probabilitas – «вероятность»)
Исходы в определённом опыте называются равновозможными, если шансы этих исходов одинаковы. Например, монета с одинаковой вероятностью упадет одной из своих сторон вверх, на игральной кости выпадет 1 или 6 очков.
Исходы, при которых происходят некоторое событие, называют благоприятными исходами данного события.
Рассмотрим, например, событие В «выпадение четного числа очков при одном бросании игральной кости». Это событие наступает в трех случаях – когда выпадет 2, или 4, или 6 очков. Все эти исходы благоприятные событию В. Равновозможных исходов 6, тогда Р(В) = 3/6 = 1/2. Вероятностью равновозможного события в некотором испытании равно отношение числа благоприятных для него исходов (n) к числу всех равновозможных событий (m)
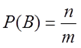
- Физкультминутка.
Поднимает руки класс – это раз.
Повернулась голова – это два.
Руки вниз, вперед смотри – это три.
Руки в стороны пошире, развернули на четыре,
С силой их к плечам прижать – это пять.
Всем ребятам надо сесть – это шесть.
- Формирование умений решать задачи (различать благоприятные и всевозможные события, применят формулу).
1)Выполнение заданий учебника № 798, 800, 801 с обсуждением хода решения у доски.
- Разбор «классических» случаев количества всевозможных событий при бросании симметричной монет и игровой кости (кубика).
| 1 монета | 2 монеты | 3 монеты | 1 кубик | 2 кубика | 3 кубика |
| О Р | 00 РР ОР РО | ООО ОРО РОО ООР РРО РОР ОРР РРР |
| 11 21 31 41 51 61 12 … 62 13 … 14 … 15 65 16 … 66 | 111 112 113 … |
| 2 | 2 2 =4 | 2 3 =8 | 6 | 6 2 =36 | 6 3 =216 |
Данную таблицу записать в тетради
- Самостоятельная работа.
| Вариант 1 1.Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что начинать игру должна будет девочка. 2. На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 17 с капустой и 9 с вишней. Стас наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. 3. В среднем из 200 карманных фонариков, поступивших в продажу, восемь неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен. 4. В фирме такси в данный момент свободно 20 машин: 4 чёрных, 6 жёлтых и 10 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси. 5. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно 1 раз. | Вариант 1 1.На экзамене 20 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет. 2. На каждые 1000 электрических лампочек приходится пять бракованных. Какова вероятность купить исправную лампочку? 3.В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл выпадет ровно 2 раза. 4. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России. 5. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4. |
- Подведение итогов урока. Рефлексия.
- Комментирование и запись домашнего задания. П.35 №799, 802,806, дополнительно индивидуально задания для подготовки к экзаменам.








