Преобразование суммы и разности тригонометрических функций в произведение.
Урок 2 ( тесты).
Преобразование суммы и разности тригонометрических функций в произведение.
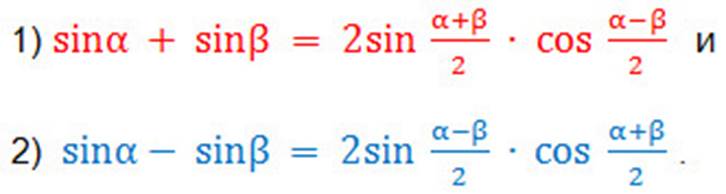
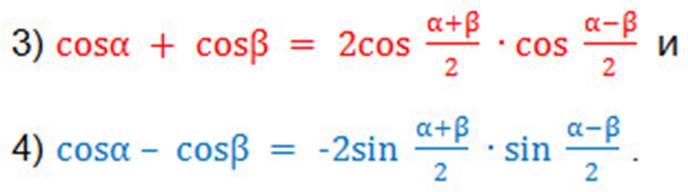
1. Упростить: sin20°+sin40°.
A) sin10°; B) cos10°; C) cos20°; D) sin20°; E) tg10°.
2. Преобразовать в произведение: cos47°+cos73°.
A) cos46°; B) sin46°; C) sin13°; D) cos120°; E) cos13°.
3. Вычислить: cos75° + cos15°.
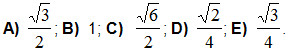
4. Разложить на множители: sin40°+sin50°.
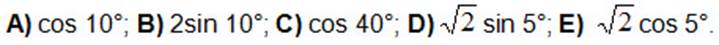
5. Представить в виде произведения: sin 15° + cos 65°.
A) sin 40°cos 25°; B) sin 25°cos 40°; C) 2sin 25 cos 40°;
D) sin 80°; E) 2sin 20°cos 5°.
6. Представить в виде произведения: cos 40° – sin 16°.
A) 2sin 17°cos 33; B) 2cos 17°sin 33°; C) 2sin 17°sin 33°;
D) 2cos 17°cos 33°; E) 2sin 56°.
7. Вычислить: cos 85°+ cos 35° – cos 25°.
A) 0; B) 1; C) cos 40°; D) sin 40°; E) -1.
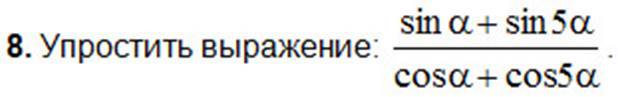
A) ctg3α; B) tg3α; C) tg6α; D) ctg6α; E) 1.
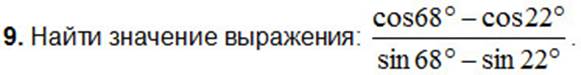
A) 1; B) 0; C) cos 80°; D) -1; E) sin 80°.
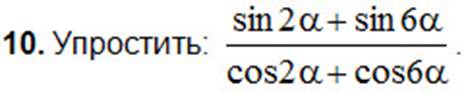
A) tg2α; B) tg4α; C) ctg4α; D) ctg2α; E) cos4α.
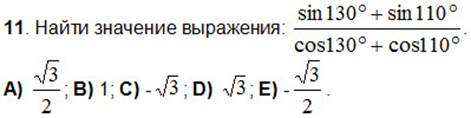
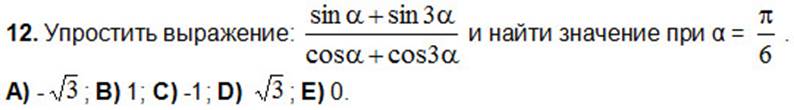
Преобразование произведения тригонометрических функций в сумму.
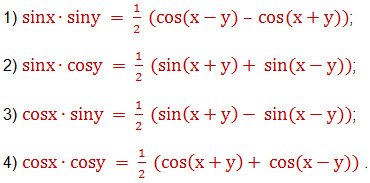
1. Упростить: sin75°sin15°.
А) 0,25; В) 0,5; С) 1; D) -0,5.
2. Упростить: cos40°cos20°.
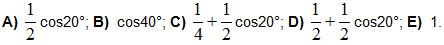
3. Преобразовать в сумму: sin(30°+x)cos(30°- x).
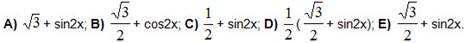
4. Вычислить произведение: sin15°cos75°.
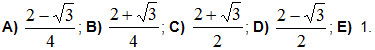
5. Вычислить: sin 45°cos 15°.
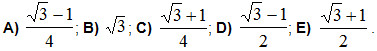
6. Записать в виде суммы произведение синусов:
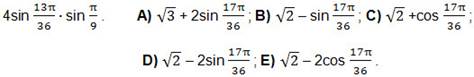
7. Представить в виде суммы произведение косинусов:
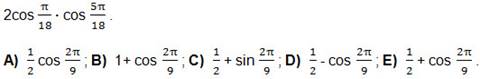
8. Запишите в виде суммы произведение:
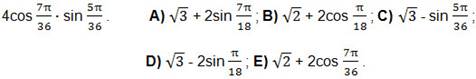
9. Вычислить: sin 15°cos 7° – cos 11°cos 79°.
A) sin 8°; B) 0,5sin 8°; C) cos 22°; D) 0,5cos 22°; E) sin 11°.
10. Упростить выражение: 2cos 20°cos 40° – cos 20°.
А) -0,5; B) 0; C) 1; D) -1; E) 0,5.
11. Вычислить: sin 10°sin 50°sin 70°.
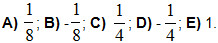
12.Упростить: 8cos 10°cos 20°cos 40° .
A) ctg10°; B) tg10°; C) –tg10°; D) –ctg10°; E) tg20°.








