Тема 4. Случайная изменчивость.
7 класс Теория вероятностей и статистика
ТЕМА 4. СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ.
ЧАСТОТА ЗНАЧЕНИЙ В МАССИВЕ ДАННЫХ.
1. Запишите в тетради:
Девятое января(7А)
Шестнадцатое января(7В)
Девятнадцатое января(7Б)
Дистанционная работа
Случайная изменчивость. Относительная частота случайных событий.
О некоторых событиях мы можем твердо сказать, что они произойдут. В наступлении других событий мы не так уверены. Например, в самый жаркий и солнечный летний день мы твердо знаем, что лето кончится, наступит осень, а затем зима. Но невозможно сказать заранее, будет эта зима теплой или холодной.
Мы также не можем предвидеть, будет ли следующий год влажным или засушливым, урожайным или нет, хотя все эти события влияют на нашу жизнь. В неурожайный год дорожает хлеб, предприятия сельского хозяйства несут убытки, а некоторые из них могут разориться. Урожайный год тоже лучше бы предвидеть (хотя бы затем, чтобы приготовить хранилища для зерна).
Нельзя предвидеть многие события даже недалекого будущего. Например, летом при некоторых состояниях атмосферы грозы становятся частыми. Но и ´ тогда нельзя предвидеть утром, будет ли гроза днем. Можно лишь говорить о шансах этого события. В прогнозах погоды эти шансы стараются учесть. Там можно встретить выражения вроде «дождь сегодня маловероятен», «вероятность дождя 10 %», «к вечеру возможно усиление ветра» и т. п.
Для нефтедобывающих стран, к которым относится Россия, важны международные цены на нефть. Безошибочно предвидеть эти цены не удается, хотя многие стараются это сделать. При составлении бюджета государства на следующий год важно знать, превысит ли средняя цена на нефть некоторый уровень или нет. Если превысит, то в бюджете можно предусмотреть определенные траты, а если нет — то нельзя. Например, бюджет России на 2004 г. был составлен, исходя из предположения, что средняя цена окажется не меньше 22 долларов за баррель. (Баррель — от «бочка» — единица объема, принятая для нефти; примерно 159 литров.) Предполагается, что с большой вероятностью реальная цена окажется выше этой.
Перед началом футбольного чемпионата мы не можем с полной уверенностью назвать ни победителя, ни призеров. Мы можем обсуждать шансы различных команд, говорить об их вероятностях на победу, но лишь по окончании чемпионата станет ясно, кто и какое место в нем занял. Все упомянутые выше события — случайные
Определение. Мы называем событие случайным, если нельзя утверждать, что это событие в данных обстоятельствах непременно произойдет.
Примеры случайных событий можно приводить и описывать бесконечно. Невозможно предсказать длительность начавшегося или будущего телефонного разговора; нельзя знать, сколько ошибок сделает школьник в предстоящей контрольной работе. При бросании игральной кости невозможно предсказать, какая из шести граней выпадет. Невозможно предвидеть число крупных пожаров в городе на будущей неделе, число землетрясений в будущем году. Невозможно предвидеть, на какой билет лотереи выпадет главный выигрыш, и множество иных событий.
2. Ответить на вопросы (устно):
1). Какие события мы называем случайными?
2). Является ли случайным событие «Меня завтра спросят на уроке»?
3). Является ли случайным событие «Летом у меня будут каникулы»?
4). Является ли случайным событие «Мне сегодня встретится черная кошка»?
5). Приведите примеры случайных событий из вашей школьной жизни.
| В повседневной жизни, в практической и научной деятельности проводят наблюдения и эксперименты за различными случайными событиями, которые могут произойти или не произойти. Например, поражение мишени при выстреле, выигрыш спортивной команды и другие. |
| Закономерности случайных событий изучает раздел математики, который называется теорией вероятностей. Одним из вопросов, из которого зародилась теория вероятностей, был вопрос о том, как часто наступает то или иное событие. Французский ученый Блез Паскаль, один из создателей этой науки. Русский математик Андрей Колмогоров внес большой вклад в развитие теории вероятностей. |
| Рассмотрим классические примеры задач из теории вероятностей. Задача1. Бросание монеты. Отмечают упадет она сверху орлом или решкой. Задача 2. Бросание игральных кубиков. Наблюдали сколько раз выпадет цифра, например, 6. При небольшом числе испытаний закономерности могут не просматриваться. Однако, если испытания проводятся много раз, то выявляется определенная закономерность. |
| Пусть некоторое испытание проводится n раз, при этом определенное событие наступает m раз. Число m называют частотой события, а отношение m к n – относительной частотой события. Такой подход к определению вероятности называют статистическим. |
Приведем пример: бросали 100 раз игральный кубик. При бросании на верхней грани может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждое событие является случайным. Пусть цифра 6 выпала 17 раз. Частота события
m =17. Относительная частота этого события равна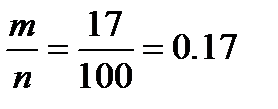 
|
Многие исследователи проводили испытания с бросанием монеты, например, английский ученый Карл Пирсон бросал монету 24000 раз. Вычисляли относительную частоту выпадения орла. Оказалось, что каждый раз относительная частота выпадения орла незначительно отличалась от  .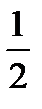
|
Подведем итог: при статистическом подходе в теории вероятностей проводится длинная серия опытов в одинаковых условиях со случайными исходами, в которых определяется частота события m и рассчитывается относительная частота события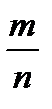 
(Обращаю ваше внимание, что относительная частота – это безразмерное дробное число, записанное точной десятичной или обыкновенной дробью.)
|
3. Просмотрите в Российской электронной школе Урок №45 «Относительная частота случайного события» (Алгебра. 9 класс) по ссылке: https://resh.edu.ru/subject/lesson/2571/start/
4. В этом же уроке из тренировочных упражнений выполнить: № 1(выписать правильные ответы), № 2 и № 5(решить задачи), №3 (записать относительные частоты в каждой серии испытаний), № 7 и № 8 (правильно подсчитайте буквы и найдите ответ)
5. Прочитайте п. 21 из учебника. Упражнения №1, №2, №3(стр.79) – устно.
Напоминаю, что в заданиях не достаточно записать только ответ без условия. Необходимо кратко записать условие, решение и ответ. В каждом номере домашнего задания в скобках указано, что необходимо сделать).
Выполненные работы выслать до следующего урока включительно в Дневник.ру или на эл.почту: barchan 7@ gmail . com
Не торопитесь, отвечайте на все вопросы и правильно оформляйте решение в тетрадях.
Консультации, справки, вопросы можно по телефону: 0714520659 – Людмила Николаевна.
Домашнее задание: Почувствуйте себя в роли исследователя - подбросьте любую монету 50 раз и подсчитайте, сколько раз выпадет орел. Результат округлите до сотых.