Методы приближенного решения уравнений. Метод касательных
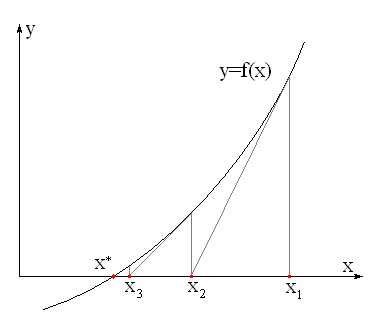
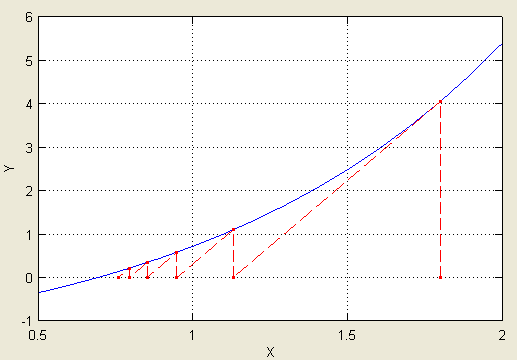
Классический метод Ньютона или касательных заключается в том, что если xn – некоторое приближение к корню x* уравнения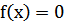 
, то следующее приближение определяется как координата пересечения касательной с осью ОХ, проведенной в точке xn.
Уравнение касательной к функции f(x) в точке xn имеет вид:
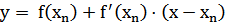
В уравнении касательной положим y=0 и x=xn+1.
Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:
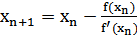(1)
Сходимость метода очень быстрая.
Здесь x0, x1, x2 … последовательные приближения к корню x*, полученные в результате применения метода Ньютона. Ясно, что сходимость последовательности {xk} к корню зависит от свойств функции f(x) и не всегда имеет место. Так, легко представить, что уже приближение x1 не попадает на исходный интервал и процесс итераций останавливается. Приведём полезную теорему, гарантирующую в некоторых случаях сходимость метода Ньютона.
Теорема
Если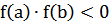 
, причём 
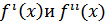отличны от нуля (и, следовательно, сохраняют определённые знаки при x ∈ [a, b]), то, исходя из начального приближения x0 ∈ [a, b], удовлетворяющего условию 
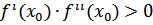, можно вычислить методом Ньютона по формуле (1) единственный корень x* уравнения (1) с любой степенью точности.
Замечание. Практическим критерием окончания вычислений является выполнение условия |xn+1 − xn| < ε, где ε – требуемая точность вычисления корня.
К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие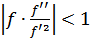 
, в противной ситуации сходимость есть лишь в некоторой окрестности корня.
Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.
Обоснование
Чтобы численно решить уравнение f(x)=0, его необходимо привести к эквивалентному уравнению: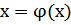 
, где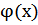 
— сжимающее отображение.
Для наилучшей сходимости метода в точке очередного приближения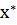 
должно выполняться условие 
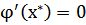. Решение данного уравнения ищут в виде 
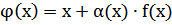, тогда:
В предположении, что точка приближения «достаточно близка» к корню, и что заданная функция непрерывна, окончательная формула такова:
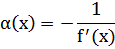
С учётом этого функция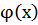 
определяется:
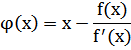
При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения f(x)=0 сводится к итерационной процедуре вычисления:
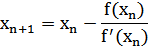
По теореме Банаха последовательность приближений стремится к корню уравнения f(x)=0
Метод секущих
Родственный метод секущих является «приближённым» методом Ньютона и позволяет не вычислять производную. Значение производной в итерационной формуле заменяется её оценкой по двум предыдущим точкам итераций:
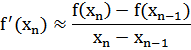
Таким образом, основная формула имеет вид
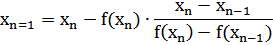
Этот метод по сравнению с методом Ньютона имеет меньшую скорость сходимости.
Лабораторная работа №1.
Реализовать один или несколько методов решения уравнений, заданных аналитически. Использовать средства ООП.