Методы приближенного решения уравнений. Метод последовательного поиска
Решаем приближенно уравнение F(x)=0 на отрезке [a,b] с точностью e. Пусть F(x) – непрерывная функция и на отрезке [a,b] выполняется достаточное условие существования корня 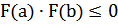 . Если
. Если 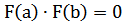 , то проверяем, какой из концов отрезка является корнем, в противном случае можно применить алгоритм последовательного поиска.
, то проверяем, какой из концов отрезка является корнем, в противном случае можно применить алгоритм последовательного поиска.
x=a; Fa=F(a);
do x=x+e; while F(x)*Fa>0;
Корнем объявляется x.
Методы приближенного решения уравнений. Метод вилки
Другое название метода – метод деления отрезка пополам. Решаем приближенно уравнение F(x)=0 на отрезке [a,b] с точностью e. Пусть F(x) – непрерывная функция и на отрезке [a,b] выполняется достаточное условие существования корня 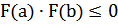 . Если
. Если 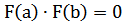 , то проверяем, какой из концов отрезка является корнем, в противном случае можно применить алгоритм деления отрезка пополам.
, то проверяем, какой из концов отрезка является корнем, в противном случае можно применить алгоритм деления отрезка пополам.
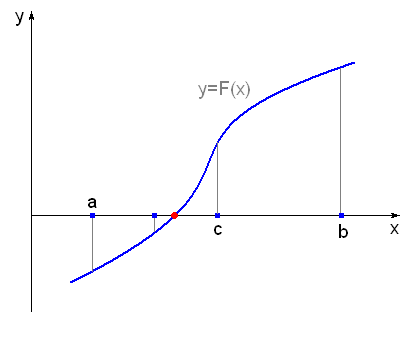
Суть алгоритма заключается в следующем. Из условия задачи мы уже имеем решение задачи с точностью 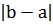 (в качестве решения можно взять любую точку отрезка [a,b], например точку a). Обозначим c=(a+b)/2 – середина отрезка [a,b], тогда возможны три варианта: либо F(c)=0 (тогда c – точное решение, в этом случае задача решена!), либо
(в качестве решения можно взять любую точку отрезка [a,b], например точку a). Обозначим c=(a+b)/2 – середина отрезка [a,b], тогда возможны три варианта: либо F(c)=0 (тогда c – точное решение, в этом случае задача решена!), либо 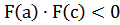 (тогда существует корень на отрезке [a,c], следовательно, мы имеем решение задачи с точностью
(тогда существует корень на отрезке [a,c], следовательно, мы имеем решение задачи с точностью 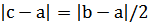 ), либо, наконец,
), либо, наконец, 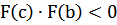 (тогда существует корень на отрезке [c,b], следовательно, мы получим решение задачи с точностью
(тогда существует корень на отрезке [c,b], следовательно, мы получим решение задачи с точностью 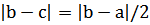 ).
).
Таким образом, алгоритм деления отрезка пополам позволяет за один шаг в два раза сократить область поиска решения уравнения. Применяя этот алгоритм 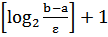 раз, получаем решение уравнения с точностью e.
раз, получаем решение уравнения с точностью e.
Методы приближенного решения уравнений. Метод простых итераций
Пусть 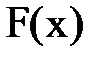 – непрерывная и дифференцируемая (гладкая) функция. Требуется решить на
– непрерывная и дифференцируемая (гладкая) функция. Требуется решить на 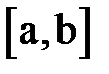 с точностью
с точностью 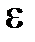 уравнение
уравнение 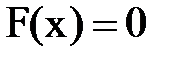 . Заменим исходное уравнение на эквивалентное (то есть полученное из исходного применением инвариантных преобразований)
. Заменим исходное уравнение на эквивалентное (то есть полученное из исходного применением инвариантных преобразований)
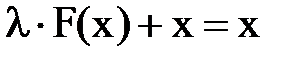 ,
,
где 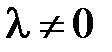 . Обозначим левую часть нового соотношения
. Обозначим левую часть нового соотношения 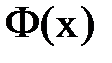 , тогда уравнение будет выглядеть так:
, тогда уравнение будет выглядеть так: 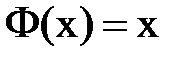 . Такая форма записи уравнения представляет собой итерационное соотношение. Возьмем наугад любое число из интервала
. Такая форма записи уравнения представляет собой итерационное соотношение. Возьмем наугад любое число из интервала 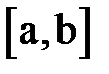 – x0. С помощью итерационного соотношения можно получить последовательность чисел x1=Ф(x0); x2=Ф(x1); x3=Ф(x2) … и т.д. Последовательность может сходиться или расходиться. Если процесс сходится, то, очевидно, предельное значение последовательности является решением уравнения. Если полученное решение принадлежит отрезку
– x0. С помощью итерационного соотношения можно получить последовательность чисел x1=Ф(x0); x2=Ф(x1); x3=Ф(x2) … и т.д. Последовательность может сходиться или расходиться. Если процесс сходится, то, очевидно, предельное значение последовательности является решением уравнения. Если полученное решение принадлежит отрезку 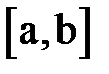 , то это искомое решение.
, то это искомое решение.
Добиться сходимости можно, если подобрать такое 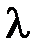 , чтобы для некоторого числа
, чтобы для некоторого числа 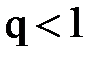 выполнялось неравенство
выполнялось неравенство 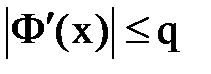 для всех x из
для всех x из 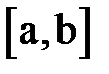 .
.
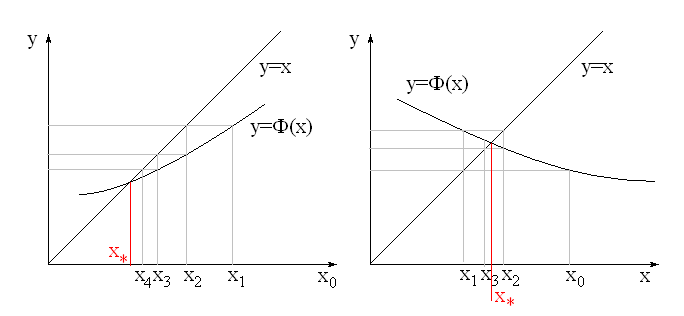
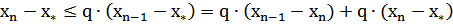
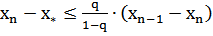
Требуемая точность будет достигнута, как только
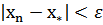
или
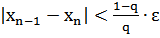 .
.








