Задача нахождения корня уравнения

Дата: 2025-05-25; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Лекция 2

Задача нахождения корня уравнения

Функция

X и Y – множества, функция f:XàY – алгоритм, сопоставляющий каждому элементу xÎX’ 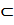X элемент из Y.

Множество X’ есть область определения функции.

Множество (область) значений Y’ является подмножеством Y.

Если конкретному элементу x*ÎX функция f сопоставляет элемент y*ÎY, то их связь обозначают y*=f(x*).

Принято саму функцию обозначать y=f(x), где x и y –некие абстрактные элементы X и Y. Далее будем считать, что X и Y являются подмножествами действительных чисел.

Уравнение

Соотношение y=f(x) рассматривается как уравнение относительно неизвестной величины x, если требуется найти такие значения аргумента функции x, что функция принимает заданное значение y. Более точно: даны y*ÎY и функция y=f(x), найти такое x*ÎX, что f(x*)=y*.

Для функций действительной переменной можно считать, что y*=0, поскольку вместо уравнения f(x)=y* можно рассматривать уравнение F(x)=0, где F(x)=f(x) –y*.

Решение уравнения

Пусть F(x) – непрерывная функция, F(x)=0 – уравнение. Тогда x* – корень (или решение) уравнения, если F(x*)=0.

Решить уравнение F(x)=0 на отрезке [a,b] означает – найти все корни на [a,b].

Условие 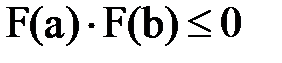является достаточным условием существования корня на [a,b], причем, если достигается точное равенство, то хотя бы один из концов отрезка является корнем уравнения.

Приближенное решение уравнения

Пусть x*– решение уравнения f(x)=0 на [a,b], x– приближенное решение f(x)=0 на [a,b] с точностью e, если x принадлежит [a,b] и 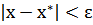. Одному точному решению соответствует много приближенных с точностью e решений.

Решить уравнение приближенно с точностью e на [a,b] – значит указать любое приближенное решение с точностью e на [a,b].

Методы точного решения уравнений

Для получения точного аналитического решения уравнения используют инвариантные алгебраические преобразования, которые меняют вид уравнения, но не изменяют решений. Примерами инвариантных преобразований могут служить операции добавления к обеим частям уравнения одной и той же величины, или же умножения левой и правой частей на одно и то же число, отличное от нуля.