Представление чисел в ЭВМ
Точные и приближённые методы решения (аналитические, численно-аналитические, численные методы).
Компьютерная реализация.
Действительные числа – конечное подмножество рациональных чисел
В компьютере действительное число
1 бит - знак числа, 8 бит - порядок, 23 биты – мантисса ( n =24)
Действительный 0. 0000 0000 0|000 0000 0000 0000 0000 0000
Действительная 1 0011 1111 1|000 0000 0000 0000 0000 0000
Действительная 2. 0100 0000 0|000 0000 0000 0000 0000 0000
Действительная 4. 0100 0000 1|000 0000 0000 0000 0000 0000
Действительная 8. 0100 0001 0|000 0000 0000 0000 0000 0000
Действительная -1. 1011 1111 1|000 0000 0000 0000 0000 0000
Действительная 10. 0100 0001 0|010 0000 0000 0000 0000 0000
Действительная 100. 0100 0010 1|100 1000 0000 0000 0000 0000
Мантисса (со слепой единицей) умножается на 2 в степени <показатель> - 1111111
Плотность расположения на действительной оси рациональных чисел, представляющих машинные действительные числа.
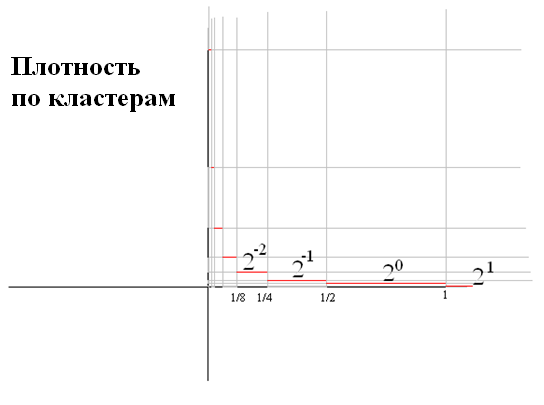
· Номер кластера – это величина порядка
· В каждом кластере 2n-1 штук чисел (мантисс).
· Плотность меньших чисел больше.
· Кластеры с меньшими числами имеют меньшую абсолютную погрешность
· Во всех кластерах (кроме самого левого и самого правого) относительные погрешности имеют одно и то же распределение (линейное от максимальной в левом конце до минимального в правом)
· При сложении (вычитании) двух чисел всегда теряются значащие цифры за счет того, что номер кластера суммы (разности) не совпадает с номером хотя бы одного из операндов
· При перемножении (делении) номера кластеров складываются (вычитаются)
· О величинах «порядка единицы». Чисел больших 1 и меньших 1 – одинаковое количество
Приближенные вычисления
Числа, заданные с погрешностью (или с заданной точностью)
Пример:
(И.С.Березин и Н.П.Жидков "Методы вычислений",в 2-х томах, М,"Физматгиз",1966, 464с,632с)
Вычислить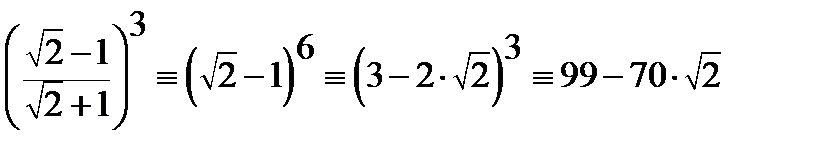 
Обозначим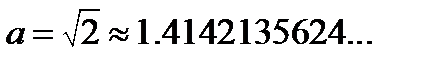 
Приближения:
1). 
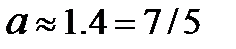- с точностью 0.02;
2) 
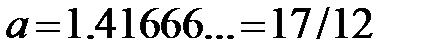с точностью 0.003
| 
| 
| 
|
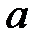
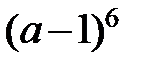
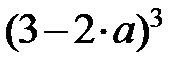
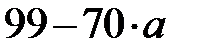
| 7/5 | 64/15625=0.004196.. | 1/125=0.008000 | 1.000 |
| 17/12 | 15625/2985354=0.005238 | 1/216=0.0046296 | -1/6=-0.1666... |
Выводы:
1. Ошибки переносятся и могут быть усилены.
2. Тождественные математические соотношения могут дать различные результаты.
3. Нужно уметь выбирать «лучшую» формулу.
Источники погрешностей
Конечность десятичного представления в ЭВМ.
Данные из эксперимента (систематические ошибки, случайные ошибки).
Итерационные методы вычислений.
Округления при выполнении арифметических действий.
Распространение ошибок в арифметических действиях.
Классификация погрешностей
Погрешность округления.
Неустранимая погрешность (определяется областью неопределенности).
Погрешность метода.
Терминология
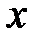- точное значение величины; 
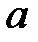- приближенное значение величины.
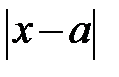- абсолютная погрешность; 
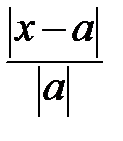- относительная погрешность.
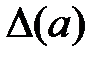- число, такое, что 
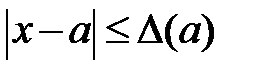- граница абсолютной погрешности.
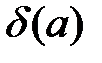- число, такое, что 
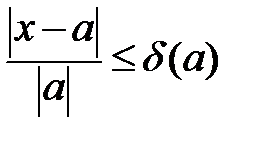- граница относительной погрешности.
x принадлежит интервалу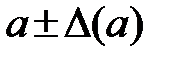 
или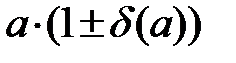 
;
Интервал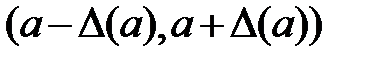 
- область неопределенности - неустранимая погрешность.
Если оказалось, что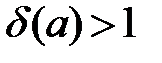 
, то говорят, что произошла потеря точности.
Машинный ноль - это минимальное число, которое ЭВМ отличает от нуля.
Исчезновение порядка - результат оказался меньше машинного нуля.
Переполнение арифметического устройства, или просто переполнение - результат больше (по модулю) максимального числа, которое может воспринимать ЭВМ.
Задача: Вычислить a*b/c, где a,b и c – «большие числа».
Распространение ошибок в арифметических операциях
Основные правила (неустранимая погрешность):
а).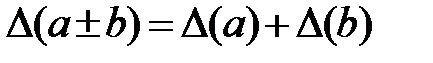 
а’)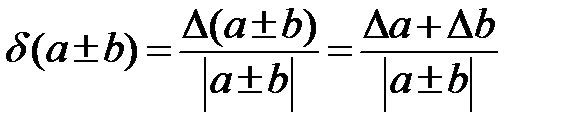 
б).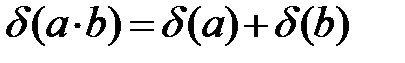 
(Почему?!)
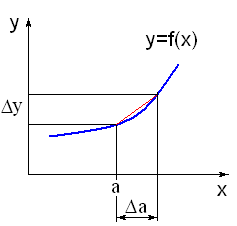
Интерпретация с площадями
в).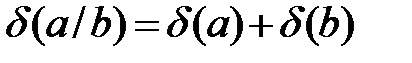 
г).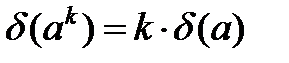 
д).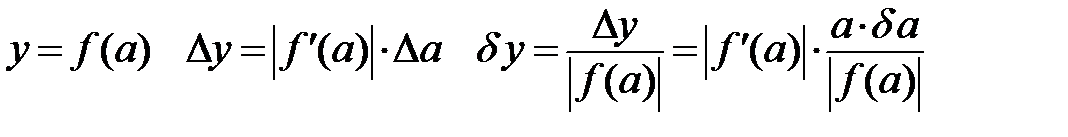 
Пример 1
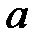=2520; 
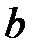=2518;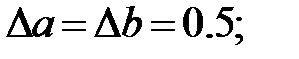 
Это означает, что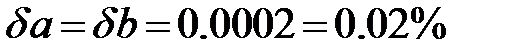 
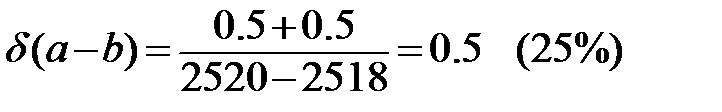
Пример 2
.
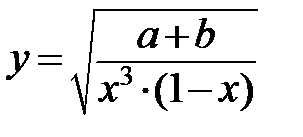Относительная погрешность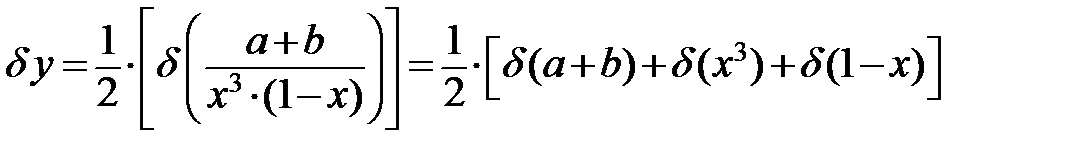 
=
= 
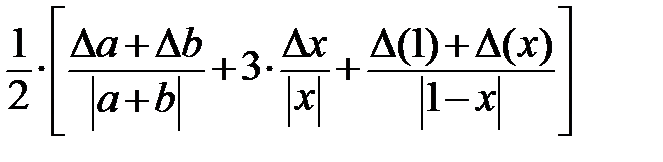
Объяснение примера п.3
= 
= 
= 
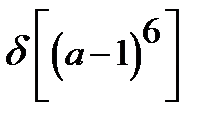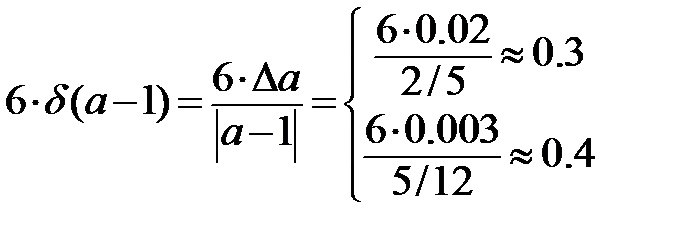
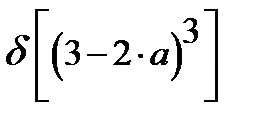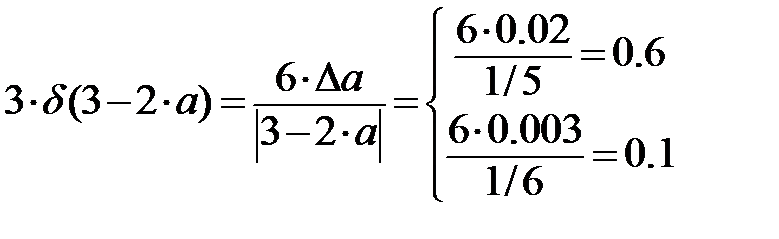
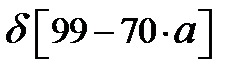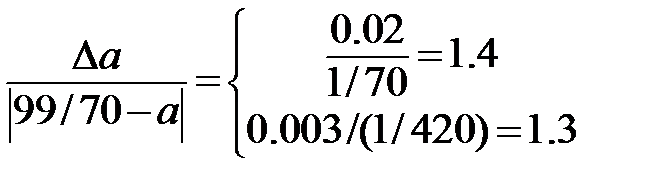
Задачи
Указать абсолютную и относительную погрешность, а также область неопределенности при округлении приближенных величин до 2 знаков после запятой:
1998.1998, 14.200009, 3.1415926, 0.0001
Получить относительные погрешности при вычислении значений арифметических выражений:
,
,
.
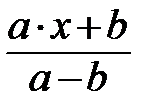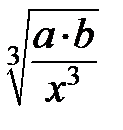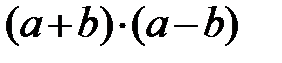Для всех переменных граница абсолютной погрешности задана величиной 0.01.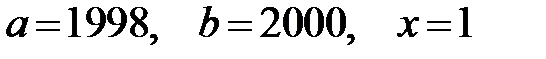 
Практические рекомендации.
Решение вычислительной задачи (вычисление определённого интеграла функции f(x))
Непрерывная функция заменяется дискретным аналогом (табуляция a,b,N,h).
Восстановление значения функции по таблице (интерполяция, k – порядок аппроксимации)
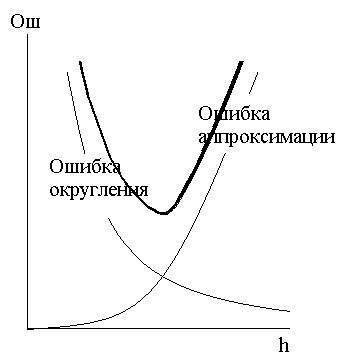
Ошибка восстановления пропорциональна hk.
Ошибка округления пропорциональна N.
Решение вычислительной задачи (вычисление определённого интеграла функции f(x))
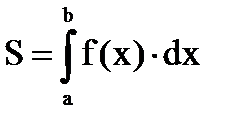
Функция табулируется с постоянным шагом h,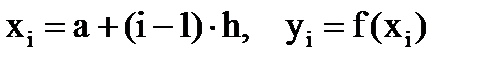 
| x | x1 | x2 | x3 | … | xn | xn+1 |
| y | y1 | y2 | y3 | … | yn | yn+1 |
Метод (формула) трапеций
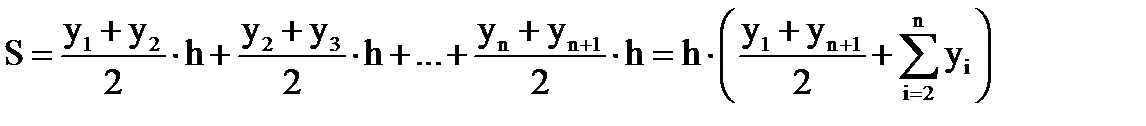
Ошибка O(h2), порядок аппроксимации 2.
Общая ошибка складывается из ошибки аппроксимации, пропорциональной h2, и ошибки округления, пропорциональной n, или 1/h. Существует оптимальный шаг дискретизации.
