Предмет «Вычислительная математика»
Лекция 1
Литература
1. Бабенко К. И. Основы численного анализа. –М.: Наука, 1986.
2. Бахвалов Н. С. Численные методы. 3-е изд. –М, 2003.
3. Демидович Б. П., Марон И. А. Основы вычислительной математики. — 2-е изд. –М.: Государственное издательство физико-математической литературы, 1963.
4. А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова. Вычислительные методы для инженеров. Учеб. пособие. –М.: Высш. Шк., 1994. – 544 с.: ил.
5. Мышенков В.И., Мышенков Е.В. Численные методы. Часть первая: Учебное пособие для студентов специальности 0101.07. – М.:МГУЛ,2001. – 120 с.: ил.
6. Мышенков В.И., Мышенков Е.В. Численные методы. Ч. 2. Численное решение обыкновенных дифференциальных уравнений: Учебное пособие для студентов специальности 073000. – М.:МГУЛ, 2005. – 109 с.: ил.
7. А.А.Самарский, А.В.Гулин. Численные методы. М.: «Наука», 1989.
8. И.С.Березин, Н.П.Жидков. Методы вычислений. Том 1. М., 1959.
9. Л.И.Турчак. Основы численных методов. М.: «Наука», 1987.
Содержание курса
· Предмет «Вычислительная математика»
· Математическое моделирование
· Представление чисел в ЭВМ
· Приближенные вычисления
· Методы решения уравнений
· Решение систем линейных алгебраических уравнений
· Табулирование, интерполяция, экстраполяция
· Аппроксимация экспериментальных данных
· Численное дифференцирование
· Численное решения обыкновенных дифференциальных уравнений
· Численное решение дифференциальных уравнений в частных производных
· Задачи вычислительной гидродинамики
· Другие задачи вычислительной математики
Предмет «Вычислительная математика»
Прикладная математика – область математики, рассматривающая применение математических методов и алгоритмов в других областях науки и практики.
· Вычислительная математика (численные методы)
· Дискретная математика (комбинаторика, конечная математика)
· Теория алгоритмов (скалярные, параллельные, распределённые и облачные вычисления)
· Теория приближённых вычислений
· Математическая физика (механика сплошных сред)
· Математическое программирование (линейное программирование)
· Оптимизация
· Теория массового обслуживания
· Исследование операций (теория игр)
· Теория информации (информатика, криптография, защита информации)
· Теория вероятностей и математическая статистика
· Экономическая математика (финансовая математика)
· Биоматематика (биоинформатика)
· И др.
Вычислительная математика – раздел математики, включающий круг вопросов, связанных с производством разнообразных вычислений. В более узком понимании вычислительная математика – теория численных методов решения типовых математических задач. Современная вычислительная математика включает в круг своих проблем изучение особенностей вычисления с применением компьютеров.
Математическое моделирование
Объект исследования - это реальный объект, поведение или свойства которого изучаются методами математического моделирования. На первом этапе изучения (рис.1.) объект исследования заменяется некоторым абстрактным объектом, называемым расчетной схемой.
Расчетная схема сохраняет все элементы и свойства реального объекта, которые по мнению исследователя (разработчика математической модели) являются существенными и качественно определяют взаимосвязи между элементами реального объекта.
Математическая модель количественно описывает взаимосвязи между отдельными элементами расчетной схемы. При разрешении математических соотношений используют различные методы - точные или приближенные.
Алгоритм - это предписание, указывающее на то, какие именно действия и в какой последовательности следует выполнять при разрешении математических соотношений с использованием данного метода.
Реализация - процесс получения конкретных результатов на основе данной математической модели с использованием данного метода по данному алгоритму. Как правило, полученный результат не является конечной целью исследования.
Дальнейшие наблюдения за объектом, сопоставление полученных на основе данной математической модели характеристик свойств и поведения объекта, возрастающие потребности в точности данных и т.п., заставляют исследователя вернуться к началу исследовательского цикла и повторить весь процесс (уточнение расчетной схемы, построение математической модели, выбор метода и алгоритма, реализация).
| Объект исследования |
| Расчетная схема |
| Математич.модель |
| Алгоритм, метод |
| Реализация |
| Анализ, уточнения, учет других факторов |
Рис. 1.
Пример 1
Модель поверхности крышки стола
1. Плоскость прямоугольной формы
2. Плоскость, ограниченная четырехугольником
3. Поверхность, ограниченная четырехугольником
4. А закругленные края?
Пример 2
Объект исследования.
Движение тела, брошенного со скоростью v0 под углом 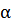 к поверхности Земли.
к поверхности Земли.
Расчетная схема.
Движение тела характеризуется зависимостью вертикальной (y) и горизонтальной (x) координатами от времени (t)
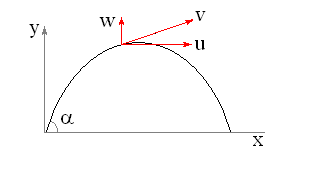
Рис. 1. Расчетная схема
Математическая модель.
Горизонтальная составляющая скорости постоянна 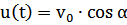 .
.
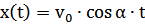 .
.
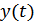 можно получить из системы
можно получить из системы
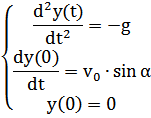
Модель полна и непротиворечива.
Решение задачи получается аналитически.
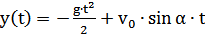 , (1)
, (1)
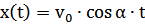 . (2)
. (2)
Реализация.
Момент падения тела на поверхность Земли определяется из квадратного уравнения
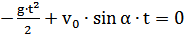 ,
,
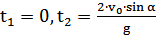 .
.
С помощью формул (1) и (2) можно определить положение тела в любой момент в диапазоне времени полета.
Анализ.
Учесть, например, сопротивление воздуха.
g - ускорение силы тяжести - параметр модели,
t - модельное время,
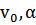 - входные данные,
- входные данные,
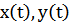 - выходные данные.
- выходные данные.
В данной формулировке это прямая задача.
Обратная задача - по траектории определить 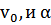 .
.
Задача идентификации - по известной траектории и известным параметрам 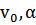 определить g (на какой планете бросали тело?).
определить g (на какой планете бросали тело?).
Статическая модель (Пример 1), динамическая модель (Пример 2)
Имитационная модель - функционирование объекта воспроизводится в соответствии с течением модельного времени.
Вычислительный эксперимент.








