Всероссийская студенческая олимпиада (Московский тур)
по физике (в технических вузах)
2014 г.
II тур Всероссийской физической олимпиады студентов технических вузов прошел 5 апреля 2014 года в Московском государственном техническом университете (МГТУ) им. Н.Э. Баумана.
Победители в командном зачете: команда Московского государственного технического университета им. Н.Э. Баумана, набравшая 194 балла - первое место, команда Российского государственного университета нефти и газа имени И.М. Губкина, набравшая 129 баллов - второе место, команда Калужского филиала Московского государственного технического университета им. Н.Э. Баумана, набравшая 114 баллов - третье место.
Победители в личном зачете: Бланк Сергей Сергеевич МГТУ им. Н.Э. Баумана - первое место, Шибаев Максим Игоревич МГТУ им. Н.Э. Баумана - второе место, Рогожинский Константин Сергеевич МГТУ им. Н.Э. Баумана - третье место.
Задачи олимпиады
Задача 1. Горизонтально расположенный резиновый шнур правым концом закреплен на стенке, а левый конец тянут в горизонтальном направлении налево с постоянной скоростью V. Жук ползет по шнуру от стенки к левому концу с постоянной скоростью U. Определить максимальное расстояние между правым концом шнура и жуком в процессе дальнейшего движения при V > U. Начальная длина шнура равна l.
Задача 2. Санки длины l съехали с горки по снегу и, разогнавшись до скорости равной V 0, въехали на горизонтальный участок с асфальтом. Определить путь, который пройдут санки по асфальту до полной остановки, если коэффициент трения санок с асфальтом равен k.
Задача 3. Космическая станция движется по стационарной круговой орбите радиуса R вокруг Земли. Станция представляет собой два шара массы m радиуса r, соединенных жестким стержнем длины L (r << L << R). Определить угловую скорость w о станции вокруг оси вращения, совпадающей с жестким стержнем, необходимую для того, чтобы угол между радиус-вектором станции, проведенным от центра Земли, и осью вращения станции был равен α и оставался постоянным. Учесть изменение силы тяжести на расстоянии L.
Задача 4. Поршень площадью S массой M лежит на дне вертикально расположенного цилиндра, верхний конец которого открыт в атмосферу. Через небольшое отверстие в дне цилиндра медленно под поршень закачивают воздух из атмосферы до тех пор, пока поршень не поднимется на величину h. Определить затраченную работу, считая, что процесс изотермический.
Задача 5. Металлический полуцилиндр радиуса R длины L >> R, образованный секущей плоскостью проходящей через его ось, заряжен зарядом Q. Основание этого полуцилиндра закрыто диэлектрической пластиной длины L ширины 2 R, заряженной равномерно по поверхности зарядом q. Определить силу взаимодействия между пластиной и полуцилиндром.
Задача 6. По полубесконечному цилиндрическому соленоиду радиуса R с плотностью намотки n протекает ток I. Определить поток магнитного поля, пронизывающего кольцо радиуса 2 R лежащего в плоскости среза, центр которого совпадает с осью цилиндра.
Задача 7. Две плоские гармонические электромагнитные волны интенсивности I 0 распространяются в вакууме: первая вдоль оси x, вторая вдоль y. Векторы напряженности E обеих волн колеблются вдоль оси z . Построить годограф вектора Пойнтинга S в точке, где разность фаз между волнами равна 
.
Решение
Решение задачи 1. Пусть x - координата жука, а X - координата левого конца шнура. Скорость жука в неподвижной системе координат -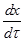 
. Координата левого конца шнура X = l + Vτ . Скорость точки шнура, в которой на данный момент находится жук - 
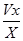. Тогда 
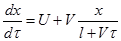. Это уравнение решается - 
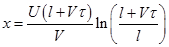. Скорость жука в неподвижной системе отсчета в момент максимального расстояния равна скорости левого конца жгута - 
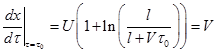. Откуда время, когда расстояние максимально - 
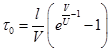. Максимальное расстояние - 
.
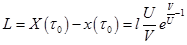Ответ: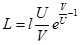 
.
Решение задачи 2. Пусть x координата «носа» саней. Считаем, что сила трения F пропорциональна части длины саней, заехавших на асфальт -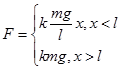 
. Из теоремы об изменении механической энергии системы - 
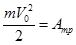. Если до остановки санки не заехали полностью на асфальт - 
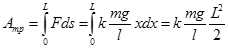и 
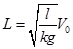. Если до остановки санки полностью заехали на асфальт - 
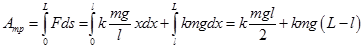и 
.
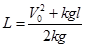Ответ: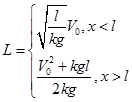 
.
Решение задачи 3. Разность сил тяжести действующих на шары массой m -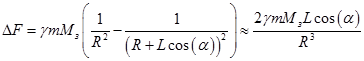 
. Момент силы тяжести, приложенный к станции, стремящийся вернуть её в устойчивое состояние вызывает прецессию с угловой скоростью ω p, равной угловой скорости вращения вокруг Земли ω. Из второго закона Ньютона - 
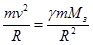, а v =ω R. Следовательно - 
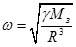. Момент импульса станции 
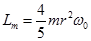. Пользуясь уравнением динамики вращательного движения, получаем - 
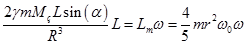. Выражая из него угловую скорость вращения получаем - 
.
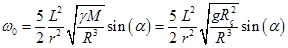Ответ: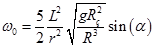 
Решение задачи 4. Объём воздуха V 0 массы m давлением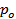 
в начальный момент находился вне цилиндра. После поступления в цилиндр, будет иметь объём внутри поршня V = Sh давлением pk = p 0 + Mg / S. Сначала объем воздуха сжимается от давления p 0 до pk, откуда работа 
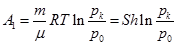. Потом воздух закачивается под поршень 
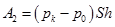. Полная работа будет 
.
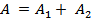Ответ: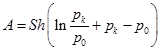 
.
Решение задачи 5. Разобьем поверхность цилиндра на площадки dl × L. Заряд на этих площадках dQ создает поток через основание цилиндра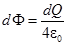 
вне зависимости от положения площадки. 
.
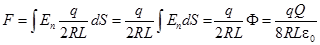Ответ: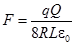 
.
Решение задачи 6. Дополним полубесконечный соленоид симметричным до бесконечного. Поток через срез бесконечного соленоида равен Ф1=π R 2 µ0 nI. В силу симметрии поток через полубесконечный соленоид Ф=π R 2 µ0 nI /2. Силовая линия, сходящая с края полубесконечного соленоида, лежит в плоскости среза, т.к. поле вне бесконечного соленоида равно нулю и является суперпозицией полей от двух симметричных полубесконечных соленоидов. Поток через кольцо равен Ф.
Ответ: Ф=π R 2 µ0 nI /2.
Решение задачи 7. Интенсивность волны для гармонических колебаний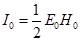 
. Колебания в точке 
, 
, 
, 
.
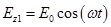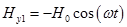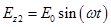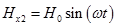Найдем проекции вектора S на оси координат: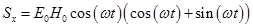 
, 
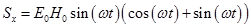. Для удобства, введем обозначение: 
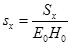и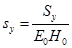 
. Тогда, проделывая математические преобразования, можно показать 
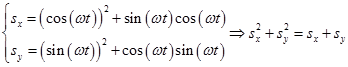. Откуда 
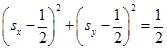. Получили уравнение смещенной окружности.
Ответ: Годограф представляет собой окружность, 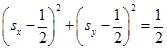.