Всероссийская студенческая олимпиада (Всероссийский тур)
по физике (в технических вузах)
2014 г.
III тур Всероссийской физической олимпиады студентов технических вузов прошел 15 мая 2014 года в Московском государственном техническом университете (МГТУ) им. Н.Э. Баумана.
Победители в командном зачете: команда Санкт-Петербургского государственного политехнического университета, набравшая 125 баллов - первое место, команда Московского государственного технического университета им Н.Э. Баумана, набравшая 94 балла - второе место, команда Московского авиационного института, набравшая 50 баллов - третье место.
Победители в личном зачете: Соболев Антон Игоревич, СПб ПТУ – первое место, Авдеев Иван Дмитриевич, СПб ПТУ – второе место, Шибаев Максим Игоревич, МГТУ им. Н.Э. Баумана - третье место.
Задачи олимпиады
Задача 1. Автомобиль движется по ровной горизонтальной поверхности, коэффициент трения с которой равен k. Автомобиль должен совершить поворот на 90° градусов за минимально возможное время. Считая, что начало маневра совпало с началом координат, а ось y направлена по вектору скорости, величина которой в начале и конце поворота равна V, определить траекторию движения за время совершения маневра.
Задача 2. Тонкая нерастяжимая и абсолютно гладкая нить закреплена на потолке в точках A и B, расстояние между которыми равно a. Длина нити l =2 a. Из точки A начинает скользить маленькое кольцо, в которое продета нить. Определить скорость кольца сразу после натяжения нити.
Задача 3. На длинных невесомых нитях, касаясь друг друга, подвешена очень длинная цепочка шариков одинакового диаметра, масса которых убывает, образуя прогрессию. Определить эту прогрессию, если известно, что когда первому шарику ударом придают скорость V0, вся цепочка, кроме последнего шарика, после серии абсолютно упругих соударений начинает двигаться как единое целое со скоростью V0/2.
Задача 4. Определить период колебаний треугольника, состоящего из трех стержней одинаковой массы, относительно оси перпендикулярной плоскости треугольника и проходящей через вершину O, в которой сходятся стержни a и b. Длина и ориентация этих стержней задана векторами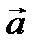 
и 
.
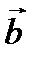Задача 5. Нагретый у поверхности Земли в экваториальной части воздух поднимается в верхние слои атмосферы, и впоследствии опускается к поверхности Земли в полярных областях. Принимая, что воздух, поднимаясь в верхние слои атмосферы или опускаясь вниз, расширяется или сжимается адиабатически, определить изменение температуры воздуха с высотой T ( z ), считая, что на поверхности Земли температура равна T 0.
Задача 6. Диэлектрическая поверхность в форме куба с ребром l заряжена равномерно по поверхности поверхностной плотностью заряда s. Определить силу, действующую на грань куба.
Задача 7. Заряженная частица с зарядом q массой m движется co скоростью V в магнитном поле диполя в плоскости, перпендикулярной оси диполя. Магнитное поле диполя меняется по закону B = a / r 3. Определить минимальное расстояние, на которое может приблизиться частица к диполю, если она начинает движение из бесконечно удаленной точки в направлении к диполю строго вдоль радиус-вектора r.
Задача 8. Заряд q массой m движется по замкнутой траектории под действием постоянного однородного магнитного поля с индукцией B, направленного по оси y и переменного электрического поля E = E 0 cos ( ωt ), направленного по оси z. При каких условиях движение заряда будет периодическим с круговой частотой, совпадающей с круговой частотой изменения электрического поля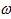 
. Определить зависимости от времени проекций Vz и Vx скорости заряда. Какова будет при этом траектория движения заряда.
Решения
Решение задачи 1. Изменение вектора скорости за время поворота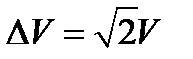 
под углом 45 градусов навстречу движению. Ускорение a = kg, сонаправлено с Δ V, 
, 
, 
, 
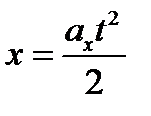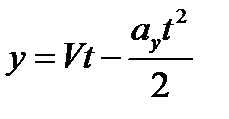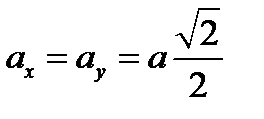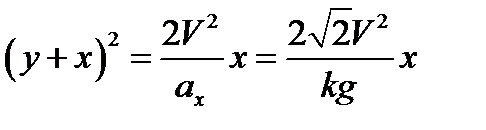- траектория - парабола.
Ответ: Парабола,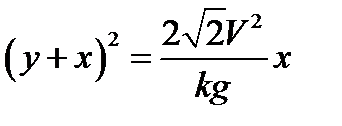 
.
Решение задачи 2. До натяжения нити кольцо будет падать вертикально, натяжение произойдет в точке C в момент, когда кольцо упадет на Y =3a/4,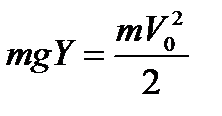 
, 
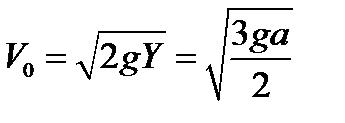. Силы натяжения нити слева и справа от колечка в момент удара равны из-за гладкости нити. Следовательно, результирующая сила направлена по биссектрисе угла между нитями. Проекция скорости на биссектрису при ударе обнуляется. Вектор скорости после удара будет перпендикулярен биссектрисе. 
.
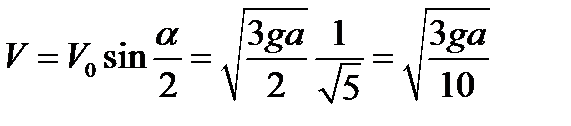Ответ: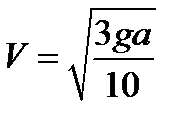 
.
Решение задачи 3. Пусть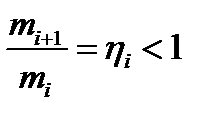 
. Уравнения удара между i и (i +1) шаром 
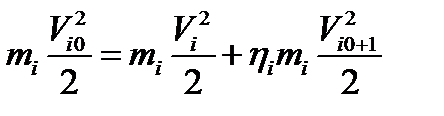и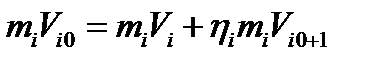 
, где Vi 0 – скорость бьющего шара до, а Vi – после удара. Далее 
, 
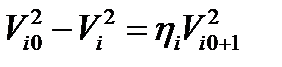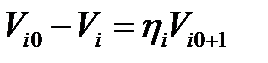, откуда 
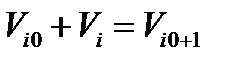. Пусть 
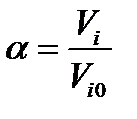, тогда 
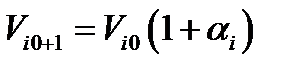и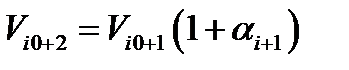 
. Из условия задачи 
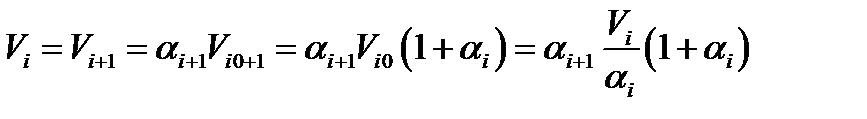, откуда 
, 
, 
, 
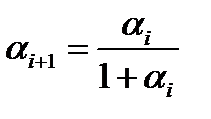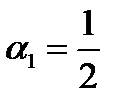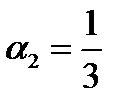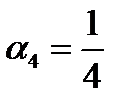и т.д. 
. 
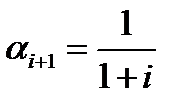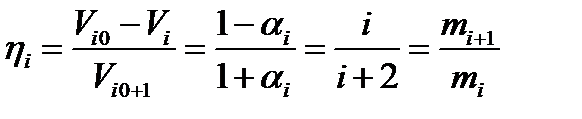. Откуда 
.
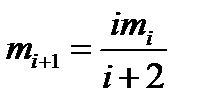Ответ: .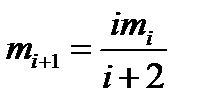
Решение задачи 4. Вектор проведенный из точки О в центр масс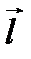 
. 
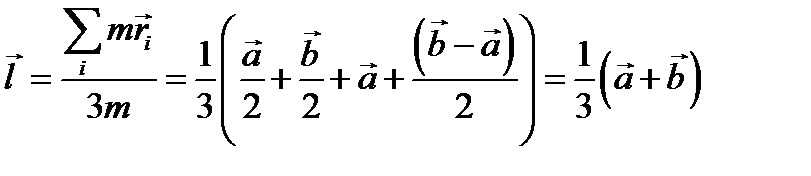. Момент инерции
.
.
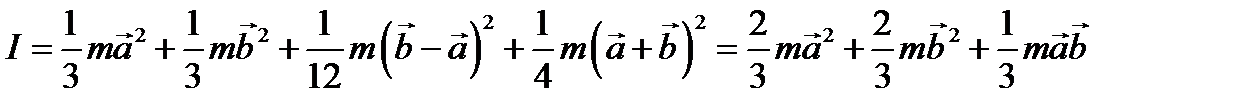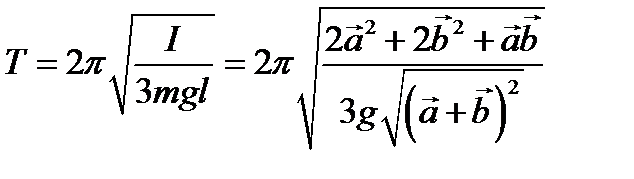Ответ: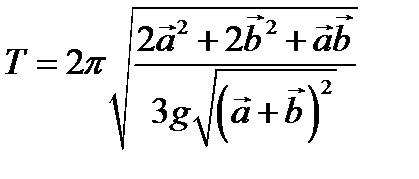 
.
Решение задачи 5. Барометрическое соотношение: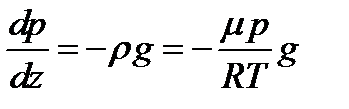 
. Уравнение адиабаты: 
, 
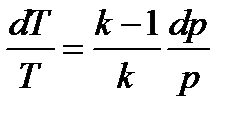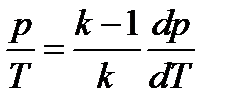. Откуда 
, 
, 
, 
. 
.
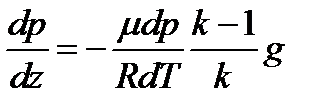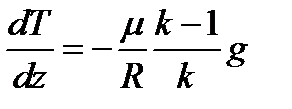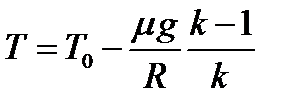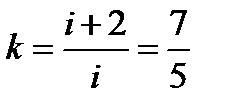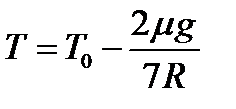Откуда: .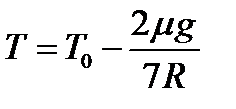
Решение задачи 6. Общий заряд на поверхности равен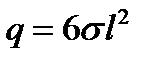 
. Нормальная составляющая силы, действующая на плоскую пластину площадью S, заряженную равномерно поверхностной плотностью заряда σ равна: 
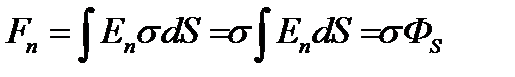, где Ф S - поток вектора напряженности электрического поля через поверхность S. Половина потока 
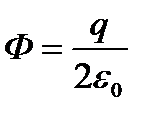направлена внутрь куба, а половина вне. Тот поток, который направлен внутрь, вытекает через поверхность, равномерно распределяясь между шестью гранями. Откуда 
.
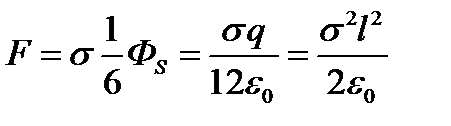Ответ: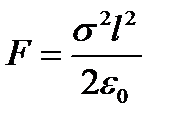 
.
Решение задачи 7. Величина скорости остается постоянной, меняется направление скорости и момент импульса.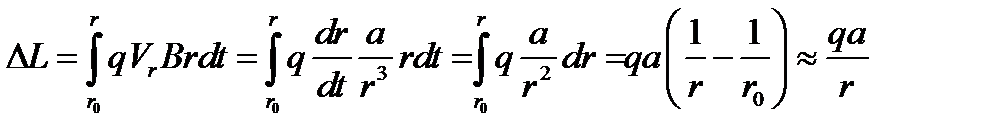 
. Чем больше изменение момента импульса Δ L, тем ближе приблизится частица к диполю. Следовательно, начальный момент импульса L 1 =0 в процессе движения уменьшается и достигает в ближайшей к диполю точке значения L 2 =- mVr, 
, 
.
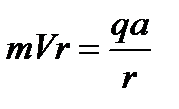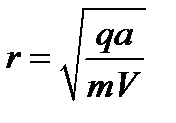Ответ: .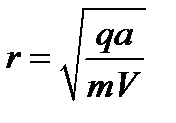
Решение задачи 8.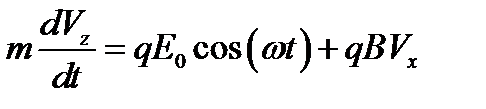 
, 
, 
, 
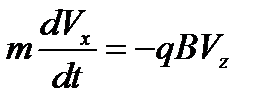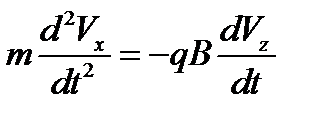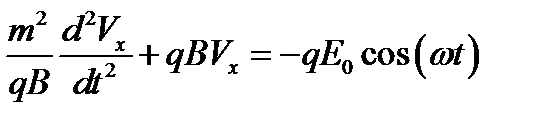. Решение ищем в виде 
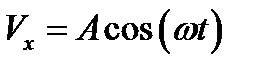, так как собственное движение с циклотронной частотой 
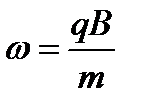отсутствует.
, 
, 
.
, 
.
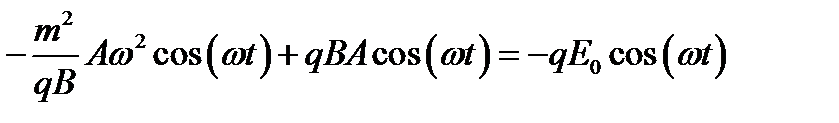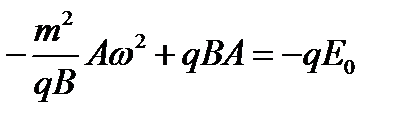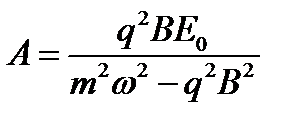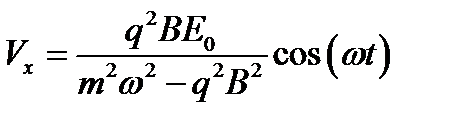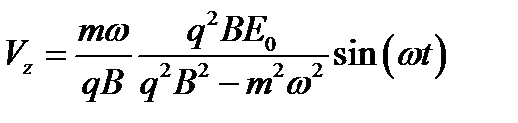Ответ: При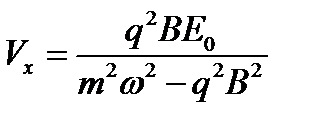 
, Vz =0, траектория эллипс.