Исследование колебательного звена
Передаточная функция колебательного звена имеет вид: W(S)=k/1+2ST+T^2S^2
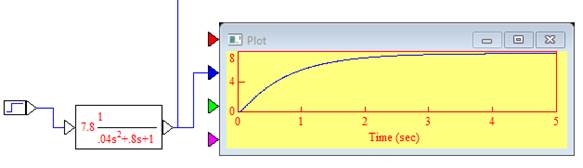
Построить переходную характеристику колебательного звена для k =7.8; Т =1, 0.2 и 5.0, при изменении затухания z от 0.25 до 2.0.
Оценить влияние изменения параметров передаточной функции колебательного звена на вид и длительность его переходной характеристики.
Открыть новую диаграмму VisSim.
Поместить в рабочее пространство Vissim следующие блоки:
генератор ступенчатого единичного воздействия 1(t): Blocks → Signal Producer → step;
блок линейной системы, или линейный блок, описываемый передаточной функцией W(s): Blocks → Linear System → Transfer Function;
• осциллограф: Blocks → Signal Consumer → plot.
Подключить step к входу блока Transfer Function, а его выход к входу осциллографа plot.
Настроить линейный блок: дважды щелкнуть по блоку левой кнопкой мыши или один раз правой. В появившемся окне установить: усиление (Gain) равным 7.8, числитель (Numerator) оставить равным 1, для знаменателя (Denominator) в случае, когда Т=0.2 и z=2 набрать 0.04 (пробел) 0.8 (пробел) 1. Символы "s2" и "+", а также "s" и "+" в знаменателе не указываются, они по принятому в VisSim соглашению заменяются при вводе пробелами. Нажать ОК.
Звено запаздывания
Это звено часто встречается в моделях реальных систем и зачастую его присутствие ухудшает свойства системы по сравнению с тем, как если бы его не было. Поэтому, если в реальной системе имеется такой элемент, то для обеспечения адекватности модели важно ввести его и в модель.
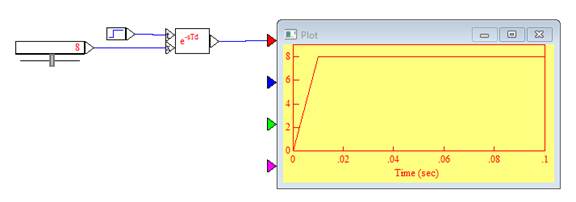
1. Поместить в новое рабочее пространство блок задержки: Blocks → Time Delay → timeDelay.
2. Поместить слайдер, генератор ступеньки и осциллограф. На вход х блока задержки подать ступеньку, на вход t подключить слайдер (полосу прокрутки числовых значений) и выход блока подключить к осциллографу.
3. Изменяя задержку и запуская на счет посмотреть осциллограммы.
ЛАБОРАТОРНАЯ РАБОТА № 3
Апериодическое звено
Построить в среде VisSim, проанализировать и распечатать ЛАЧХ и ЛФЧХ апериодического звена.
1. Открыть диаграмму с исследованием апериодического звена из предыдущей лабораторной работы.
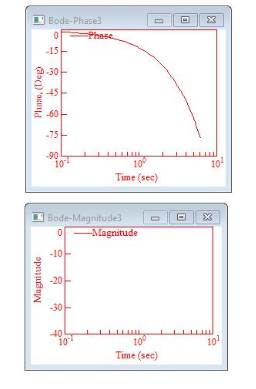
Примечание. Выделить блок апериодического звена, нажав левую кнопку мыши за его пределами и расширив рамку до включения в нее блока. Отпустить кнопку. Блок станет черным. В меню: Analyze → Frequecy Response. На рабочем пространстве появятся два графика, представляющие собой ЛАЧХ и ЛФЧХ. Растянуть их и поместить в правой части экрана друг под другом. Ввести сетку координат: plot → двойной щелчок → Grid Lines – установить флажок. Нажать OK. На верхнем графике, ЛАЧХ, установить по оси ординат значение в децибелах.
2. Для нижнего графика, ЛФЧХ установить значение Y Lower Bound равным -90 градусов. Поставить флажок Fixed Number of Divisions, установить значение Y Divisions равным 6. Нажать OK.
3. Сделать подписи графиков, кривых, осей. Установить белый цвет фона. Сохранение.
Диаграмму в VisSim можно сохранить (в View → Display Mode) и как картинку с расширением .wmf, а затем распечатать.
Колебательное звено
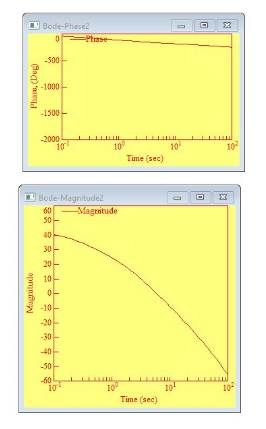
1. Открыть диаграмму с исследованием колебательного звена из предыдущей лабораторной работы.
2. Построить ЛАЧХ и ЛФЧХ для T =1, k=1 и z= 0.25; 0.5; 0.707, 1.0; и для 2.0.
ЛАБОРАТОРНАЯ РАБОТА № 4
Линейные системы, содержащие контур из устойчивых звеньев могут быть неустойчивыми. В системах управления неустойчивость, как правило, является недопустимой, вредной. В системах генерации неустойчивость напротив, необходима.
Определение: по Ляпунову система устойчива, если по окончании воздействия она возвращается в исходное состояние.
Существуют т.н. критерии устойчивости – правила, позволяющие узнать, будет ли система устойчивой или нет по ее модели. Критерии бывают алгебраические (Гурвица, Рауса) и частотные (Михайлова, Найквиста).
По критерию Найквиста для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф комплексного коэффициента передачи разомкнутого контура не охватывал на комплексной плоскости точку с координатами (-1, j0). При этом необходимо, чтобы разомкнутый контур был устойчив.
В логарифмическом варианте формулировки критерия Найквиста для устойчивости системы необходимо и достаточно чтобы частота среза wср была меньше частоты wp.
Для получения системы управления хорошего или, по крайней мере, удовлетворительного качества, необходимо выполнить три условия:
· запас g устойчивости по фазе должен составлять 350..650 и более;
· запас L устойчивости по амплитуде должен быть 6..12..20 дБ и более;
· если система статическая, то усиление ее контура должно находиться в пределах 20..40 дБ.
Задание к работе
.








