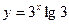[q]3:1: Составить уравнение плоскости, которая проходит через точку параллельно плоскости Oxy
[a] z+3=0
[a] x-3=0
[a] 4x-z=0
[a] z-3=0
[a] z=0
[q]3:1: Составить уравнение плоскости, которая проходит через точку 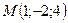 параллельно плоскости Oxz
параллельно плоскости Oxz
[a] x=0
[a] z=2
[a] 5z-2=0
[a] y=-2
[a] x-y=0
[q]3:1: Найти точку пересечения плоскости 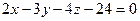 с осью ОХ
с осью ОХ
[a] (0;6;0)
[a] (4;0;9)
[a] (-8;4;0)
[a] (14;0;0)
[a] (12;0;0)
[q]3:1: Найти точку пересечения плоскости 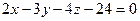 с осью ОУ
с осью ОУ
[a] (4;0;9)
[a] (-8;4;0)
[a] (0;-8;0)
[a] (0;6;0)
[a] (14;0;0)
[q]3:1: Найти точку пересечения плоскости 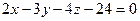 с осью ОZ
с осью ОZ
[a] (4;0;9)
[a] (-8;4;0)
[a] (0;0;-6)
[a] (0;6;0)
[a] (14;0;0)
[q]3:1: Дано уравнение плоскости 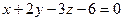 . Написать для нее уравнение в "отрезках" на осях координат
. Написать для нее уравнение в "отрезках" на осях координат
[a] 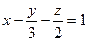
[a] 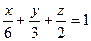
[a] 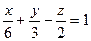
[a] 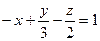
[a] 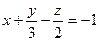
[q]3:1: Найдите острый угол между прямыми 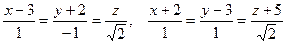
[a] 450
[a] 300
[a] 900
[a] 00
[a] 600
[q]3:1: Составить уравнение сферы, если имеет центр (0;0;0) и радиус r = 8
[a] х2 +у2 +z2=0
[a] х2 +у2 +z2=8
[a] х2 +у2 +z2=-64
[a] х2 +у2 +z2=16
[a] х2 +у2 +z2=64
[q]3:1: Составить уравнение сферы, если имеет центр (0;0;0) и радиус r = 2
[a] х2 +у2 +z2=0
[a] х2 +у2 +z2=8
[a] х2 +у2 +z2=-6
[a] х2 +у2 +z2=16
[a] х2 +у2 +z2=4
[q]3:1: Каноническое уравнение эллипса имеет вид
[a] 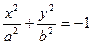
[a] 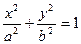
[a] 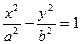
[a] 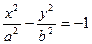
[a] 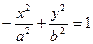
[q]3:1: Каноническое уравнение гиперболы имеет вид
[a] 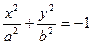
[a] 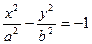
[a] 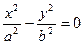
[a] 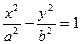
[a] 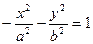
[q]3:1: Каноническое уравнение параболы имеет вид
[a] 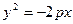
[a] 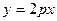
[a] 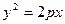
[a] 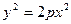
[a] 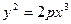
q]3:1: Каноническое уравнение трехосного эллипсоида имеет вид
[a] 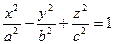
[a] 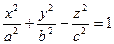
[a] 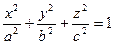
[a] 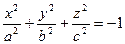
[a] - 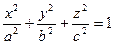
[q]3:1: Каноническое уравнение гиперболического параболоида имеет вид
[a] 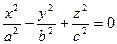
[a] 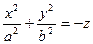
[a] 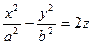
[a] 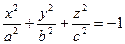
[a] - 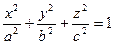
[q]3:1: Каноническое уравнение однополостного гиперболоида имеет вид
[a] 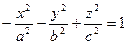
[a] 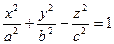
[a] 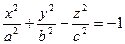
[a] 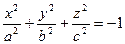
[a] - 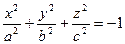
q]3:1: Каноническое уравнение двуполостного гиперболоида имеет вид
[a] 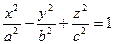
[a] 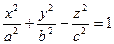
[a] 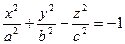
[a] 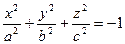
[a] - 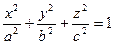
[q]3:1: Вычислить определитель 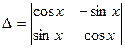
[a] 5
[a] 4
[a] 3
[a] 1
[a] 0
[q]3:1: Вычислить определитель 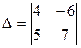
[a] 0
[a] 17
[a] 52
[a] 90
[a] 58
[q]3:1: Вычислить определитель 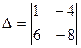
[a] 16
[a] -16
[a] 32
[a] -32
[a] 0
[q]3:1: Вычислить определитель 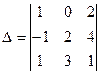
[a] 18
[a] 20
[a] 5
[a] 30
[a] -20
[q]3:1: Вычислить определитель 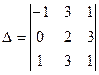
[a] 14
[a] 10
[a] 20
[a] 6
[a] 5
[q]3:1: Вычислить определитель 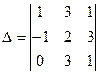
[a] 0
[a] 4
[a] -6
[a] 2
[a] -7
[q]3:1: Вычислить определитель 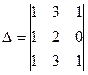
[a] 0
[a] 1
[a] 2
[a] -1
[a] -2
[q]3:1: Вычислить определитель 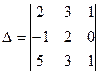
[a] -6
[a] 1
[a] 5
[a] 9
[a] 0
[q]3:1: Вычислить определитель 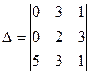
[a] 28
[a] 61
[a] -32
[a] 0
[a] 35
[q]3:1: Найти А+В, если 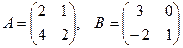
[a] 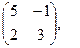
[a] 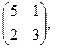
[a] 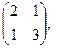
[a] 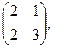
[a] 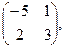
[q]3:1: Найти А-В , если 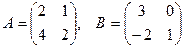
[a] 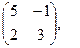
[a] 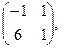
[a] 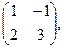
[a] 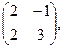
[a] 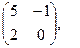
[q]3:1: Найти А+В, если 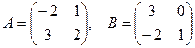
[a] 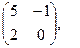
[a] 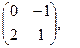
[a] 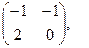
[a] 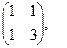
[a] 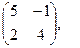
[q]3:1: Найти А-В, если 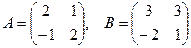
[a] 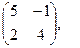
[a] 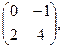
[a] 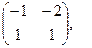
[a] 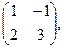
[a] 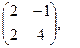
[q]3:1: Найти А*В , если 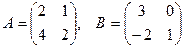
[a] 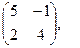
[a] 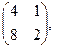
[a] 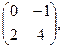
[a] 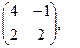
[a] 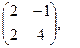
[q]3:1: Найти А*В , если 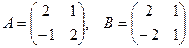
[a] 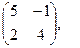
[a] 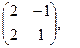
[a] 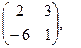
[a] 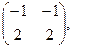
[a] 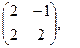
[q]3:1: Найти А*В , если 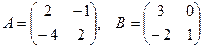
[a] 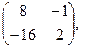
[a] 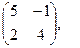
[a] 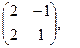
[a] 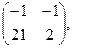
[a] 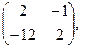
[q]3:1: Найти А+4В, если 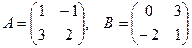
[a] 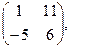
[a] 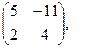
[a] 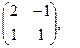
[a] 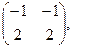
[a] 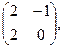
[q]3:1: Найти А+2В, если 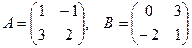
[a] 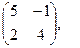
[a] 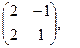
[a] 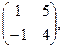
[a] 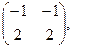
[a] 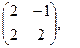
[q]3:1: Найти 2 А-В, если 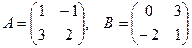
[a] 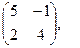
[a] 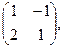
[a] 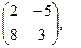
[a] 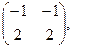
[a] 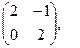
[q]3:1: Найти А-2В, если 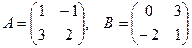
[a] 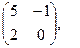
[a] 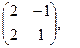
[a] 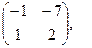
[a] 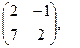
[a] 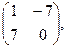
[q]3:1: Найти 2А+В, если 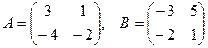
[a] 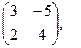
[a] 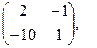
[a] 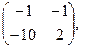
[a] 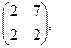
[a] 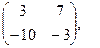
[q]3:1: Найти А-3В, если 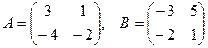
[a] 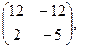
[a] 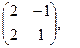
[a] 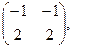
[a] 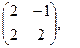
[a] 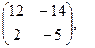
[q]3:1: Найти А*В , если 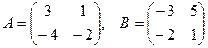
[a] 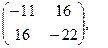
[a] 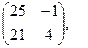
[a] 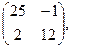
[a] 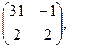
[a] 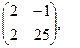
[q]3:1: Найти А+В, если 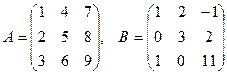
[a] 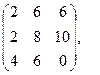
[a] 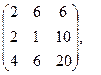
[a] 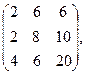
[a] 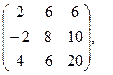
[a] 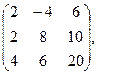
[q]3:1: Найти А-В , если 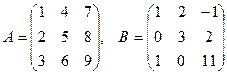
[a] 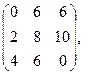
[a] 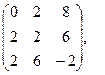
[a] 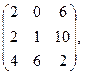
[a] 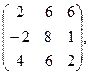
[a] 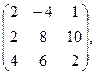
[q]3:1: Найти 2А+В, если 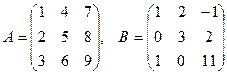
[a] 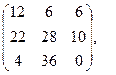
[a] 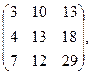
[a] 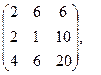
[a] 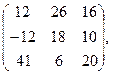
[a] 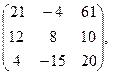
[q]3:1: Найти 2 А-В, если 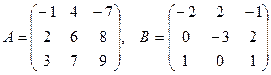
[a] 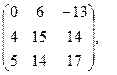
[a] 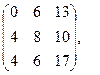
[a] 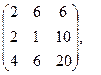
[a] 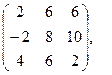
[a] 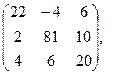
[q]3:1: Найти матрицу, обратную данной 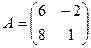
[a] 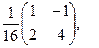
[a] 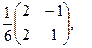
[a] 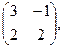
[a] 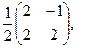
[a] 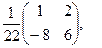
[q]3:1: Найти матрицу, обратную данной 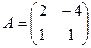
[a] 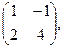
[a] 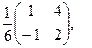
[a] 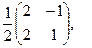
[a] 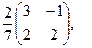
[a] 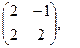
[q]3:1: Найти матрицу, обратную данной 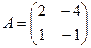
[a] 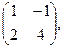
[a] 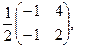
[a] 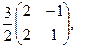
[a] 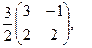
[a] 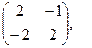
[q]3:1: Найти матрицу, обратную данной 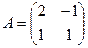
[a] 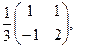
[a] 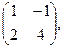
[a] 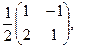
[a] 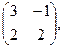
[a] 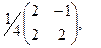
[q]3:1: Найти матрицу, обратную данной 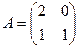
[a] 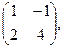
[a] 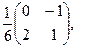
[a] 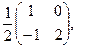
[a] 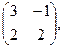
[a] 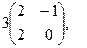 1
1
[q]3:1: Найти матрицу, обратную данной 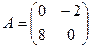
[a] 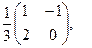
[a] 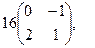
[a] 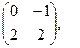
[a] 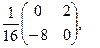
[a] 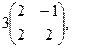
[q]3:1: Решить систему уравнений 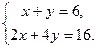
[a] 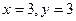
[a] 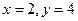
[a] 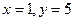
[a] 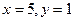
[a] 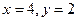
[q]3:1: Решить систему уравнений 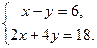
[a] 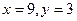
[a] 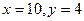
[a] 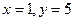
[a] 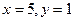
[a] 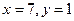
[q]3:1: Решить систему уравнений 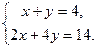
[a] 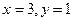
[a] 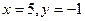
[a] 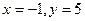
[a] 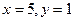
[a] 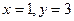
[q]3:1: Решить систему уравнений 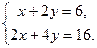
[a] 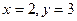
[a] 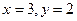
[a] 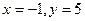
[a] 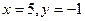
[a] нет решения 
[q]3:1: Решить систему уравнений 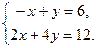
[a] 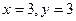
[a] 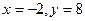
[a] 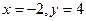
[a] 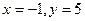
[a] 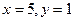
[q]3:1: Решить систему уравнений 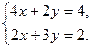
[a] 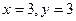
[a] 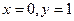
[a] 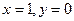
[a] 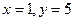
[a] 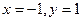
[q]3:1: Решить систему уравнений 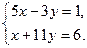
[a] нет решения
[a] 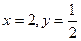
[a] 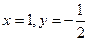
[a] 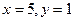
[a] 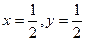
[q]3:1: Решить систему уравнений 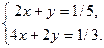
[a] 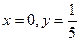
[a] 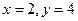
[a] нет решения
[a] 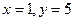
[a] 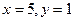
[q]3:1: Найти уравнение прямой, проходящей через точку А(2;3) параллельно оси ОХ
[a] у=6
[a] х+у=7
[a] х=3
[a] у=2
[a] у=3
[q]3:1: Найти уравнение прямой, проходящей через точку А(2;3) параллельно оси ОУ
[a] х=2
[a] х=3
[a] у=2
[a] у=3
[a] х+у=0
[q]3:1: Найти уравнение прямой, проходящей через точки А(2;3) и В(5;4)
[a] х=6
[a] х+у-7=9
[a] 2х-3у -7=0
[a] х-3у+7=0
[a] у-5=0
[q]3:1: Найти уравнение прямой, проходящей через точки А(3;1) и В(3;5)
[a] х+у=2
[a] у= 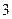
[a] х=-3
[a] х=3
[a] у- 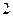 =0
=0
[q]3:1: Найти уравнение прямой, проходящей через точки А(3;1) и В(-4;1)
[a] х-у=2
[a] х=1
[a] у-2=0
[a] х+2у=3
[a] у=1
[q]3:1: Уравнение прямой проходящей через точки М1(х1,у1) и М2(х2,у2):
[a] 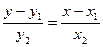
[a] 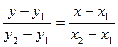
[a] 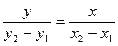
[a] 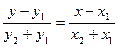
[a] 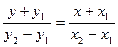
[q]3:1: Угол между двумя прямыми 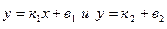
[a] 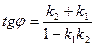
[a] 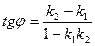
[a] 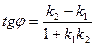
[a] 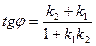
[a] 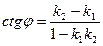
[q]3:1: Условие параллельности двух прямых 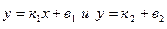
[a] 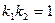
[a] 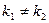
[a] 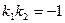
[a] 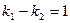
[a] 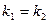
[q]3:1: Условие перпендикулярности двух прямых 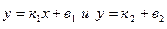
[a] 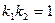
[a] 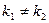
[a] 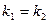
[a] 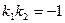
[a] 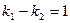
[q]3:1: Составить уравнение прямой, проходящей через точку А(2;1) параллельно прямой 3х-2у+2=0
[a] 3х+2у-4=0
[a] 3х-2у+4=0
[a] -3х-2у+4=0
[a] 3х+2у+4=0
[a] 3х-2у-4=0
[q]3:1: Составить уравнение прямой, проходящей через точку А(2;1) перпендикулярно прямой 3х-2у+2=0
[a] 3х+2у-7=0
[a] 2х-2у+4=0
[a] -3х+2у+4=0
[a] 3х+2у+7=0
[a] 2х+3у-7=0
[q]3:1: Найти расстояние от точки А(2;1) до прямой 3х-4у+3=0
[a] 2
[a] 3
[a] 1
[a] 4
[a] 5
[q]3:1: Найти расстояние от точки А(2;-1) до прямой 3х-4у+5=0
[a] 3
[a] 2
[a] 1
[a] 4
[a] 0
[q]3:1: Найти расстояние от точки А(0;6) до прямой 3х+4у-24=0
[a] 2
[a] 0
[a] 3
[a] 4
[a] 1
[q]3:1: Найти расстояние от точки А(0;6) до прямой 3х+4у+6=0
[a] 6
[a] 2
[a] 3
[a] 4
[a] 1
[q]3:1: Расстояние между точками 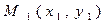 и
и 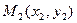
[a] 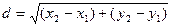
[a] 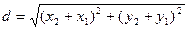
[a] 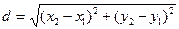
[a] 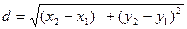
[a] 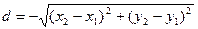
[q]3:1: Деление отрезка 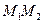 точкой
точкой 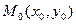 в данном отношении
в данном отношении 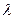 ,
,
если 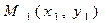 и
и 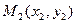
[a] 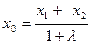 ;
; 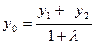

[a] - 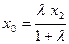 ;
; 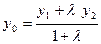
[a] 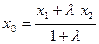 ;
; 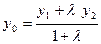
[a] - 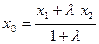 ;
; 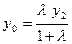
[a] 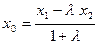 ;
; 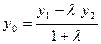
[q]3:1: Деление отрезка 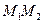 точкой
точкой 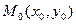 пополам,
пополам,
если 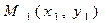 и
и 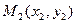
[a] 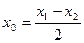 ;
; 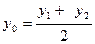

[a] - 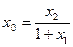 ;
; 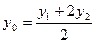
[a] 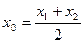 ;
; 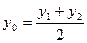
[a] - 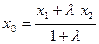 ;
; 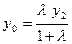
[a] 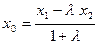 ;
; 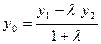
[q]3:1: Уравнение прямой, проходящей через точку 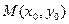 с угловым
с угловым
коэффициентом 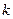
[a] 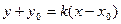
[a] 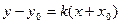
[a] 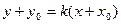
[a] 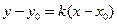
[a] 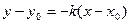
[q]3:1: Расстояние 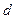 от точки
от точки 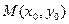 до прямой
до прямой 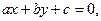
[a] 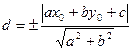
[a] 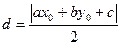
[a] 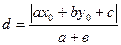
[a] 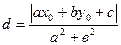
[a] 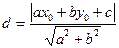
[q]3:1: Уравнение окружности с центром в точке 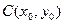 и радиуса
и радиуса 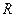
[a] 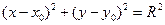
[a] 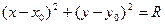
[a] 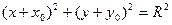
[a] 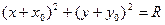
[a] 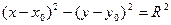
[q]3:1: Минором 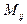 элемента
элемента 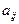 называется
называется
[a] определитель, полученный из определителя матрицы А вычеркиванием i-й строки и j-го столбца
[a] определитель, полученный из определителя матрицы А вычеркиванием j-й строки и j-го столбца
[a] определитель, полученный из определителя матрицы А вычеркиванием j-й строки
[a] определитель, полученный из определителя матрицы А вычеркиванием i-й строки и i-го столбца
[a] определитель, полученный из определителя матрицы А вычеркиванием i-й строки
[q]3:1: Длина вектора 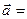
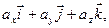
[a] 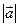 =
= 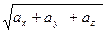
[a] 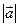 =
= 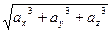
[a] 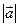 =
= 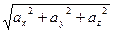
[a] 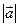 =
= 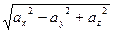
[a] 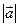 =
= 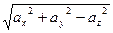
[q]3:1: Условие параллельности двух векторов 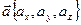 и
и 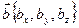
[a] 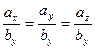
[a] 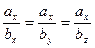
[a] 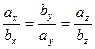
[a] 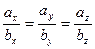
[a] 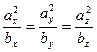
[q]3:1: Скалярное произведение векторов 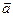 и
и 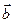 :
:
[a] 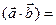
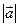
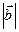
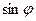
[a] 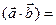
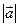
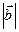
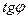
[a] 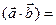
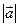
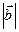
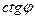
[a] 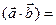
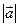 2
2 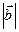 2
2 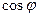
[a] 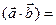
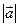
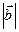
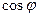
[q]3:1: Формула вычисления скалярного произведения векторов 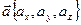 и
и 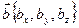
[a] 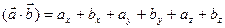
[a] 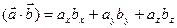
[a] 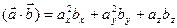
[a] 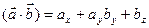
[a] 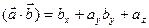
[q]3:1: Формула вычисления угла 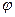 между векторами
между векторами 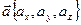 и
и 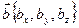
[a] 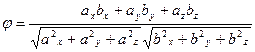
[a] 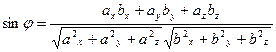
[a] 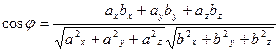
[a] 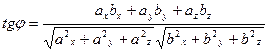
[a] 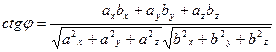
[q]3:1: Условие перпендикулярности двух векторов 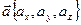 и
и 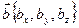
[a] 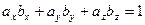
[a] 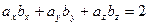
[a] 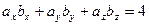
[a] 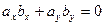
[a] 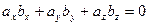
[q]3:1: Формула вычисления угла между двумя плоскостями
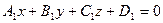 и
и 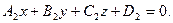
[a] 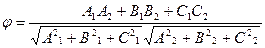
[a] 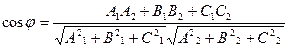
[a] 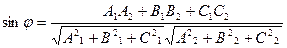
[a] 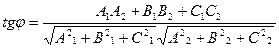
[a] 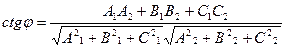
[q]3:1: Условие перпендикулярности двух плоскостей
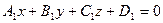 и
и 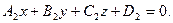
[a] 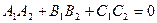
[a] 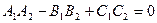
[a] 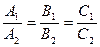
[a] 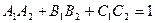
[a] 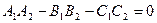
[q]3:1: Условие параллельности двух плоскостей
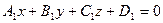 и
и 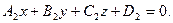
[a] 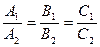
[a] 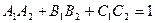
[a] 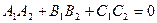
[a] 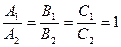
[a] 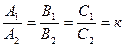
[q]3:1: Канонические уравнения прямой в пространстве, проходящей через т. М0(х0,у0) параллельно вектору 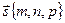
[a] 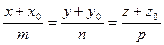
[a] 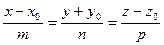
[a] 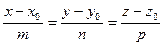
[a] 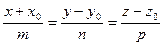
[a] 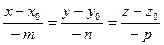
[q]3:1: Общие уравнения прямой в пространстве
[a] 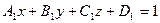 ,
, 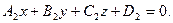
[a] 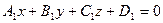 ,
, 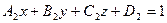
[a] 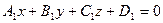 ,
, 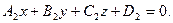
[a] 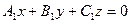 ,
, 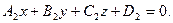
[a] 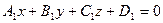 ,
, 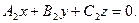
[q]3:1: Угол между прямой 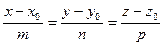 и плоскостью
и плоскостью 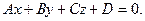
[a] 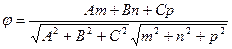
[a] 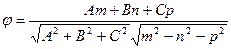
[a] 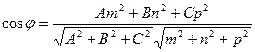
[a] 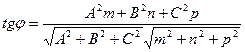
[a] 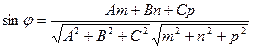
[q]3:1: Условия параллельности прямой 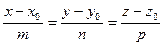 и плоскости
и плоскости 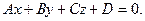
[a] 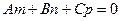
[a] 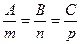
[a] 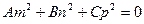
[a] 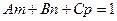
[a] 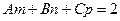
[q]3:1: Условия перпендикулярности прямой 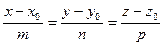 и плоскости
и плоскости 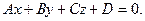
[a] 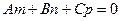
[a] 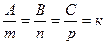
[a] 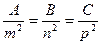
[a] 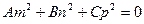
[a] 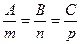
[q]3:1: Угол между двумя прямыми 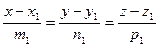 и
и 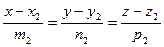
[a] 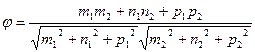
[a] 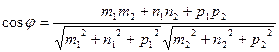
[a] 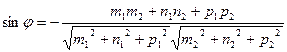
[a] 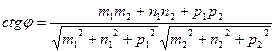
[a] 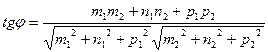
[q]3:1: Условия параллельности двух прямых 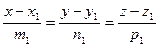 и
и 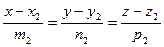 :
:
[a] 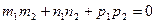
[a] 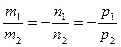
[a] 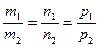
[a] 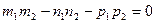
[a] 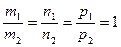
[q]3:1: Условия перпендикулярности двух прямых 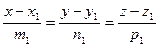 и
и 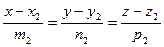 :
:
[a] 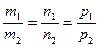
[a] 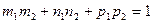
[a] 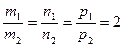
[a] 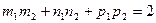
[a] 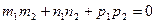
[q]3:1: Уравнение прямой 4х-3у+12=0 представить в виде уравнения с угловым коэффициентом
[a] у=4/3х+4
[a] у=3/4х+4
[a] у=4х-12
[a] х=3у -12
[a] х-у=1
[q]3:1: Уравнение прямой 4х-3у+12=0 представить в виде уравнения в отрезках на осях координат
[a] 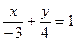
[a] 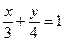
[a] 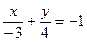
[a] 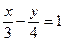
[a] 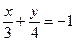
[q]3:1: Уравнение прямой 4х-3у+12=0 представить в виде нормального уравнения
[a] 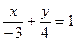
[a] 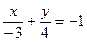
[a] 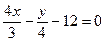
[a] 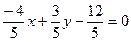
[a] 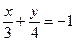
[q]3:1: Уравнение прямой 2х-3у+6=0 представить в виде уравнения с угловым коэффициентом
[a] у=3/4х+6
[a] у=4х-6
[a] х=3у -4
[a] х-у=12
[a] у=2/3х+2
[q]3:1: Уравнение прямой 2х-3у+6=0 представить в виде уравнения в отрезках на осях координат
[a] 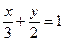
[a] 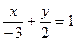
[a] 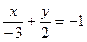
[a] 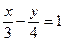
[a] 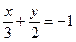
[q]3:1: Уравнение прямой 2х-3у+6=0 представить в виде нормального уравнения
[a] 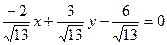
[a] 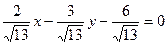
[a] 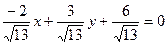
[a] 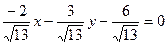
[a] 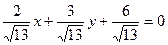
[q]3:1: Найти производную функции 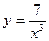
[a] 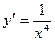
[a] 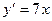
[a] 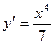
[a] 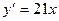
[a] 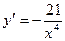
[q]3:1: Найти производную функции 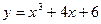
[a] 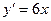
[a] 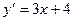
[a] 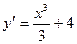
[a] 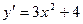
[a] 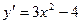
[q]3:1: Найти производную функции 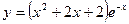
[a] 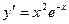
[a] 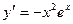
[a] 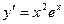
[a] 0
[a] 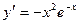
[q]3:1: Найти производную функции 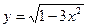
[a] 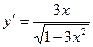
[a] 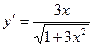
[a] 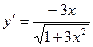
[a] 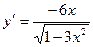
[a] 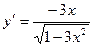
[q]3:1: Найти производную функции 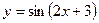
[a] 2cos (2x-3)
[a] -2cos (2x+3)
[a] cos (2x+3)
[a] -2xcos (2x+3)
[a] 2cos (2x+3)
[q]3:1: Найти производную функции 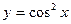
[a] 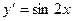
[a] 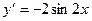
[a] 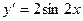
[a] 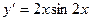
[a] 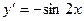
[q]3:1: Найти производную функции 
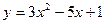
[a] -6х+5
[a] 6х-5
[a] -6х-5
[a] 6х+5
[a] 6х2
[q]3:1: Найти производную функции 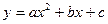
[a] 2ax-b
[a] 2ax+b
[a] -2ax+b
[a] -2ax-b
[a] 2ax+b+c
[q]3:1: Найти производную функции 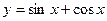
[a] 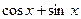
[a] - 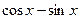
[a] 2 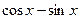
[a] 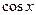
[a] 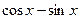
[q]3:1: Найти производную функции (1+2х)30
[a] -6(1+2х)29
[a] -60(1+2х)29
[a] 60(1-2х)29
[a] 60(1+2х)30
[a] 60(1+2х)29
[q]3:1: Найти производную функции (1-х2)10
[a] 20х(1-х2)9
[a] -20х(1+х2)9
[a] 20х(1+х2)9
[a] -20х(1-х2)10
[a] -20х(1-х2)9
[q]3:1: Найти производную функции 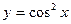
[a] 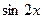
[a] 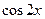
[a] - 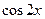
[a] 1
[a] 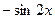
[q]3:1:Найти производную функции 
[a][+] 2
[a] 7
[a] 3
[a] 5
[a] 6
[q]3:1: Найти производную функции 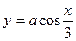
[a] 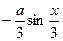
[a] 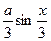
[a] 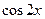
[a] - 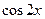
[a] 1
[q]3:1: Найти производную функции 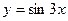
[a] -3cos3x
[a] 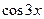
[a] 3cos3x
[a] - 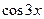
[a] 1
[q]3:1: Найти производную функции 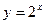
[a] - 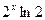
[a] 0
[a] 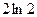
[a] 1
[q]3:1: Найти производную функции 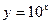
[a] 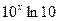
[a] 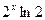
[a] - 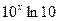
[a] 0
[a] 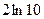
[a] 1
[q]3:1: Найти предел: 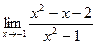
[a] 3
[a] 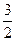
[a] 2
[a] 1
[a] 0
[q]3:1: Найти предел: 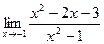
[a] 3
[a] 2
[a] 5
[a] 4
[a] 0
[q]3:1: Найти предел: 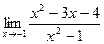
[a] 3
[a] 2
[a] 1
[a] 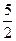
[a] 0
[q]3:1: Найти предел: 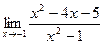
[a] 3
[a] 2
[a] 1
[a] 0
[a] 4
[q]3:1: Найти предел: 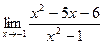
[a] 3,5
[a] 3
[a] 4
[a] 4,5
[a] 0
[q]3:1: Найти предел: 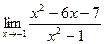
[a] 0
[a] 2
[a] 5
[a] 6
[a] 4
[q]3:1: Найти предел: 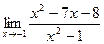
[a] 4,5
[a] 3,5
[a] 2
[a] 4
[a] 0
[q]3:1: Найти предел: 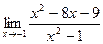
[a] 4
[a] 5
[a] 6
[a] 3
[a] 0
[q]3:1: Найти предел: 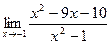
[a] 3,5
[a] 5
[a] 5,5
[a] 4,5
[a] 0
[q]3:1: Найти предел: 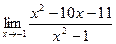
[a] 0
[a] 2
[a] 6
[a] 5
[a] 8
[q]3:1: Найти предел: 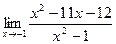
[a] 5,5
[a] 4
[a] 3
[a] 6,5
[a] 0
[q]3:1: Найти предел: 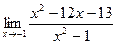
[a] 0
[a] 3
[a] 7
[a] 5
[a] 8
[q]3:1: Найти предел: 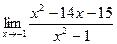
[a] 7
[a] 3
[a] 8
[a] 0
[a] 4
[q]3:1: Найти предел: 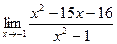
[a] 0
[a] 4,5
[a] 8,5
[a] 3,5
[a] 4
[q]3:1: Найти предел: 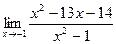
[a] 7,5
[a] 5,5
[a] 0
[a] 1
[a] 6,5
[q]3:1: Найти предел: 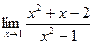
[a] 1,5
[a] 2,5
[a] 6,5
[a] 2
[a] 0
[q]3:1: Найти предел: 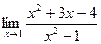
[a] 0
[a] 3,5
[a] 2,5
[a] 5,5
[a] 3
[q]3:1: Найти предел: 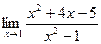
[a] 3,5
[a] 5,5
[a] 6
[a] 0
[a] 3
[q]3:1: Найти предел: 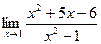
[a] [q]3:1: Найти производную функции 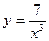
[a] 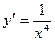
[a] 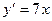
[a] 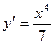
[a] 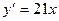
[a] 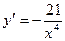
[q]3:1: Найти производную функции 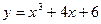
[a] 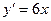
[a] 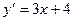
[a] 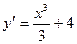
[a] 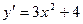
[a] 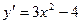
[q]3:1: Найти производную функции 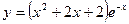
[a] 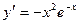
[a] 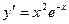
[a] 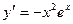
[a] 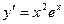
[a] 0
[q]3:1: Найти производную функции 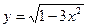
[a] 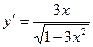
[[a] 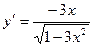
a] 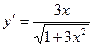
[a] 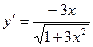
[a] 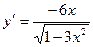
[q]3:1: Найти производную функции 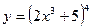
[a] 24х2(2х3-5)3
[a] -24х2(2х3+5)3
[a] 24х2(2х3+5)4
[a] 48х
[a] 24х2(2х3+5)3
[q]3:1: Найти производную функции 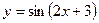
[a] 2cos (2x-3)
[a] -2cos (2x+3)
[a] cos (2x+3)
[a] -2xcos (2x+3)
[a] 2cos (2x+3)
[q]3:1: Найти производную функции 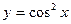
[a] 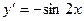
[a] 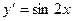
[a] 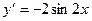
[a] 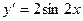
[a] 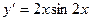
[q]3:1: Найти производную функции 
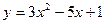
[a] -6х+5
[a] 6х-5
[a] -6х-5
[a] 6х+5
[a] 6х2
[q]3:1: Найти производную функции 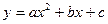
[a] 2ax-b
[a] -2ax+b
[a] 2ax+b
[a] -2ax-b
[a] 2ax+b+c
[q]3:1: Найти производную функции 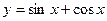
[a] 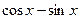
[a] 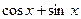
[a] - 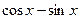
[a] 2 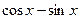
[a] 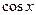
[q]3:1: Найти производную функции (1+2х)30
[a] 60(1+2х)29
[a] -6(1+2х)29
[a] -60(1+2х)29
[a] 60(1-2х)29
[a] 60(1+2х)30
[q]3:1: Найти производную функции (1-х2)10
[a] 20х(1-х2)9
[a] -20х(1-х2)9
[a] -20х(1+х2)9
[a] 20х(1+х2)9
[a] -20х(1-х2)10
[q]3:1: Найти производную функции 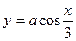
[a] 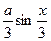
[a] 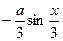
[a] 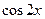
[a] - 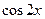
[a] 1
[q]3:1: Найти производную функции 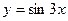
[a] -3cos3x
[a] 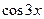
[a] 3cos3x
[a] - 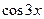
[a] 1
[q]3:1: Найти производную функции 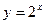
[a] - 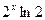
[a] 0
[a] 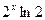
[a] 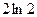
[a] 1
[q]3:1: Найти производную функции 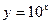
[a] 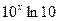
[a] - 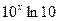
[a] 0
[a] 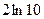
[a] 1
[q]3:1: Найти предел: 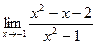
[a] 3
[a] 2
[a] 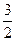
[a] 1
[a] 0
[q]3:1: Найти предел: 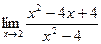
[a] 1
[a] 2
[a] 0
[a] 5
[a] 6
[q]3:1: Найти предел: 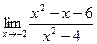
[a] 0
[a] 3
[a] 8
[a] 9
[a] 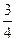
[q]3:1: Найти предел: 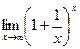
[a] 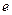
[a] 1
[a] 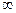
[a] 0
[a] -1
[q]3:1: Найти предел: 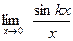
[a] 0
[a] 1
[a] 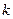
[a] 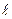
[a] -1
[q]3:1: Найти предел: 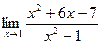
[a] 0
[a] 4,5
[a] 4
[a] 5,5
[a] 6
[q]3:1: Найти предел: 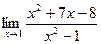
[a] 0
[a] 5,5
[a] 4,5
[a] 6,5
[a] 1
[q]3:1: Найти предел: 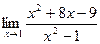
[a]5
[a] 0
[a] 1,5
[a] 5,5
[a] 6
[q]3:1: Найти предел: 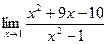
[a] 5,5
[a] 2,5
[a] 0
[a] 6
[a] 5
[q]3:1: Найти предел: 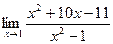
[a] 6
[a] 5
[a] 4
[a] 3
[a] 0
[q]3:1: Найти предел: 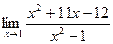
[a] 0
[a] 6,5
[a] 1
[a] 5
[a] 9
[q]3:1: Найти предел: 
[a] 5
[a] 3
[a]7
[a] 1
[a] 0
[q]3:1: Найти предел: 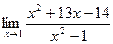
[a] 1
[a] 0
[a] 5
[a]7,5
[a] 3,5
[q]3:1: Найти предел: 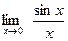
[a] 1
[a] 0
[a] 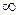
[a] -1
[a] - 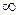
[q]3:1: Найти предел: 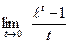
[a] 1
[a] 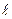
[a] 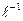
[a] 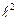
[a] 0
[q]3:1: Вычислить производную функции: 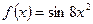
[a] 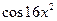
[a] 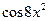
[a] 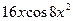
[a] 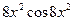
[a] 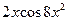
[q]3:1: Для всех 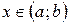 , график функции
, график функции 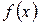 является выпуклым , если:
является выпуклым , если:
[a] 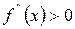
[a] 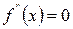
[a] 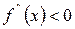
[a] 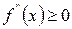
[a] 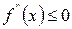
[q]3:1: Для всех 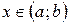 , график функции
, график функции 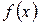 является вогнутым, если:
является вогнутым, если:
[a] 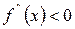
[a] 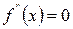
[a] 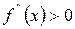
[a] 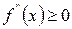
[a] 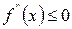
[q]3:1: Точка 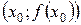 графика функции, отделяющая его выпуклую часть от вогнутой, называется
графика функции, отделяющая его выпуклую часть от вогнутой, называется
[a] точкой перегиба
[a] критической точкой
[a] точкой экстремума
[a] точкой минимума
[a] точкой максимума
[q]3:1: Точки, в которых 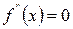 или
или 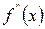 не существует называются:
не существует называются:
[a] точки экстремума
[a] точки минимума
[a] критическими точками ІІ рода
[a] точки максимума
[a] точки перегиба
[q]3:1: Прямая 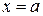 является вертикальной асимптотой кривой
является вертикальной асимптотой кривой 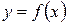 , если…
, если…
[a] 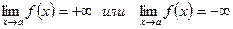
[a] 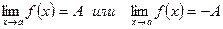
[a] 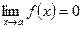
[a] 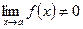
[a] 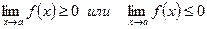
[q]3:1: Прямая 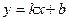 является наклонной асимптотой кривой
является наклонной асимптотой кривой 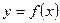 , если…
, если…
[a] 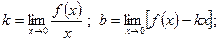
[a] 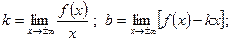
[a] 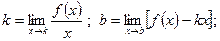
[a] 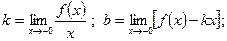
[a] 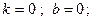
[q]3:1: Точка 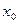 , в которой
, в которой 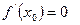 или
или 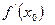 - не существует, называется ….
- не существует, называется ….
[a]критической точкой 1 рода
[a] стационарной точкой
[a] точкой минимума
[a] точкой максимума
[a] точкой экстремума
[q]3:1: Чему равна производная сложной функции, если 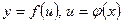
[a] 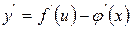
[a] 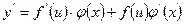
[a] 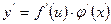
[a] 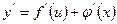
[a] 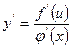
[q]3:1: Найти производную 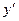 функции
функции 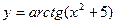 :
:
[a] 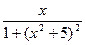
[a] 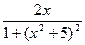
[a] 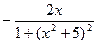
[a] 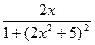
[a] 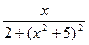
[q]3:1: Функция 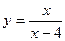 , при х = 4 имеет разрыв
, при х = 4 имеет разрыв
[a] Второго рода
[a] Первого рода
[a] третьего рода
[a] четвертого рода
[a] Не имеет разрыва
[q]3:1: y=ln x. Найти 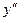 -?
-?
[a] 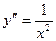
[a] 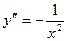
[a] 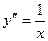
[a] 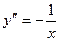
[a] 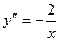
[q]3:1: Найти 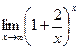
[a] 1
[a] 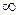
[a] 0
[a] 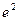
[a] -1
[q]3:1: Найти 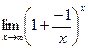
[a] 1
[a] 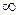
[a] 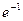
[a] 0
[a] -1
[q]3:1: Найти 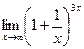
[a] 1
[a] 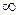
[a] 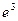
[a] -1
[a] 3
[q]3:1: Вычислить: 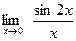
[a] 0
[a] 1
[a] 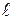
[a] -1
[a] 2
[q]3:1: Вычислить: 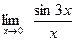
[a]3
[a] 0
[a] 1
[a] 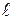
[a] -1
[q]3:1: Вычислить: 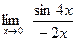
[a] -2
[a] 0
[a] 1
[a] 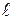
[a] -1
[q]3:1: Вычислить: 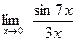
[a] 0
[a] 1
[a] 7/3
[a] 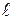
[a] -1
[q]3:1: Найдите производную функции. 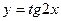
[a] 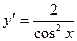
[a] 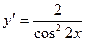
[a] 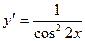
[a] 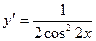
[a] 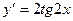
[q]3:1: Найдите производную функции. 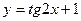
[a] 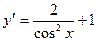
[a] 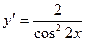
[a] 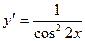
[a] 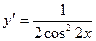
[a] 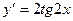
[q]3:1: Найдите производную функции. 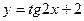
[a] 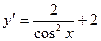
[a] 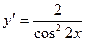
[a] 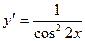
[a] 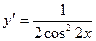
[a] 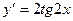
[q]3:1: Найдите производную функции. 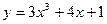
[a] 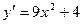
[a] 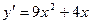
[a] 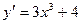
[a] 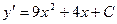
[a] 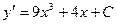
[q]3:1: Найдите производную функции. 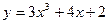
[a] 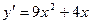
[a] 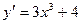
[a] 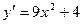
[a] 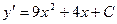
[a] 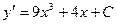
[q]3:1: Найти 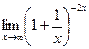
[a] 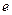
[a] 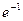
[a] 0
[a] 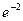
[a] -1
[q]3:1: Найти 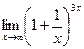
[a] 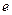
[a] 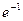
[a] 0
[a] 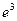
[a] -1
[q]3:1: Найти 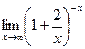
[a] 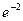
[a] 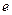
[a] 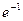
[a] 0
[a] -1
[q]3:1: Найти 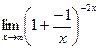
[a] 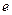
[a] 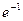
[a] 0
[a] 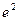
[a] -1
[q]3:1: Найти 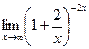
[a] 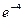
[a] 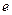
[a] 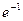
[a] 0
[a] -1
[q]3:1: Найти 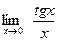
[a] 0
[a] 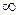
[a] 1
[a] –1
[a] - 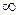
[q]3:1: Найти 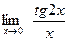
[a] 0
[a] 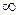
[a] 2
[a] –1
E) [a] - 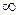
[q]3:1: Найдите предел: 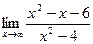
[a] 1
[a] 0
[a] 3
[a] 8
[a] 9
[q]3:1: Найдите предел: 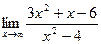
[a] 3
[a] 0
[a] 4
[a] 8
[a] 9
[q]3:1: Найдите предел: 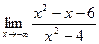
[a] 0
[a] 3
[a]1
[a] ) -1
[a] 9
[q]3:1: Найдите предел: 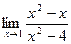
[a] -1
[a] 3
[a] 8
[a] 9
[a] 0
[q]3:1: Найдите предел: 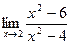
[a] 0
[a] 3
[a] 8
[a] 9
[a] 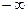
[q]3:1: Найти 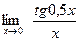
[a] 0
[a] 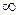
[a]0,5
[a] –1
[a] - 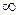
[q]3:1: Найти 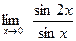
[a] 0
[a] 1
[a] 2
[a] –1
[a] - 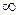
[q]3:1: Найти 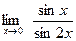
[a] 1
[a] 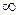
[a]1/2
[a] –1
[a] - 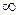
[q]3:1: Функция 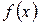 называется четной, если для любого x выполняется равенство
называется четной, если для любого x выполняется равенство
[a] 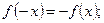
[a] 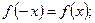
[a] 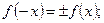
[a] 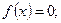
[a] 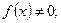
[q]3:1: Функция 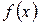 называется нечетной, если для любого x выполняется равенство
называется нечетной, если для любого x выполняется равенство
[a] 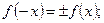
[a] 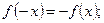
[a] 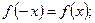
[a] 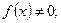
[a] 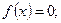
[q]3:1: Функция 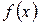 называется возрастающей, если для любых
называется возрастающей, если для любых 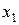 и
и 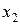 , таких что
, таких что 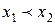 выполняется неравенство
выполняется неравенство
[a] 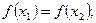
[a] 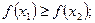
[a] 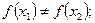
[a] 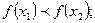
[a] 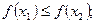
[q]3:1: Функция 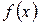 называется убывающей, если для любых
называется убывающей, если для любых 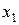 и
и 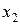 , таких что
, таких что 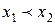 выполняется неравенство
выполняется неравенство
[a] 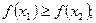
[a] 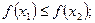
[a] 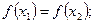
[a] 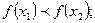
[a] 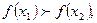
[q]3:1: Функция 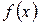 называется строго возрастающей, если для любых
называется строго возрастающей, если для любых 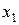 и
и 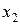 , таких что
, таких что 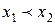 выполняется неравенство
выполняется неравенство
[a] 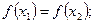
[a] 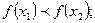
[a] 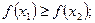
[a] 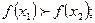
[a] 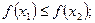
[q]3:1: Функция 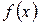 называется строго убывающей, если для любых
называется строго убывающей, если для любых 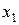 и
и 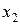 , таких что
, таких что 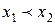 выполняется неравенство
выполняется неравенство
[a] 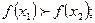
[a] 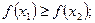
[a] 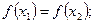
[a] 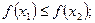
[a] 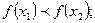
[q]3:1: Последовательность называется бесконечно малой, если ее предел равен:
[a] 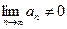
[a] 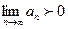
[a] 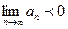
[a] Предел не существует.
[a] 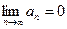
[q]3:1: Последовательность 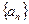 называется бесконечно большой, если:
называется бесконечно большой, если:
[a] 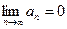
[a] 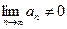
[a] 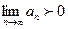
[a] 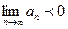
[a] 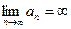
[q]3:1: Теорема Ролля: Если функция 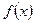 непрерывна на отрезке
непрерывна на отрезке 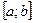 , дифференцируема на интервале
, дифференцируема на интервале 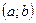 и
и 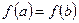 то найдется точка
то найдется точка 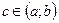 , такая, что выполняется:
, такая, что выполняется:
[a] 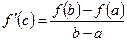
[a] 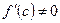
[a] 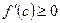
[a] 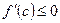
[a] 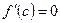
[q]3:1: Теорема Лагранжа: Если функция 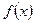 непрерывна на отрезке
непрерывна на отрезке 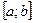 , дифференцируема на интервале
, дифференцируема на интервале 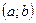 , то найдется точка
, то найдется точка 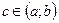 , такая, что
, такая, что
[a] 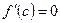
[a] 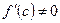
[a] 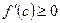
[a] 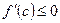
[a] 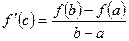
[q]3:1: Если функция 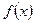 имеет положительную производную в каждой точке интервала
имеет положительную производную в каждой точке интервала 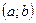 , то эта функция на этом интервале:
, то эта функция на этом интервале:
[a] не возрастает
[a] убывает
[a]возрастает
[a] строго убывает
[a] не меняется
[q]3:1: Если функция 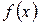 имеет отрицательную производную в каждой точке интервала
имеет отрицательную производную в каждой точке интервала 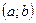 , то эта функция на этом интервале:
, то эта функция на этом интервале:
[a]убывает
[a] строго возрастает
[a] не убывает
[a] возрастает
[a] не меняется
[q]3:1: Точка 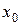 из области определения функции
из области определения функции 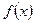 называется точкой минимума этой функции, если существует такая
называется точкой минимума этой функции, если существует такая 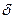 - окрестность точки
- окрестность точки 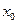 , что для всех
, что для всех 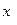 из этой
из этой 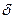 - окрестности выполняется неравенство...
- окрестности выполняется неравенство...
[a] 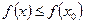
[a] 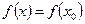
[a] 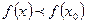
[a] 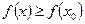
[a] 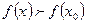
[q]3:1: Теорема Коши: Если функции 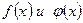 непрерывны на отрезке
непрерывны на отрезке 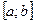 и дифференцируемы во всех его внутренних точках, причем
и дифференцируемы во всех его внутренних точках, причем 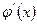 в этих точках не обращается в нуль, то в этом интервале существует хотя бы одно значение
в этих точках не обращается в нуль, то в этом интервале существует хотя бы одно значение 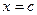 , для которого выполняется равенство:
, для которого выполняется равенство:
[a] 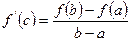
[a] 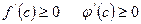
[a] 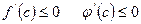
[a] 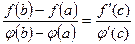
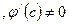
[a] 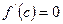
[q]3:1: Найти 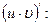
[a] 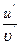
[a] 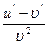
[a] 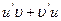
[a] 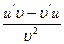
[a] 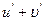
[q]3:1: Найти 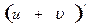
[a] 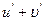
[a] 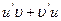
[a] 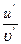
[a] 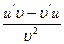
[a] 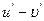
[q]3:1: Найти 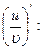
[a] 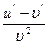
[a] 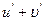
[a] 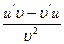
[a] 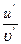
[a] 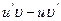
[q]3:1: Для раскрытия, каких неопределенностей можно пользоваться правилом Лопиталя ?
[a] 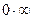
[a] ¥-¥ или 1¥
[a] 1¥ или ¥-¥
[a] 
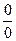 или
или 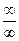
[a] 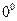 или ¥0
или ¥0
[q]3:1: Найдите следующий предел 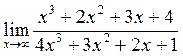
[a] 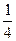 ;
;
[a] 4;
[a] 1;
[a] 0;
[a] ¥
[q]3:1: Найти 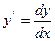 , если
, если 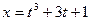 ;
; 
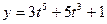
[a] 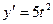
[a] 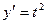
[a] 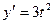
[a] 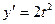
[a] 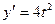
[q]3:1: Найти 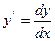 , если
, если 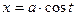 ;
; 
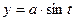
[a] tg t
[a] [a] -tg t
[a] ctg t
[a] –ctg t
[a] a
[q]3:1: Пусть в некоторой окрестности точки 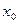 (кроме, быть может, самой точки
(кроме, быть может, самой точки 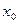 ) функции
) функции 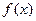 и
и 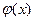 дифференцируемы и
дифференцируемы и 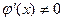 . Если
. Если 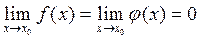 или
или 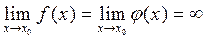 , то
, то 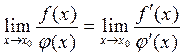 . Какая это теорема?
. Какая это теорема?
[a] теорема Лопиталя
[a] теорема Даламбера
[a] теорема Ферма
[a] теорема Ролля
[a] теорема Коши
[q]3:1: Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в интервале (a, b) и f(a) = f(b), то в интервале (a, b) найдется хотя бы одно значение 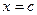 , при котором
, при котором 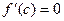 . Какая это теорема?
. Какая это теорема?
[a] теорема Лагранжа
[a] теорема Коши
[a] теорема Ферма
[a] теорема Лопиталя
[a] теорема Ролля
[q]3:1: Если функции 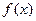 и
и 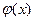 непрерывны на отрезке [a, b] и дифференцируемы в интервале (a, b), причем
непрерывны на отрезке [a, b] и дифференцируемы в интервале (a, b), причем 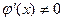 , то в этом интервале найдется хотя бы одно значение
, то в этом интервале найдется хотя бы одно значение 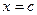 , при котором
, при котором 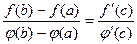 , где
, где 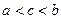 . Какая это теорема?
. Какая это теорема?
[a] теорема Лагранжа
[a] теорема Ролля
[a] теорема Лопиталя
[a] теорема Ферма
[a] теорема Коши
[q]3:1: Найти производную 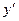 функции
функции 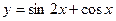 :
:
[a] 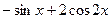
[a] 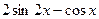
[a] 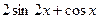
[a] 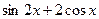
[a] 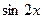
[q]3:1: Найти производную 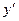 функции
функции 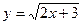 :
:
[a] 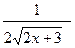
[a] 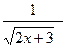
[a] 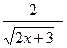
[a] 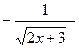
[a] 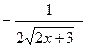
[q]3:1: Найти производную 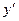 функции
функции 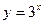 :
:
[a] 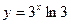
[a] 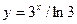
[a] 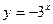
[a] 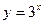
[a]