Структура, содержание и образовательные возможности учебно-методического комплекса
Ядром комплекса является структурированный в соответствии с целями и задачами курса лекционный материал (темы). В соответствующих разделах представлены вопросы для СРС и СРСП.
Кроме этого, учебно-методический комплекс предоставляет возможность самостоятельной проверки уровня освоения материала за счет ответов на предлагаемые вопросы и тестовые задания по теме лекции.
Особенностью данного учебно-методического комплекса является предоставляемая возможность более углубленного изучения материала путем подготовки рефератов или выполнения творческих заданий по темам, предлагаемым по курсу в целом.
Рекомендуемый порядок работы с учебно-методическим комплексом
Работу с учебно-методическим комплексом следует начинать со знакомства с его содержанием и программой курса. Это позволит обучающемуся сориентироваться в объеме предлагаемого к изучению материала, понять уровень его сложности и освоить навыки полномасштабного использования всех ресурсов, включенных в состав комплекса.
Знакомство с темой следует начать с прочтения всего текстового материала в полном объеме (первичное, ориентировочное чтение на общее понимание содержания и формирование завершенного образа темы).
После завершения изучения содержания темы следует, используя систему контрольных заданий и тестовых вопросов, определить степень знакомства с базовыми положениями лекции.
Безусловно, предлагаемый порядок работы с учебно-методическим комплексом может быть видоизменен и сокращен в зависимости от уровня подготовленности обучаемого и с учетом его индивидуально-психологических особенностей.
УТВЕРЖДЕНЫ
на заседании кафедры
«РЭТ»
учреждения «Университет «Туран»
Протокол № __ от «____»________ 2013 г.
Заведующая кафедрой,
доцент _____________ Вервейкина Л.С.
МАТЕРИАЛЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ОБУЧАЮЩЕГОСЯ
ПО ДИСЦИПЛИНЕ «Математика 1»
Самостоятельная работа студентов охватывает изучение учебников и учебных пособий по дмсциплине «Математика 1», ознакомление с монографическими исследованиями и научными публикациями в периодической печати на данную тему, анализ, решение практических задач по их применению, подготовку научных докладов, сообщений, рефератов, статей по отдельным аспектам и проблемам темы.
В ходе самостоятельной работы студентам необходимо научиться критически оценивать и анализировать теоретические и нормативные источники, уметь делать конкретные выводы, высказывать собственную точку зрения и предлагать собственные рекомендации по тем или иным вопросам. Все задания для самостоятельной работы выполняются в письменной форме.
Для выполнения заданий в рамках СРС студент должен изучить соответствующий лекционный материал, основную учебную и дополнительную литературу, нормативные правовые акты. Для облегчения поиска нормативно-правового материала целесообразно приобрести на электронном носителе (диск DVD) и использовать его постоянно в процессе работы.
При подготовке научного реферата, статьи, доклада, следует иметь в виду, что они являются формой самостоятельной работой, имеющей научный характер.
Для написания работы обязательным является использование как основной, так и дополнительной литературы, а также конспекта лекций и использование материала, пройденного на практических занятиях. Желательным является привлечение практического материала по теме исследования.
Обязательным условием письменных работ является наличие списка использованных источников. Сначала указываются нормативно-правовые акты в порядке убывания их юридической силы (Конституция, конституционный закон, закон, указ Президента и пр.), затем – специальная литература, расположенная в алфавитном порядке. Необходимо точно указывать автора и его инициалы, название работы, место, год издания, для статей – также название журнала (газеты), года, № (или даты издания), страниц, на которых напечатана статья; для нормативных правовых актов – их точное наименование, дату издания, ссылку на источник издания с указанием года, номера издания и номера статьи.
Например:
1) Т.К. Ерджанов Международное публичное право: Учебник. – Алматы: Жеті жарғы, 2006.
2) Шахаманов С. О практике государственной регистрации нормативных правовых актов //Правовая реформа в Казахстан. - 2001. - № 3. - С.49-52
3) Закон РК от 24 марта 1998 г. «О нормативных правовых актах» //Ведомости Парламента РК. - 1998. - № 3. Ст. 24
Не допускается механическое переписывание соответствующих положений из учебников, литературы и законодательства без их определенного осмысления и анализа. Оценка проведенной работы во многом будет зависеть от степени проявленной самостоятельности и творческого подхода студента. Обязательность, качество и своевременность выполнения заданий будут влиять на оценку рубежного контроля (промежуточного экзамена).
Темы для самостоятельной работы студентов.
Тема 1. Матрицы и определители. Системы линейных алгебраических уравнений.
Метод Гаусса. Правило Крамера. Решение матричных уравнений.
Тема 2. Линии второго порядка. Общее уравнение кривой второго порядка. Окружность, эллипс, гипербола, парабола.
Тема 3. Аналитическая геометрия в пространстве.
Прямая в пространстве. Канонические уравнения прямой. Векторное уравнение прямой. Уравнение прямой, проходящей через две точки. Плоскость. Общее уравнение плоскости в R3. Взаимное расположение прямой и плоскости, двух прямых, двух и трех плоскостей в пространстве R3. Приложения уравнения прямой и уравнения плоскости в пространстве.
Тема 4. Поверхности второго порядка.
Канонические формы уравнений поверхностей второго порядка. Исследование поверхностей второго порядка методом сечений.
Тема 5. Теоремы Ферма, Ролля, Лагранжа, их применение. Правило Лопиталя. Условия возрастания и убывания функции. Точки экстремума. Необходимые условия экстремума. Достаточные условия (признаки) существования экстремума.
Тема 6. Дифференцируемость функции. Дифференциал функции. Связь дифференциала с производной. Дифференциал суммы, произведения и частного.
Производные и дифференциалы высших порядков. Формула Лейбница.
Рекомендуемая литература.
1. Письменный Д.Т. Конспект лекций по высшей математике. М.2005
2. Шипачев В.С. Высшая математика. – М.: В Ш, 1985. –369 с. или любое другое более позднее издание: основы высшей математики, математический анализ и др.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т.1 – М.: Наука, 1985. – 432 с.
4. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа /Под ред. А.В. Ефимова и Б.П. Демидовича. – М.: Наука, 1986, 2002– 464 с.
5. Гусак А.А. Справочное пособие к решению задач: аналитическая геометрия и линейная алгебра. – Минск: ТетраСистемс, 1998. – 287 с.
6. Гусак А.А. Справочное пособие к решению задач: Математический анализ и дифференциальные уравнения. – Минск: ТетраСистемс, 1998.–287 с.
Преподаватель __________________
УТВЕРЖДЕНЫ
на заседании кафедры
«РЭТ»
учреждения «Университет «Туран»
Протокол № __ от «____»________ 2013 г.
Заведующая кафедрой,
доцент _____________ Вервейкина Л.С.
МАТЕРИАЛЫ ПО КОНТРОЛЮ И ОЦЕНКЕ УЧЕБНЫХ ДОСТИЖЕНИЙ ОБУЧАЮЩИХСЯ
[q]3:1: Вычислить расстояние между точками А(1;-2;-3) и В(3;1;-9)
[a] 3
[a] 5
[a] 6
[a] 2
[a] 7
[q]3:1: Вычислить расстояние между точками А(2;-3) и В(-1;1)
[a] 3
[a] 5
[a] 6
[a] 2
[a] 1
[q]3:1: Вычислить расстояние между точками А(-2;-3) и В(1;1)
[a] 3
[a] 60
[a] 5
[a] 2
[a] 1
[q]3:1: Вычислить расстояние между точками А(2;3) и В(-1;-1)
[a] 3
[a] 4
[a] 2
[a] 1
[a] 5
[q]3:1: Вычислить расстояние между точками А(-2;3) и В(1;-1)
[a] 3
[a] 0
[a] 5
[a] 2
[a] 1
[q]3:1: Вычислить расстояние между точками А(3;1;-9) и В(-1;1;-12)
[a] 3
[a] 6
[a] 5
[a] 2
[a] 1
[q]3:1: Вычислить расстояние между точками А(-3;1;-9) и В(1;1;-12)
[a] 5
[a] 4
[a] 6
[a] 2
[a] 11
[q]3:1: Вычислить расстояние между точками А(3;-1;9) и В(-1;-1;12)
[a] 3
[a] 5
[a] 0
[a] 2
[a] 1
[q]3:1: Вычислить расстояние от начала координат 0 до точки А(4;-2;-4)
[a] 3
[a] 5
[a] 2
[a] 6
[a] 1
[q]3:1: Вычислить расстояние от начала координат 0 до точки А(-4;3)
[a] 3
[a] 6
[a] 2
[a] 1
[a] 5
[q]3:1: Вычислить расстояние от начала координат 0 до точки А(-4;-3)
[a] 3
[a] 6
[a] 2
[a] 1
[a] 5
[q]3:1: Найти угловой коэффициент прямой 2х-у+3=0
[a] 3
[a] 6
[a] -1
[a] 1
[a] 2
[q]3:1: Найти угловой коэффициент прямой 2х+у+3=0
[a] 3
[a] -2
[a] 6
[a] -1
[a] 1
[q]3:1: Найти угловой коэффициент прямой 3х-у+3=0
[a] -3
[a] 3
[a] 6
[a] -1
[a] 1
[q]3:1: Найти угловой коэффициент прямой 8х-2у+3=0
[a] 3
[a] 4
[a] -4
[a] -1
[a] 1
[q]3:1: Найти угловой коэффициент прямой 4х-4у+3=0
[a] 3
[a] 6
[a] -1
[a] 1
[a] 12
[q]3:1: Найти угловой коэффициент прямой 9х-3у+8=0
[a] 5
[a] 0
[a] 3
[a] -1
[a] 1
[q]3:1: Найти угловой коэффициент прямой 14х-2у+3=0
[a] 3
[a] 7
[a] 6
[a] -1
[a] 1
[q]3:1: Найти угловой коэффициент прямой 10х+5у+3=0
[a] 3
[a] -2
[a] 6
[a] -1
[a] 1
[q]3:1: Найти уравнение прямой, проходящей через точки А(-1;3) и В(4;5)
[a] 2х-5у+17=0
[a] х= 3
[a] у+2у-6=0
[a] х-1=0
[a] у=1
[q]3:1: Найти уравнение прямой, проходящей через точки А(-1;2) и В(1;3)
[a] 2х-5у+17=0
[a] х-2у+5=0
[a] у+2у-6=0
[a] х-1=0
[a] х-у=1
[q]3:1: Найти уравнение прямой, проходящей через точки А(1;-2) и В(-1;3)
[a] 2х-5у+1=0
[a] у+2у-6=0
[a] 5х+2у-1=0
[a] х-1=0
[a] х-у=1
[q]3:1: Найти уравнение прямой, проходящей через точки А(-1;0) и В(-4;-5)
[a] х+у= 3
[a] у+2у-6=0
[a] 5х-3у+5=0
[a] х-2у+1=0
[a] у=1
[q]3:1: Найти уравнение прямой, проходящей через точки А(-2;2) и В(-1;3)
[a] х+у= 3
[a] у+2у-6=0
[a] х-1=0
[a] х-у+4=0
[a] у=1
[q]3:1: Найти уравнение прямой, проходящей через точки А(-1;-2) и В(1;-1)
[a] х-2у+2= 0
[a] у+2у-6=0
[a] х-1=0
[a] х-2у-3=0
[a] у=1
[q]3:1: Составить уравнение плоскости, которая проходит через точку М(2;1;-1) и имеет нормальный вектор 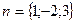
[a] х-2у-3z+3=0
[a] х-2у+3z+2=0
[a] х-2у+3z+1=0
[a] х-2у+3z+3=0
[a] х+2у+3z+3=0
[q]3:1: Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор 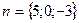
[a] 5х+3у=0
[a] 3х-5z=0
[a] 5х-3z=0
[a] 5х-3у-z=0
[a] 2x-3z=0
[q]3:1: Найти уравнение прямой, проходящей через точку А(-2;1) параллельно прямой 2х-у+1=0
[a] 5х+3у=0
[a] 3х-5у-1=0
[a] 5х-3у-3=0
[a] 2x-3у=0
[a] 2х-у+5=0
[q]3:1: Составить уравнение плоскости, проходящей через точку 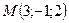 перпендикулярно вектору
перпендикулярно вектору 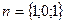
[a] 5х+3у-1=0
[a] 3х-5z=0
[a] х+z-5=0
[a] 5х-3у-z=0
[a] 2x-3z=0
[q]3:1: Написать уравнение плоскости проходящей через точку 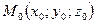 и имеющей нормальный вектор
и имеющей нормальный вектор 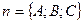 .
.
[a] 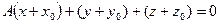
[a] 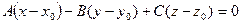
[a] - 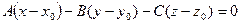
[a] 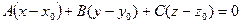
[a] 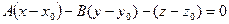
q]3:1: Составить уравнение плоскости, проходящей через точку 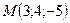 перпендикулярно вектору
перпендикулярно вектору 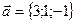
[a] 3х+у-z-18=0
[a] 5х+3у-1=0
[a] 3х-5z-2у+3=0
[a] 5х-3у-z=0
[a] 2x-3z=0
[q]3:1: Уравнение прямой с угловым коэффициентом представлено в виде:
[a] х+ку-1=0
[a] 3х--2у+3=0
[a] у=кх+в
[a] 5х-3у+в=0
[a] 2x-ку=в
[q]3:1: Установить, какие из следующих пар уравнений определяют параллельные плоскости:
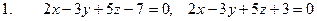 ;
;
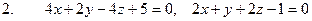 ;
;
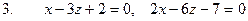
[a] 1 и 3
[a] 2 и 3
[a] 1,2 и 3
[a] 1 и 2
[a] нет таких плоскостей
[q]3:1: Установить, какие из следующих пар уравнений определяют перпендикулярные плоскости:
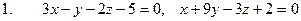 1.
1.
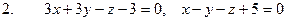 2.
2.
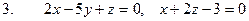 3.
3.
[a] 3
[a] 1 и 2
[a] 1
[a] 2 и 3
[a] нет перпендикулярных плоскостей
[q]3:1: Общее уравнение прямой представлено в виде:
[a] ах+ву+с=0
[a] ах--ву+с=0
[a] ах-ву+с=0
[a] 2x-ву=а
[a] ах-ву-с=0
[q]3:1: Определить, при каких значениях 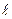 и m следующие пары уравнений будут определять параллельные плоскости:
и m следующие пары уравнений будут определять параллельные плоскости: 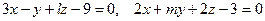
[a] 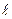 =2, m=1/2
=2, m=1/2
[a] 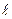 =-1, m= 1
=-1, m= 1
[a] 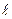 =3, m= -2/3
=3, m= -2/3
[a] 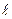 =1, m =2
=1, m =2
[a] 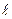 =-2, m=-1
=-2, m=-1
[q]3:1: Определить, при каких значениях 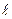 следующие пары уравнений будут определять перпендикулярные плоскости:
следующие пары уравнений будут определять перпендикулярные плоскости: 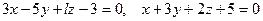
[a] 3
[a] 4
[a] 4,5
[a] 0
[a] 6
[q]3:1: Определить, при каких значениях 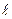 следующие пары уравнений будут определять перпендикулярные плоскости:
следующие пары уравнений будут определять перпендикулярные плоскости: 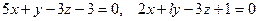
[a] -19
[a] 20
[a] -21
[a] 5
[a] 4
[q]3:1: Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 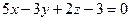
[a] 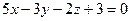
[a] 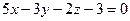
[a] 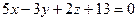
[a] 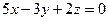
[a] 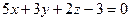
[q]3:1: Составить уравнение плоскости, которая проходит через точку 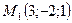 параллельно плоскости
параллельно плоскости 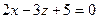
[a] 2х-3z-3=0
[a] 4x+3z-1=0
[a] x-y+2z=1
[a] x-3e+z-1=0
[a] 2y-z=0








