Этно равенство позволяет е болъшой точностью вычислмтъ приближенно приращение любой дифференцируемой функциию
Дифферевциал обычно находится значительно проще, чем прираюц ние функции, поэтому формула (24.3)широко применяется в вычислительной практике.
Прчмер 24. 3. Найти приближенное значение приращения функции y= 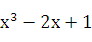 при x=2 и
при x=2 и 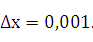 .
.
Решение: Применяем формулу (24.3) : 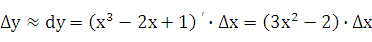
dy 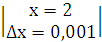 =
= 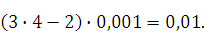
Итак, 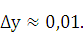
Посмотрим, какую погрешвость допустили, нычислив дяфференциал функции вместо ее приращения. Для этого найдем 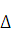 у:
у:
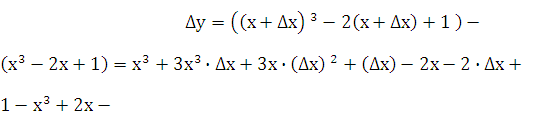 1=
1=
= 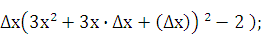
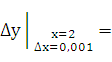 0,001
0,001 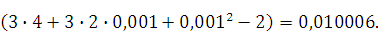
Абсолютная погрешность приближения равна
. 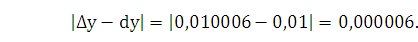
Подставляя в равенство (24.3) значения 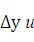 dy, получим
dy, получим
f 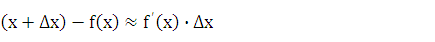 (24.4)
(24.4)
или
f 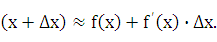
Формула (24.4) используется. для вычислений приближенных значений функцийю
Пример . Вычислить приближенно агсtg 1,05.
Решение: Рассмотрим функцию ‚f(х) = агсtg х. По формуле (24.4) имеем:
arctg 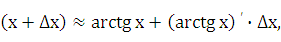
т. е.
arctg 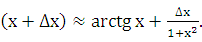
Так как x+ 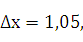 , то при х = 1 и
, то при х = 1 и 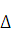 х = 0,05 получаем:
х = 0,05 получаем:
агсtg 1,05 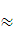 агсtg1 +
агсtg1 + 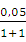 =
=  + 0,025
+ 0,025 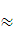 0,810.
0,810.
Можно показать, что абсолютная погрешность формулы (24.4) не пре-
вышает величины М 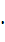 (
( 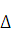 х)
х) 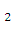 , где М — наибольшее значение ,
, где М — наибольшее значение , 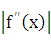 на сегменте
на сегменте 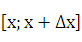 (см. с. 167)
(см. с. 167)
14-15 тема. Приложения производной
Теорема (достаточное условие возрастания функции)
Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.
Теорема (достаточное условие убывания функции), Если производная дифференцируемой функции отрицательна внутри некоторого промежутка 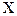 ,то она убывает на этом промежутке.
,то она убывает на этом промежутке.
Точка 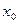 называется точкой максимума функции
называется точкой максимума функции 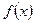 , если в некоторой окрестности точки
, если в некоторой окрестности точки 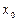 выполняется неравенство
выполняется неравенство 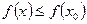 .
.
Точка 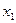 называется точкой минимума функции
называется точкой минимума функции 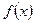 , если в некоторой окрестности точки
, если в некоторой окрестности точки 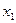 выполняется неравенство
выполняется неравенство 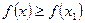 .
.
Значения функции в точках 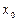 и
и 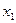 называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.
называются соответственно максимумом и минимумом функции. Максимум и минимум функции объединяются общим названием экстремума функции.
Для того, чтобы функция 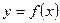 имела экстремум в точке
имела экстремум в точке 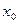 необходимо, чтобы ее производная в этой точке равнялась нулю
необходимо, чтобы ее производная в этой точке равнялась нулю 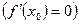 или не существовала.
или не существовала.
Первое достаточное условие экстремума.
Теорема. Если при переходе через точку 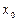 производная дифференцируемой функции
производная дифференцируемой функции 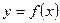 меняет свой знак с плюса на минус, то точка
меняет свой знак с плюса на минус, то точка 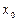 есть точка максимума функции
есть точка максимума функции 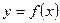 , а если с минуса на плюс, - то точка минимума.
, а если с минуса на плюс, - то точка минимума.
Схема исследования функции 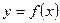 на экстремум.
на экстремум.
1.Найти производную 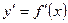 .
.
2.Найти критические точки функции, в которых производная 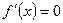 или не существует.
или не существует.
3.Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
4.Найти экстремумы ( экстремальные значения) функции.
Второе достаточное условие экстремума. Теорема.
Если первая производная 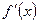 дважды дифференцируемой функции равна нулю в некоторой точке
дважды дифференцируемой функции равна нулю в некоторой точке 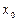 , а вторая производная в этой точке
, а вторая производная в этой точке 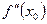 положительна, то
положительна, то 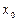 есть точка минимума функции
есть точка минимума функции 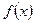 , если
, если 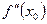 отрицательна, то
отрицательна, то 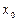 - точка максимума.
- точка максимума.
Для отыскания наибольшего и наименьшего значений на отрезке пользуемся следующей схемой.
1.Найти производную 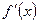 .
.
2.Найти критические точки функции, в которых 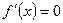 или не существует.
или не существует.
3.Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее 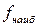 и наименьшее
и наименьшее 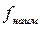 .
.
Функция 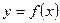 называется выпуклой вверх на промежутке Х, если отрезок соединяющий любые две точки графика лежит под графиком функции.
называется выпуклой вверх на промежутке Х, если отрезок соединяющий любые две точки графика лежит под графиком функции.
Функция 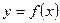 называется выпуклой вниз на промежутке Х, если отрезок соединяющий любые две точки графика лежит над графиком функции.
называется выпуклой вниз на промежутке Х, если отрезок соединяющий любые две точки графика лежит над графиком функции.
Теорема. Функция выпукла вниз (вверх) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает).
Теорема. Если вторая производная дважды дифференцируемой функции положительна ( отрицательна) внутри некоторого промежутка Х, то функция выпукла вниз (вверх) на этом промежутке.
Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.
Теорема ( необходимое условие перегиба). Вторая производная 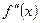 дважды дифференцируемой функции в точке перегиба
дважды дифференцируемой функции в точке перегиба 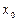 равна нулю, то есть
равна нулю, то есть 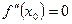 .
.
Теорема (достаточное условие перегиба). Если вторая производная 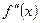 дважды дифференцируемой функции при переходе через некоторую точку
дважды дифференцируемой функции при переходе через некоторую точку 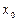 меняет свой знак, то
меняет свой знак, то 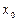 есть точка перегиба ее графика.
есть точка перегиба ее графика.
Схема исследования функции на выпуклость и точки перегиба:
1. Найти вторую производную функции 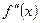 .
.
2. Найти точки, в которых второй производная 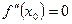 или не существует.
или не существует.
3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба .
4. Найти значения функции в точках перегиба.
При исследовании функции на построение их графиков рекомендуется использовать следующую схему:
1. Найти область определения функции.
2. Исследовать функцию на четность- нечетность.
3. Найти вертикальные асимптоты
4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Глоссарий
| № п/п | Новые понятия | Содержание |
| 1 | Достаточные условия возрастания (убывания ) функции | Если функция 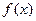 дифференцируема на (а,в) и дифференцируема на (а,в) и 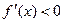 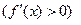 на этом интервале, то функция на этом интервале убывает ( возрастает). на этом интервале, то функция на этом интервале убывает ( возрастает).
|
| 2. | Экстремум функции | Точка 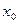 называется точкой максимума (минимума) функции называется точкой максимума (минимума) функции 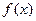 , если в некоторой ее окрестности выполняется неравенство , если в некоторой ее окрестности выполняется неравенство 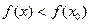 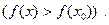
|
| 3. | Необходимое условие экстремума | Для того, чтобы функция 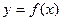 имела экстремум в точке имела экстремум в точке 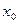 , необходимо, чтобы ее производная , необходимо, чтобы ее производная 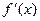 в этой точке равнялась нулю или не существовала: в этой точке равнялась нулю или не существовала: 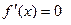 или не существует. или не существует.
|
| 4. | Достаточное условие экстремума | Если при переходе критической точки слева направо производная 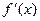 меняет свой знак с плюса на минус, то в данной точке функция имеет максимум, а если с минуса на плюс- минимум. меняет свой знак с плюса на минус, то в данной точке функция имеет максимум, а если с минуса на плюс- минимум.
|
| 5. | Выпуклость и вогнутость графика функции | Функция 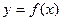 называется выпуклой (вогнутой) на интервале (а,в) , если все точки графика функции лежат ниже (выше) любой касательной к кривой называется выпуклой (вогнутой) на интервале (а,в) , если все точки графика функции лежат ниже (выше) любой касательной к кривой
|
| 6. | Достаточные условия выпуклости и вогнутости графика функции | Если вторая производная 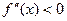 ( ( 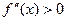 ) на интервале (а,в), то на этом интервале график функции выпуклый (вогнутый). ) на интервале (а,в), то на этом интервале график функции выпуклый (вогнутый).
|
| 7. | Точка перегиба | Точка на кривой, отделяющая выпуклую часть от вогнутой, называется точкой перегиба графика функции. |
| 8. | Необходимое условие перегиба | Вторая производная в точке перегиба равна нулю или не существует : 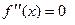 или не существует. или не существует.
|
| 9. | Достаточное условие перегиба | Если вторая производная 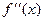 при переходе через критическую точку при переходе через критическую точку 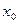 меняет свой знак, то в этой точке график функции имеет перегиб. меняет свой знак, то в этой точке график функции имеет перегиб.
|
| 10. | Асимптоты графика функции | Асимптотой графика функции 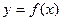 называется прямая, такая, что расстояние от точки называется прямая, такая, что расстояние от точки 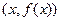 до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
|
| 11. | Вертикальные и наклонные асимптоты | Прямая 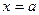 является вертикальной асимптотой для функции является вертикальной асимптотой для функции 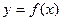 , если , если 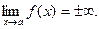 Прямая
Прямая 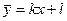 является наклонной асимптотой, если: является наклонной асимптотой, если:
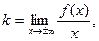 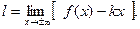
|
ПЛАН ПРАКТИЧЕСКИХ ЗАНЯТИЙ
| № п/п | Название темы семинара | Учебные часы | |
| 1 | 9. Матрицы и определители. 10. Определители 2-го, 3-го порядка, n-го порядка и их свойства. Матрицы, действия над матрицами и их свойства. Обратная матрица. | 1/0 | |
| 2 | Системы линейных алгебраических уравнений. Метод Гаусса. Правило Крамера. Решение матричных уравнений | 1/1 | |
| 3 | Векторная алгебра Линейные операции над векторами. Линейные пространства. Линейно-независимые системы векторов. Базис пространства, координаты вектора. Скалярное и векторное произведения векторов в R3. Смешанное произведение и его свойства | 1/1 | |
| 4 | Аналитическая геометрия на плоскости. Координатная ось и прямоугольная система координат. Полярные координаты. Прямая линия на плоскости, ее уравнения. Расстояние от точки до прямой. Угол двух прямых. | 2/1 | |
| 5 | Линии второго порядка. Общее уравнение кривой второго порядка. Окружность, эллипс, гипербола, парабола. | 1/0 | |
| 6 | Аналитическая геометрия в пространстве. Прямая в пространстве. Канонические уравнения прямой. Векторное уравнение прямой. Уравнение прямой, проходящей через две точки. Плоскость. Общее уравнение плоскости в R3. Взаимное расположение прямой и плоскости, двух прямых, двух и трех плоскостей в пространстве R3. Приложения уравнения прямой и уравнения плоскости в пространстве | 2/1 | |
| 7 | Поверхности второго порядка. Канонические формы уравнений поверхностей второго порядка. Исследование поверхностей второго порядка методом сечений | 1/0 | |
| 8 | Множество вещественных чисел. Числовые последовательности. Предел числовой последовательности. Существование предела монотонной ограниченной последовательности. Число е, натуральные логарифмы. 11. Функции и их свойства: Сложная функция, неявно заданная функция, параметрически заданнная функция. Четные и нечетные функции, периодическая функция, монотонные функции, обратная функция. Основные элементарные функции и их графики. Предел функции. Свойства функций, имеющих предел. | 1/0 | |
| 9 | Непрерывность функции. Непрерывность основных элементарных функций. Свойства непрерывных в точке функций. Односторонние пределы. Односторонняя непрерывность. Точки разрыва функции и их классификация. Свойства функций, непрерывных на отрезке. | 1/1 | |
| 10 | Дифференциальное исчисление функций одной переменной. Производная функции, ее геометрический и физический (механический) смыслы. Правила дифференцирования. Производная суммы, произведения и частного (обзор теорем школьного курса). Таблицы производных элементарных функций. | 1/1 | |
| 11 | Производная сложной функции. Производная обратной функции. Производные обратных тригонометрических функции. Функции, заданные параметрически, их дифференцирование. | 1/1 | |
| 12 | Дифференцируемость функции. Дифференциал функции. Связь дифференциала с производной. Дифференциал суммы, произведения и частного. Производные и дифференциалы высших порядков. Формула Лейбница. | 1/1 | |
| 13 | Исследование функций на выпуклость и вогнутость. Точки перегиба. Асимптоты кривых. Общая схема исследования функций и построение ее графика. | 1/1 |
Преподаватель кафедры: __________________
СОГЛАСОВАНО:
Заведующий кафедрой
«_________»________________________2012 г.
УТВЕРЖДЕНЫ
на заседании кафедры
«РЭТ»
учреждения «Университет «Туран»
Протокол № __ от «____»________ 2013 г.
Заведующая кафедрой,
доцент _____________ Вервейкина Л.С.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
«Математика 1»
(по работе с учебно-методическим комплексом)








