Понятие дифференциала функции
Пусть функция у=f(х) имеет в точке х отличную от нуля производную
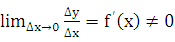 . Тогда, по теореме о связи функции, ее предела
. Тогда, по теореме о связи функции, ее предела
и бесконечно малой функции, можно записать 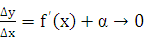
при 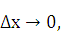 или
или 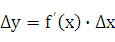 +
+ 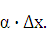 .
.
Таким образом, приращение функции 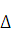 у представляет собой сумму
у представляет собой сумму
двух слагаемых ‚ 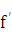 (х)
(х) 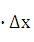 и
и 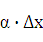 , являющихся бесконечно малыми при
, являющихся бесконечно малыми при 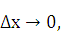
Поэтому первое слагаемое ‚ 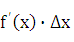 называют главной частью приращения функции
называют главной частью приращения функции 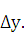
Дифференциалом функции –y= 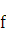 (х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df (х)):
(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy (или df (х)):
dy=  (24.1)
(24.1)
Дифференциал dy называют также дифференцалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у = х.
Так как 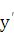 =
= 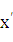 = 1, то, согласно формуле (24.1), имеем dy= dx =
= 1, то, согласно формуле (24.1), имеем dy= dx = 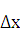 т. е. дифференциал независимой переменной равен приращению этой переменной: dx=
т. е. дифференциал независимой переменной равен приращению этой переменной: dx= 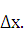
Поэтому формулу (24.1) можно записать так:
dy=  (24.2)
(24.2)
иными словами, дифференциал функции равен произведению производной этаой функции на дифференциал независимой переменной.
Из формулы (24.2) следует равенство 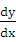 =
= 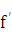 (х). Теперь обозначение
(х). Теперь обозначение
Производной 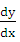 можно рассматривать как отношение дифференциалов dy и dx.
можно рассматривать как отношение дифференциалов dy и dx.
Пример 24.1. Найти дифференциал функции
f 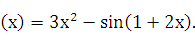 .
.
Решение: По формуле dy= 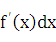 находим
находим
dy= 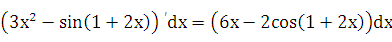 .
.
Пример 24.2. Найти диферинциал функции.
Y= 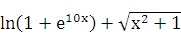 .
.
Вычислить dy при х = 0, dx=0,1..
Решение:
dy= 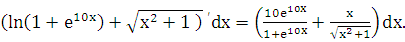
Подставив x=0 и dх = 0,1, получим
dy 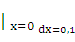 =
= 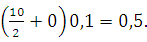
Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала,
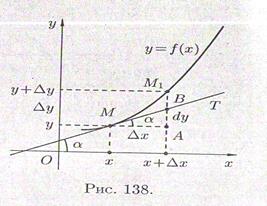 для этого проведем к графику функции у = f(х)
для этого проведем к графику функции у = f(х)
в точке М(х;у) касательную МТ и рассмотрим
ординату этой касательной для точки x+ 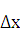
(см. рис. 138)
. На рисунке АМ = 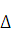 х, АM
х, АM 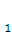 =
= 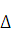 у. Из прямоугольного
у. Из прямоугольного
треугольника М АВ имеем: -
tg 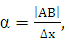 т. е.
т. е. 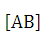 = tg
= tg 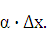 .
.
Но, согласно геометрическому смыслу
производной, tg 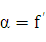 (х). Поэтому АВ =
(х). Поэтому АВ =
= 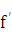 (х)
(х) 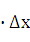 .
.
Сравнивая полученный результат с
формулой (24.1), получаем dу = АВ, т. е. дифференциал функции у =f(х) в тючке х равен приращению ординаты касательной к графику функции в этои точке, когда х получит приращение 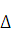 х.
х.
В этом и состоит геометрический смысл дифференциала.
Применение дифференциала к приближенным вычисления
Как уже известно, приращение 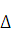 у функции у f(х) в точке х можно представить в виде
у функции у f(х) в точке х можно представить в виде 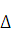 у =
у = 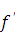 (х)
(х) 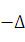 х +
х + 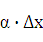 , где
, где 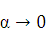 при
при 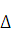 х
х 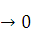 ,или
,или 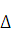 у = dy+
у = dy+ 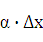 . Отбрасьювая бесконечно малую
. Отбрасьювая бесконечно малую 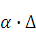 х более высокого порядка, чем
х более высокого порядка, чем 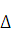 х,- получаем приближенное равенство
х,- получаем приближенное равенство
 y
y 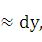
причем это равенство тем точнее, чем меньше 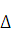 x
x








