Производные высших порядков
Производные высших порядков явно заданной функции
Производная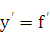 
(х) функции у = f(х) есть также функция от х и называется производной первого порядка.
Если функция ‚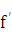 
(х) дифференцируема, то ее производная называется
производной второго порядка и обозначается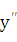 
(или 
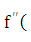х),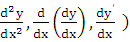 
Итак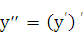 
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у” (или ‚“(х),
Итак,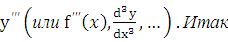 
, 
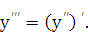
Производной n-го порядка (или n-й производной) называется производная от производной (n— 1) порядка:
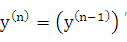
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (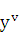 
или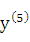 
— производная пятого порядка).
.
Механический смысл производной второго порядка
Пусть материальная точка М движется прямолинейно по закону
S= f(t). Как уже известно, производная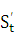 
равна скорости точки в дан-
ный момент времени: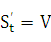 
.
Покажем, что вторая пронзводная от пути по времекп есть величина
ускореня прямолинейного движения точки, т. е.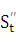 
= а.
Пусть в момент времени t скорость точки равна V, а в момент t+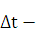 
-
скорость равна V+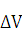 
, т. е. за промежуток времени 
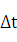. скорость измени-
лась на величину .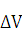
Отношение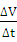 
выражает среднее ускорение движения точки за время 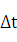. Предел этого отношения при 
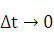называется ускорением точки М
в данный момент t и обозначается буквой а: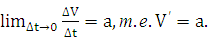 
.
Но V=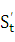 
. Поэтому а= ( ) 
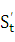, т. е. а = ‘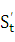
.Производные высших порядков от функций, заданных параметрически
Пусть функция у = f(х) задана параметрическими уравнениями
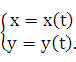
Как известно, первая производная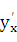 
у находится по формуле
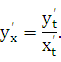
(23.1)
Найдем вторую производную от функции заданной параметрически.
Из определения второй производной и равенства (23.1) следует, что
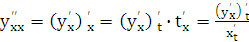, т.е.
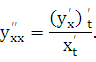
Аналогично получаем
,…
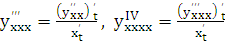Пример 23.3. Найти вторую производную функции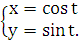 
Решение: По формуле (23.1)
.
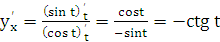Тогда по формуле (23.2)
.
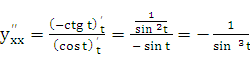Заметим, что найти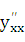 
можно по преобразованной формуле (23.2):
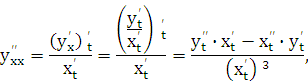
запоминать которую вряд ли стоит.
13 тема. ДИФФЕРЕНЦИАЛ ФУНКЦИИ