12 тема. Дифференцирование неявных и параметрически заданных функций
Неявно заданная функция
Если функция задана уравнением у =f (х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявнъм заданием функции понимают задание функции в виде
уравнения F(х; у) = 0, не разрешенного относительно у.
Всякую явно заданную функцию у=f(х) можно записать как неявно
заданную уравнением f(х) - у = 0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относи-
тельно у (например, у + 2х + соsy- 1 = 0 или 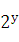 — х + у = 0).
— х + у = 0).
Если неявная функция задана уравнением F(х; у) = 0, то для нахо-
ждения производной от-у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение
по х, рассматривая прп этом у как функцию х, и полученное затем
уравнение разрешить относительно у’.
Производная неявной функции выражается через аргумент х и функ-
цию .
Пример 21.1. Найти производную функции у, заданную уравнением
x3 + у3 — 3ху=0.
Решение: Функция у задана неявно. Дифференцируем по х равенство
х3 + у3 — 3ху=0.
Из полученного соотношения
3х2+3у2у’—3(1 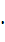 у+х
у+х 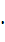 у
у  )=0
)=0
следует, что у2у  — ху
— ху  = у — х
= у — х 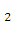 , т. е. у
, т. е. у  =
= 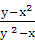
Функция, заданная параметрически
Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений
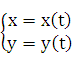
(21.1)
где — вспомогательная переменная, называемая параметром.
Найдем производную 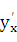 , считая, что функции (21.1) имеют производ-
, считая, что функции (21.1) имеют производ-
ные и что функция х = х( t). По правилу дифференцирования обратной функции
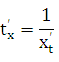
(21.2)
Функцию у = f(х), определяемую параметрическими уравнениями
(21.1), можно рассматривать как сложную функцию у = у(t), где t= 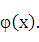
По правилу дифференцярования сложной функции имеем; 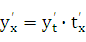
С учетом равенства (21.2) получаем

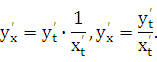
Полученная формула позволяет находить производную 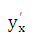 от функции
от функции
заданной параметрически, не находя непосредственной зависимости у от х.
Пример 21.2. Пусть 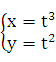 Найти
Найти 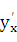 .
.
Решение: Имеем 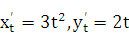 . Следовательно,
. Следовательно, 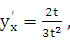 т. е.
т. е.
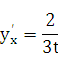
В этом можно убедиться, найдя непосредственно зависимость у от х.
Действительно, t= 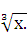 Тогда у=
Тогда у= 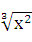 Отсюда
Отсюда 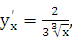 т. е. у=.
т. е. у=. 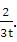
ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать. А затем результат продиффернцировать. Такую операцию называют логарифмическим дифференцированием.
Пример 22.1. Найти производную функции y= 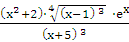
Решение: Можно найти 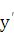 с помощью правил и формул дифференци- рования. Однако такой способ слишком громоздкий. Применим логарифмическое дифференцирование. Логарифмируем функцию:
с помощью правил и формул дифференци- рования. Однако такой способ слишком громоздкий. Применим логарифмическое дифференцирование. Логарифмируем функцию:
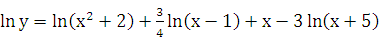 .
.
Дифференцируем это равенство по х:
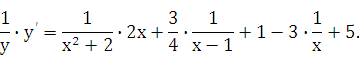
Выражаем 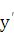 :
:
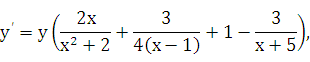
т. е. 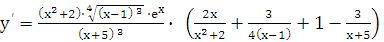
Существуют функции, производные которых находят лишь логарифмическим дифференцированием. К их числу относится так называемая степенно-показатаельная функция y= 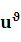 , где u= u(х) и
, где u= u(х) и 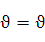 (х)
(х)
— заданные дифференцируемые функции от х. Найдем производную этой функции:
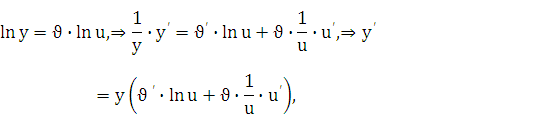
т. е.
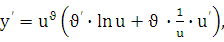
или .

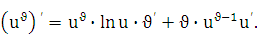
Сформулируем правило запоминания формулы (22.1):производная
степенно-показательной функции равна сумме производной показательной функции, при условии u= соnst, и производной степенной при условии 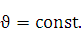 =
=
Пример 22.2. Найти производную функции у = 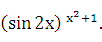 .
.
Решение: Пользуясь формулой (22.1), получаем:
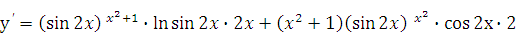 .
.
Отметим, что запоминать формулу (22.1) необязательно, легче запомнить суть логарифмического дифференцирования.








