6 тема : Аналитическая геометрия в пространстве

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Общее уравнение плоскости.

В пространстве существует единственная плоскость, проходящая через заданную точку М перпендикулярная к нормальному вектору n. Уравнение этой плоскости относительно данной системы координат имеет вид:

Ax+By+Cz+D=0 (1)

Уравнение (1) называется общим уравнением плоскости .

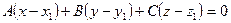(2)

а уравнение ( 2 )— уравнением плоскости, проходящей через точку М (х₁ , y ₁ , z ₁ ) перпендикулярно к вектору п = (А, В, С).

Расстояние от точки до плоскости. Пусть даны точка М₀ (x₀, y₀, z₀) и плоскость

Аx+By+Сz+D=О. (3)

Тогда расстояние от точки до плоскости находится по формуле

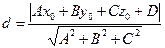(4)

Угол между двумя плоскостями находится как угол между векторами нормалями плоскостей по известной формуле

Условие параллельности и перпендикулярности двух плоскостей.

Условия паралельности имеют вид:

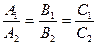(5)

Если плоскости взаимно перпендикулярны, то векторы n₁ и n₂ будут также взаимно перпендикулярны, и их скалярное произведение должно быть равно нулю:

А₁A₂ + В₁B₂ + С₁C₂ = О (7)

Прямая в пространстве.

Каноническое уравнение прямой, заданной точкой М₀(x₀,y₀,z₀) и направляющим вектором имеет виді:

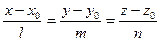(8)

а векторное уравнение: 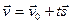(9)

параметрическое уравнение : 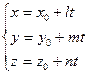(10)

Каноническое уравнение прямой проходящей через две точки

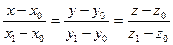(11)

а параметрическое урвнение: 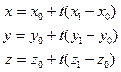(12)

Уравнение прямой заданной как пересечение двух плоскостей

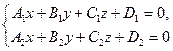(13)

Для того чтобы две прямые L₁ и L₂ в пространстве были ортогональнынеобходимо и достаточно, чтобы

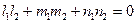, (14)

а для того чтобы они были паралельны необходимо выполнение условия 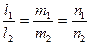(15)

7 тема: Поверхности второго порядка

Основные понятия. Поверхность и ее уравнение. Рассмотрим фигуру Ф и введем в пространстве аффинную систему координат О е₁е₂е₃ Условие, определяющим фигуру Ф в данной системе координат, называется уравнение или неравенство(или их система), которому удовлетворяют координаты точки, не принадлежащей фигуре Ф. Уравнение, определяющее фигуру Ф, называется уравнением фигуры Ф в данной системе координат.

При изучении геометрии в пространстве методом координат в качестве фигур чаще всего рассматривают поверхности. Примерами поверхностей являются плоскость, сфера, цилиндрические и конические поверхности и др. Условием, определяющим поверхность Ф в данной системе координат, являются как правило, уравнение, которое называется уравнением поверхности Ф.

Сфера и ее уравнение. Сферой называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не больше данного, от данной точки.

(x-a)² +(у-b)²+(z-c)²=r² уравнение сферы радиуса r с центром в точке С (а,b,с).

В частности, если центр сферы совпадает с началом координат, то а=b=с=0, поэтому уравнение (1) принимает вид

x²+y²+c²=r² (1)

Уравнение (1) можно записать в виде

x²+b²+c²+Ax+By+D=0 (2)

где

А=-2а, В=-2b С=-2с, D=a²+b²+c²+r² (З)

Эллипсоид и ее каноническое уравнение. Эллипсом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

x²/a²+y²/b²+z²/c²=1

это уравнение называется каноническим уравнением эллипсоида. Положительные числа а,Ь,с называются полуосями эллипсоида.

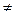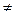Если а b, b с, c 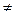a то эллипсоид называется трехосным. Так как в уравнение (1) x,y,z входят только в четных степенях, то эллипсоид, заданный уравнением (1)

симметричен относительно координатных плоскостей, начала координат и осей координат. Центр симметрии эллипсоида называется его центром, а оси симметрии эллипсоида — его осями. Каждая из осей пересекает эллипсоид в двух точках, которые называются его вершинами. У трехосного эллипсоида шесть вершин: А₁(a,0,0), А₂(-а,0,0), В₁(0,b,0), B₂(0,-b,0), C₁(0,0,c), С₂(0,0,-с).

Гиперболоиды и их канонические уравнения. Различают однополостные и двуполостные гиперболоиды.

Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе коордияат определяется уравнением

x²/a²+y²/b²+z²/c ²=1 (1)

это уравнение называется каноническим уравнением однополостного гиперболоида.

Так как в уравнение (1) x,y,z входят в четных степенях, то поверхность симметрична относительно плоскостей координат, осей координат (оси поверхности) и начала координат (центр поверхности). Две оси Ох и Оу пересекают поверхность в точках А₁ (а,О,0), А₂(-a,0,0) и В₁(0,b,0), В₂(0,-b,0). Эти оси называются действительными осями однополостного гиперболоида, а указанные точки их вершинами. Третья ось симметрии (ось Оz) не имеет общих точек с однополостным гиперболоидом и называется его мнимой осью. Положительные числа а,b,с называются полуосями однополостного гиперболоида.

Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

x²/a²+y²/b²+z²/ c²=-1 (2)

это уравнение называется каноническим уравнением двуполостного гиперболоида.

Из уравнения (2) следует, что поверхность симметрична относительно плоскостей координат, осей координат (оси поверхности) и начала координат (центр поверхности). Ось Оz пересекает в двух точках С₁(0,0,c) и С₂(0,0,-c) называемых вершинами двуполостного гиперболоида; сама эта прямая называется вещественной осью. Оси симметрии Ох и Оу не имеют с поверхностью (2) общих точек и называются мнимыми осями этой поверхности. Положительные числа а,b,с называются полуосями двуполостного гиперболоида.

x²/a²+y²/b²+z²/ c²=0

Это уравнение определяет коническую поверхность, которая называется асимптотическим конусом однополостного гиперболоида (1). Вершиной этого конуса служит центр поверхности (1).

Параболоиды и их канонические уравнения. Различают эллиптические и гиперболические параболоиды.

Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением

x²/a²-y²/b²=2z (3)

Это уравнение называется каноническим уравнением эллиптического параболоида.

Так как х и у входят в уравнение (1) в четных степенях, то эллиптический параболоид симметричен относительно плоскостей Охz, Оyz и относительно оси Оz (ось поверхности). Эта поверхность не симметрична относительно плоскости Оху, относительно осей Ох, Оу и начала координат.

Точка пересечения эллиптического параболоида с его осью называется вершиной. Если поверхность задана каноническим уравнением (1), то начало координат выбрано в вершине поверхности.

Если в уравнение (1) a=b, то получим уравнение поверхности в виде:

x²/a²+y²/a²=2z (2)

которая называется параболоидом вращения.

Поверхности вращения. Поверхность, которая вместе с каждой своей точкой содержит всю окружность, полученную вращением этой точки вокруг некоторой фиксированной прямой d , называется поверхностью вращения.