Эксцентриситет эллипса
Определение. Отношение фокусного расстояния к длине большой оси эллипса называется эксцентриситетом эллипса. Эксцентриситет
обозначим буквой е. По определению ,
ε = 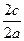 =
= 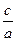
Гипербола и ее каноническое уравнение
Определение 11.3. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек, называемых фокусами гиперболы, есть величина постоянная (меньшая, чем расстояние между фокусами). Таким образом, если М — произвольная точка гиперболы, а Л и Е2 — ее фокусы, то по определению
/ F1M- F2M / = const
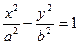
Свойство 1. Координатные оси являются осями симметрии, а начало координат — центром симметрии гиперболы.
Свойство 2. Гипербола пересекает ось абсцисс в точках Аi (—а, 0) и Аj,{а, 0) и не пересекает ось ординат.
Свойство 3. Координаты х и у любой точки гиперболы могут изменяться в пределах \х\ ≥ а, - ∞ < y <+ ∞.
Определение. Прямые, проходящие через начало координат и имеющие угловые коэффициенты Ь/а и — Ь/а, называются асимптотами гиперболы, заданной уравнением .
Определение Гипербола, полуоси которой равны между собой, называется равносторонней.
Определение Отношение фокусного расстояния гиперболы к ее действительной оси называется эксцентриситетом гиперболы
Как и в случае эллипса, эксцентриситет гиперболы обозначим буквой е. По определению для гиперболы
ε= 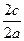 =
= 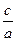
Парабола и ее каноническое уравнение
Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и данной прямой, называемой директрисой.
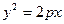
Свойство 1. Абсцисса любой точки параболы больше нуля.
Свойство 2. Парабола проходит через начало координат.
Свойство 3. Парабола симметрична относительно оси абсцисс.
Свойство 4. При неограниченном возрастании абсциссы х ордината у возрастает
Теорема Отношение расстояния от любой точки эллипса (гиперболы) до фокуса к расстоянию до соответствующей директрисы, есть величина постоянная, равная эксцентриситету эллипса (гиперболы).








