5 тема : кривые второго порядка

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Общее уравнение линии второго порядка.

Теперь рассмотрим уравнение второй степени с двумя переменными, т.е. уравнение.

а₁₁x² + 2а₁₂ xy+ а₂₂ y²+ 2а₁₃ x+ 2а₂₃ y+ а₃₃ =О

где хотя бы одно из чисел а₁₁ ,а₁₂ ,а₂₂ отлично от нуля, и предположить, что оно задано относительно декартовой прямоугольной системы координат О Все коэффициенты в левой части этого уравнения мы обозначили одной буквой а, снабженной двумя индексами, причем индексы 1 и 2 указывают, какая координата и сколько раз входит множителем в соответствующий член (например, а — коэффициент при квадрате второй координаты, 2а₁₂ — коэффициент при произведении первой и второй координат), а индекс З указывает, что коэффициент свободен от переменной. Некоторые коэффициенты взяты с множителем 2 для симметрии с последующими формулами. Кроме того, будем считать, что все коэффициенты симметричны относительно своих индексов, т.е. a _{i j} = a_{ji .}

Лиаметром линии второго порядка назыается прямая, являющаяся геометрическим местом середин паралельных хорд.

Линии второго порядка классифицируюся на центральные и нецентральные.

К центральным линиям относятся:

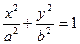-эллипс,

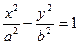-гипербола,

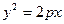-парабола.

К нецентральным относятся:

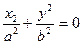-точка,

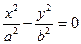-пара пересекающихся рпямых

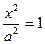-пара паралельных прямых

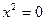- пара совпадающих прямых.

Координаты центра линии второго порядка определяются из уравнений: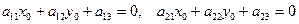

Уравнение касательной к линии в точке 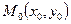имеет вид

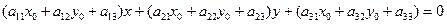
Уравнения линий второго порядка в полярных координатах

Используя свойство линий второго порядка, выведем уравнение линии второго порядка в полярной системе координат.

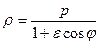
Окружность и ее уравнение

В прямоугольной системе координат окружность радиусом R с центром в точке С

(а, Ь) задается уравнением

( x - a)² +( y - b)² = R² (1)

где х, у — координаты произвольной точки М окружности.

Эллипс и его каноническое уравнение

Определение Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек (фокусов эллипса) есть величина постоянная (большая, чем расстояние между фокусами).

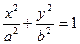
Постоянную величину, входящую в определение эллипса, обозначим через 2а (а>О), а расстояние между фокусами —2с

Свойство 1. Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии.

Свойство 2. Эллипс пересекает координатные оси в точках Аi(-а, 0),А2(а, 0), Ъ) и В2(0, —Ь).

Свойство 3. Координаты к и у любой точки эллипса удовлетворяют условиям: —а ≤х ≤а, −b ≤ y ≤ b.

Свойство 4. для точек эллипса, расположенных в первой координатной четверти, с возрастанием их абсциссы х от О до а ордината у убывает от b до О.

Оси координат называются осями симметрии, а начало координат — центром эллипса.