4 тема: Аналитическая геометрия на плоскости

Дата: 2025-05-25; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Различные уравнения прямой

Уравнение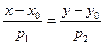

называется уравнением прямой,проходящей через данную точку в данном направлении (направление определяется углом а между прямой и осью Ох).

При выводе уравнения (1.1) мы исключили случай, когда прямая 1 перпендикулярна к оси Ох. Поэтому это уравнение задает только прямые, которые не перпендикулярны к оси Ох. Если же прямая / перпендикулярна к оси Ох, то, как легко установить, ее уравнение имеет вид х = а, где а — величина отрезка, отсекаемого этой прямой на оси Ох от начала координат.

Если, в частности, прямая 1 проходит через точку В, лежащую на оси Оу, и отсекает на этой оси отрезок величиной Ь, т. е.

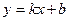
если прямая проходит через точку В ( О, Ь), то уравнение (1.1) принимает вид у — Ь = 1х или у = 1х — Ь. Это уравнение называется уравнением прямой с угловым коэффициентом. Числа 1 и Ь называются соответственно угловым коэффициентом прямой и начальной ординатой.

1.2 Уравнение прямой, проходящей через две точки

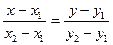
Уравнение прямой в отрезках

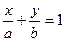
Как известно, две точки определяют единственную прямую, проходящую через эти точки. Поэтому, зная координаты двух произвольных точек прямой, можно составить ее уравнение.

1.3 Нормальное уравнение прямой

X cos 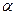+ y sin 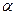- p = 0

2. Угол между двумя прямыми.

Определение: Если в прямоугольной системе координат на плоскости заданы две прямые 1 и 2 , то углом от прямой 1, до прямой 2 называется угол, на который надо повернуть прямую 2 вокруг какой-нибудь точки, леж щей на этой прямой, чтобы она стала параллельной или совпала бы с прямой 1,

Этот угол мы будем считать положительным, если поворот произведен против часовой стрелки, и отрицательным в противном случае. Из определения угла от одной прямой до другой следует, что определенный таким образом угол имеет бесконечное множество значений. Если В — одно из значений этого угла, то все значения его содержатся в выражении В + 1 где 1’ любое целое число. Значение

этого угла, удовлетворяющее условию О Во < УТ будем называть главным значением.

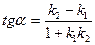
Условия параллельности и перпендикулярности двух прямых

A₁ x + B₁y + C₁ = 0;

A₂ x +B₂ y + C₂ = 0.

Угол между нормальными векторами п =(А_1,B₁) и n₂ = (А₂,B₂) прямых (2.1) равен одному из углов между этими прямыми .

Отсюда следует, что необходимое и достаточное условие взаимной перпендикулярности двух прямых имеет вид

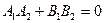
Если прямые заданы урвнениями с угловым коэффициентом, то условие перпендикулярности имеет вид 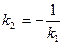.