Определение: Скалярным произведением ( ) векторов и называется число равное произведению длин векторов на косинус угла между ними
( 
) = 
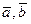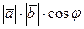(2)
Определим скалярное произведение векторов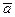 
и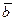 
через координаты этих векторов. Для векторов 
, 
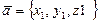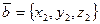, скалярное произведение равно: 
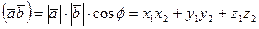(3).
Скалярное произведение двух векторов равно сумме произведений соответствующих координат. Если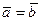 
болса, то 
, 
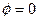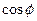=1 и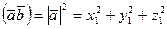 
, тогда длина вектора будет 
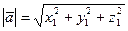(4).
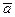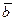Угол между векторами и определяется по формуле
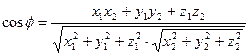(5).
Таким образом, скалярное произведение применяется при нахождении длин и величин углов.
в) Векторное произведение векторов и его свойства
В векторном пространстве V рассмотрим ортонормированный базис R=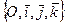 
. Пусть 
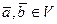не коллениарные векторы.
Определение. Векторным произведением векторов 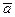и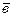 
называется вектор, обозначаемый 
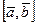и удовлетворяющий следующим условиям:
1) 
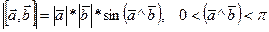
2) 
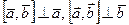
3)Тройки векторов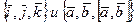 
одинаково ориентированы.
Если векторы 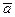и 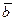коллинеарны, то их векторное произведение равно нулю. Пусть векторы заданы своими координатами и неколлинеарны:
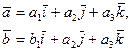
Тогда ранг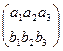 
=2, отсюда 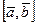векторное произведение не равно нулю. Координаты этого вектора относительно базиса 
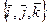удовлетворяют системе уравнений 
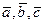, определитель которой отличен от нуля:
(3) 
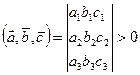
(2),(3)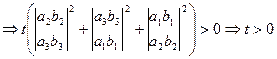 
.
Из первого условия определения найдем необходимое значение для t. Изветно, что
sin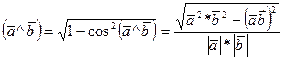 
(4) тогда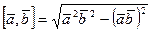 
.
Здесь
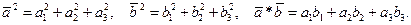
После вычислений находим:
(5) 
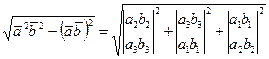
(6) 
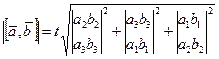
(4),(5),(6)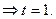 
(7)
(1), (2), (7)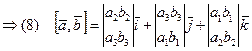 
Если векторы 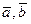коллинеарны, то ранг 
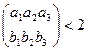и (8) формуле каждый определитель равен нулю. По определению 
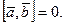ПОэтому и в этом случае (8) формула справедлива. Таким образом, доказана теорема.
ТЕОРЕМА. Если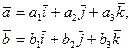 
то
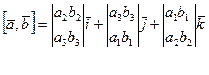
(8) формулу удобно записывать следующим образом:
(9) 
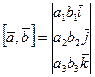
Свойства векторного произведения.
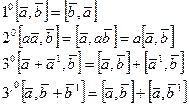
1), 2), 3) свойства следуют из (8) формулы.
Применение в ектор ного произведения .
1. Модуль векторного произведения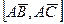 
равен площади параллелограмма ABCD
2. Площадь треугольника равна :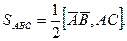 
Смешанное произведение векторов и его свойства .
Пусть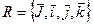 
положительно ориентированный ортонормированный базис.
Определение Смешанным произведением векторов 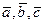называется число обозначаемое 
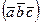и равное скалярному произведению вектора 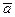на векторное произведение векторов 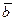и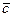 
.
Таким образом, 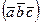- число.
1-ТЕОРЕМА (геометрический смысл смешанного проиведения).Если 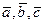- три некомпланарных вектора и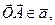 
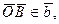
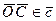, то абсолютное значение смешанного произведения 
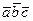равно объему параллелипипеда построенного на векторах 
:
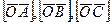(1) 
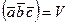
2- ТЕОРЕМА. Если в базисе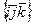 
координаты векторов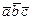 
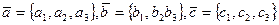, то
(2) 
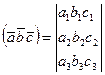
Свойства смешанного произведения:
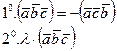
Применение смешанного произведения.
Пусть относительно прямоугольной системы координат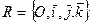 
тетраэдр ABCD задан своими вершинами:
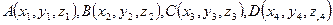. Тогда его объем находится по формуле:
.
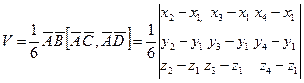