3 тема: Элементы векторной алгебры.
а) операции над векторами 
Обобщим понятия о векторах , известные со школьного курса геометрии
Вектором называется направленный отрезок АВ
Обозначается двумя заглавными или одной строчной буквой.
Длина(модуль) вектора АВ обозначается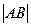 
.
Два вектора расположенные на одной прямой или на двух паралельных прямых называются колл и ниар н ы ми.
Три вектора расположенные в одной плоскости.
Суммой векторов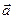 
и 
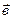называется вектор 
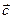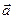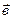= + , здесь вектор 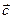соединяет начало вектора 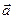с концом вектора 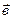(правило треугольника).
Кроме того, сумма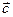 
векторов 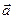и 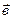определяется как диагональ параллелограма, построенного на этих векторах (правило параллелограмма).
Произведением вектора 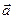на число k называется вектор 
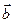=k* 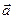, удовлетворяющий условиям: 1.Длина 
= 
* 
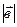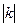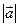2. направление вектора 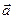совпадает с направлением вектора в, если k>0 и протиположно направленный если k<0 .
Аналогично можно определить сумму нескольких векторов, например сумма четырех векторов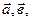 
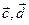будет вектор 
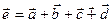начало которого совпадет сначалом вектора 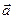, а конец с концом вектора 
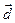( правило многоугольника).
Сумма векторов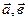 
и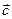 
,не лежащих в одной или паралельных плоскостях, есть вектор 
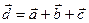определяемый диагональю параллепипеда построенного ан векторах 
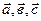(правило параллелпипеда).
Разность векторов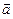 
и 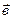есть вектор равный сумме вектора 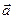и вектора противоположного вектору 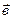т.е. ( - ).
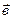Если на векторах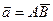 
и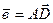 
построен параллелограмм, то одна диагональ есть сумма, а вторая 
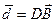есть их разность.
Если на множестве определены две операции, которые удовлетворяют законам сложения и умножения на число, тотакое множество называется векторным пространством.
Система векторов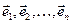 
называется базисом векторного пространства, если она удовлетворяет условиям:
- система векторов линейно независима
- любой вектор векторного пространства линейно выражается через эти вектора
Число векторов базиса называется размерностью пространства.
Разложение вектора по базисным векторам имеет вид: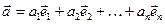 
, здесь коэффициенты перед базисными векторами называются координатами вектора. В двумерном пространстве вектор 
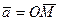имеет координаты- 
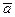={х,y}, а в трехмерном пространстве 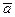= {х,у,z}.
Тогда для векторов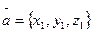 
и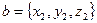 
координаты суммы и разности будут определятся соответственно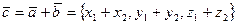 
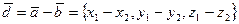(1)
А координаты произведения вектора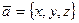 
на число λ будут 
.
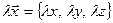б) Скалярное произведение векторов.