2 тема : Система линейных уравнений.

Дата: 2025-05-25; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Система n линейных уравнений c n неизвестными имеет вид:

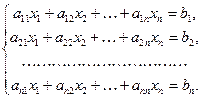(1)

Решением системы уравнений называется всякая совокупность чисел a_1, a_2, a_n, которая, будучи поставлена в систему на место неизвестных X _1,X _{2 ,…,}X _n, обращает все уравнения системы в тождество.

Система уравнений называется совместной, если она имеет одно единственное решение, и несовместной, если не имеет решений.

Совместная система уравнений называется определенной, если она имеет одно единственное решение, и неопределенной, если она имеет, по крайней мере, два различных решения.

Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и тоже множество решений.

Определителем системы называется определитель, составленный из коэффициентов a_ij.

Линейное уравнение называется однородным, если его свободный член равен нулю.

Система линейных уравнений называется однородной, если все входящие в неё уравнения являются линейными однородными уравнениями.

Однородная система n линейных уравнений с n неизвестными имеет ненулевые решения тогда и только тогда, когда определитель её равен нулю.

Для нахождения решения системы линейных уравнений применяют метод Гаусса и правило Крамера.

Метод Гаусса решения системы заключается в последовательном исключении переменных.

Теорема: Для того, чтобы система линейных неоднородных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу её основной матрицы.

Пусть дана система двух линейных уравнений с двумя неизвестными. Тогда:

1. если r = R =0, т.е. если все коэффициенты a₁ ,a ₂, b₁ ,b ₂, c _1, c₂ равны нулю, то любая пара действительных чисел является решением системы.
2. если r =0, R =1, т.е. a₁ =a ₂=b₁ =b ₂=0 и c + c≠0, то система не имеет решений.
3. если r =1, R =1, то система имеет бесконечно много решений, но не любая пара действительных чисел есть её решение.
4. если r =1, R =2, то система не имеет решений.
5. если r =2, R =2, то система имеет единственное решение, которое можно найти по правилу Крамера.

Формулы Крамера имеют вид: 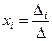.