1 тема : Матрицы и определители
Таблицу вида
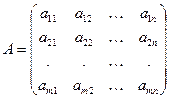называют прямоугольной матрицей размера 
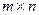. Элементы 
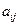назыаются элементами матрицы. m – число строк, n- число столбцов. Матрица размера 
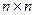называется квадратной матрицей.
Операции над матрицами определяются с помощью операции над их элементами.
- Две матрицы А и В размера 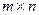равны, если равны их элементы
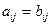. - Суммой матриц А и В размера 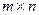есть матрица размера 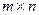, каждый ее элемент равен сумме соответствующих элементов.
- Произведение матрицы А размера 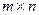на число есть матрица размера 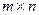, каждый элемент которой равен произведению 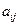на число.
- Произведение матрицы А размера 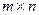на матрицу В размера
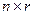есть матрица С размера 
.
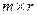Матрицей обратной для А называется матрица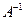 
, для которой 
.
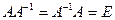Квадратная матрица называется невырожденной, если она имеет обратную матрицу.
Число линейно независимых строк(или столбцов) матрицы называют ее рангом.
Определителем квадратной матрицы А n-го порядка называют число
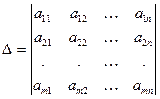(2)
Минором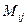 
элемента 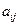в определителе n-го порядка (2) есть определитель
(n—1)-го порядка, получающийся из определителя (2), если из него вычеркнуть i-строку и j-й столбец.
Алгебраическое дополнение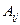 
элемента 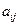есть коэффициент при 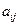в разложении определителя или 
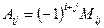. Определитель можно выразить через элементы его строки или столбца и их алгебраические дополнения следующим образом: 
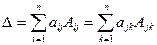(разложение Лапласа).
Определитель второго порядка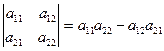 
.
Определитель третьего порядка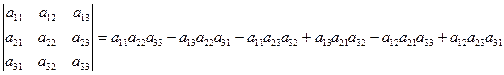 
.
Свойства определителей
- Определитель не меняется при транспонировании
- При перемене местами двух строк(столбцов) определитель меняет знак.
- Если квадратная матрица содержит две одинаковые строки (столца), то ее определитель равен нулю.
- Если все элементы какой –либо строки (столбца) определителя умножить на число с, то на это число умножится и сам определитель.
- Если элементы любой строки(столбца) представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, в первом из которых элементы отмеченной строки равны первым слагаемым, во втором –вторым.
- Определитель не меняется при строчном (столбцевом) перобразовании
- Сумма произведении элементов любой строки(столбца) на алгебраические дополнения элементов другой строки(столбца) равна нулю.
Если все элементы определителя n-го порядка расположенные выше (или ниже) главной диагонали равны 0, то определитель равен произведению элементов расположенных на главной диагонали.