1. Вероятность суммы несовместных событий
ПЛАН ЗАНЯТИЯ
Дисциплина: ЕН.03 Теория вероятностей и математическая статистика
Преподаватель: Старченко Е.А
Курс: 3
Группа: 1 ПКС-20
Специальность: 09.02.03 Программирование в компьютерных системах»
Дата: 28.09.22
Время проведения: 11.50-13.20, 3 пара
Тема: Сумма событий. Вероятность суммы событий
Цель занятия:
дидактическая: Научиться находить вероятность суммы случайных событий.
развивающая: развивать абстрактное мышление, логику
Вид занятия лекция
Литература
Теория вероятностей и математическая статистика : учеб. пособие / Е. А. Трофимова, Н. В. Кисляк, Д. В. Гилёв ; [под общ. ред. Е. А. Трофимовой] ; М-во образования и науки Рос. Федерации, Урал. федер. ун-т. – Екатеринбург : Изд-во Урал. ун-та, 2018, стр. 25
Интернет-ресурсы:
https://www.matburo.ru/tv_spr_sub.php?p=1
ЗАДАНИЕ: законспектировать лекцию, ответить на контрольные вопросы и решить задачу. Работы в электронном виде отправить для проверки.
КОНСПЕКТ ЛЕКЦИИ
План.
1. Вероятность суммы несовместных событий
2. Вероятность суммы совместных событий.
К сожалению, на практике далеко не всегда для подсчета вероятности достаточно формул классической и геометрической вероятностей. Часто приходится прибегать к более сложным конструкциям. Для облегчения подсчета используются несколько теорем вероятностей.
1. Вероятность суммы несовместных событий
Сформулируем теорему(правило) сложения вероятностей.
Теорема 1. Если два события А и В несовместны, тогда вероятность суммы конечного числа событий равна сумме вероятностей этих событий:
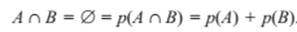
П р и м е р
1) А = {сдать теорию вероятностей на «5»};
B = {сдать теорию вероятностей на «4»};
р(А) = 0,1; р(В) = 0,3 Р(А + В) = 0,1 + 0,3 = 0,4.
2) А = {сдать теорию вероятностей на «5»};
B = {сдать статистику на «5»};
р(А) = 0,6; р(В) = 0,8, значит, p(А + В) = 1,4 , что недопустимо, так как вероятность не может быть больше 1.
Эти события совместны, так как можно сдать и теорию вероятностей, и статистику, теорема 1 не работает.
Следствие. Сумма вероятностей событий, образующих полную группу, равна 1, т.е.
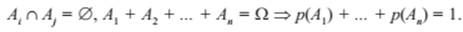
Доказательство
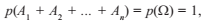
но так как события независимы, то по теореме 1:
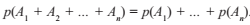
Следствие. Вероятность противоположного события равна 1 – вероятность события А, т.е.
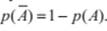
П р и м е р
А = {сдать методы оптимальных решений};
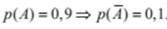
2. Вероятность суммы совместных событий
Теорема 2. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления: Р(А + В) = Р(А)+ Р(В) – Р(АВ).
Для доказательства этой теоремы необходимо использовать вероятность произведения двух случайных событий, т.е. исключить одновременное наступление событий.
Контрольные вопросы
1. Какие события называются несовместными?
2. Чему равна вероятность сумму двух несовместных событий?
3. Какие следствия из этого вытекает?
4. Какие события называются совместными?
5. Чему равна вероятность сумму двух совместных событий?
6. Решить задачу. Вероятность выхода изделия из строя при эксплуатации сроком до одного года равна 0,13, а при эксплуатации сроком до 3 лет-0,36. Найти вероятность выхода изделий при эксплуатации сроком от 1 года до 3 лет.








