Квадрат суммы и разности двух выражений
26. 12. 2022 г. 7 класс. Алгебра.
Квадрат суммы и разности двух выражений
1. Формула квадрата суммы
2. Формула квадрата разности
3. Примеры
Формула квадрата суммы
Возведем в квадрат сумму (a+b):
(a+b)2=(a+b)(a+b)=a(a+b)+b(a+b)=a2+ab+ab+b2=a2+2ab+b2
Мы получили формулу квадрата суммы двух выражений:
(a+b)2=a2+2ab+b2
Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.
Формула помогает нам избавиться от лишней работы: не перемножать скобки каждый раз и не приводить постоянно подобные, получая из четырёх слагаемых три.
Вместо a и b в формуле могут быть любые одночлены (и даже многочлены), которые нужно подставить. Поэтому в правиле и говорится о «выражениях», а не просто о «переменных». Например:
(5x2+7y)2=(5x2)2+2⋅5x2⋅7y+(7y)2=25x2+70x2y+49y2
Геометрическое объяснение
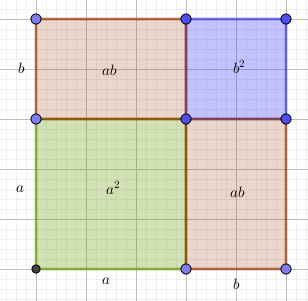
Рассмотрим квадрат со стороной (a+b). Он состоит из двух квадратов и двух прямоугольников. Для площади можем записать:S=(a+b)2=a2+b2+2ab
Откуда(a+b)2=a2+2ab+b2
И формула квадрата суммы замечательно подтверждается геометрическими соображениями.
Формула квадрата разности
Теперь возведём в квадрат разность:
(a−b)2=(a−b)(a−b)=a(a−b)−b(a−b)=a2−ab−ab+b2=a2−2ab+b2
Мы получили формулу квадрата разности двух выражений:
(a−b)2=a2−2ab+b2
Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого и второго выражения, плюс квадрат второго выражения.
Геометрическое объяснение
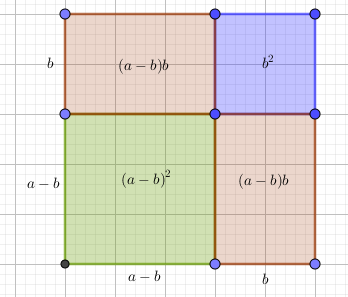
Рассмотрим квадрат со стороной a, в один из углов которого вписан квадрат поменьше со стороной b<a.
Для его площади можем записать:a2=(a−b)2+b2+2(a−b)bОткуда(a−b)2=a2−b2−2(a−b)b=a2−b2−2ab+2b2=a2−2ab+b2
И формула квадрата разности также подтверждается геометрией.
Внимание!
Не забывайте о втором слагаемом в формулах квадрата двучленов!
Не путайте знаки «+» и «-» перед слагаемыми!
Неправильно: (a+b)2 ≠ илиa2+b2или(a−b)2≠a2−b2
Правильно: (a+b)2=a2+ 2ab и+b2и(a−b)2=a2 -2ab+b2
Примеры
Пример 1. Найдите квадрат суммы:
а) (x+y)2=x2+2xy+y2
б) (3+t)2=32+2⋅3t+t2=9+6t+t2
в) (3a+4b)2=(3a)2+2⋅3a⋅4b+(4b)2=9a2+24ab+16b2
г) (4k2m+5n)2=(4k2m)2+2⋅4k2m⋅5n+(5n)2=16k4m2+40k2mn+25n2
Пример 2. Найдите квадрат разности:
а) (m−n)2=m2−2mn+n2
б) (x−5)2=x2−2x⋅5+52=x2−10x+25
в) (7y−9z)2=(7y)2−2⋅7y⋅9z+(9z)2=49y2−126yz+81z2
г) (3km2−8n2)2=(3km2)2−2⋅3km2⋅8n2+(8n2)2=9k2m4−48km2n2+64n4
Пример 3. Выполните действия:
а) (10m−1)2+20m=(10m)2−2⋅10m⋅1+1+20m=
=100m2−20m+1+20m=100m2+1
б) 36k2−(1−6k)2=36k2−(1−2⋅6k+(6k)2)=36k2−1+12k−36k2=12k−1
в) 4(x−1)−(2x+1)2=4x−4−((2x)2+2⋅2x+1)=4x−4−4x2−4x−1=−4x2−5
г) 13(3y+4)2−8y=13((3y)2+2⋅3y⋅4+42)−8y=13(9y2+24y+16)−8y=
=3y2+8y+163−8y=3y2+513
Пример 4. Решите уравнение:
а) (7−x)2−(x+8)2=45
49−14x+x2−(x2+16x+64)=45
49-14x-16x-64 = 45
-30x = 45-49+64
-30x = 60
x = -2
б) (2x−15)2−x(4x+3)=153
(2x)2−2⋅2x⋅15+152−4x2−12x=153
-60x+225-12x = 153
-72x = 153-225
-72x = -72
x = 1








