1.11 Экономические индексы
1.11.1 Понятие экономических индексов и их классификация
Индексы относятся к важнейшим обобщающим показателям. «Индекс» в переводе с латинского - указатель или показатель. Он используется как понятие в математике, экономике, в метеорологии и других науках.
В статистике индексом называют относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве или дает сравнение фактических данных с любым эталоном (план, прогноз, норматив и т.д.).
Как относительная величина индекс выражается в форме коэффициента, либо в процентах или промилле. Название индекса отражает его социально-экономическое содержание, а числовое значение – интенсивность изменения или степень отклонения.
Индексы выполняют две функции:
§ синтетическую – используется как обобщающая характеристика изменения явления;
§ аналитическую – служит для изучения влияния отдельных факторов на изменение явления.
Большинство индексов выполняет обе функции одновременно.
В целом индексный метод направлен на решение следующих задач:
1) характеристика общего изменения уровня сложного социально-экономического явления;
2) анализ влияния каждого из факторов на изменение индексируемой величины путем элиминирования воздействия прочих факторов;
3) анализ влияния структурных сдвигов на изменение индексируемой величины.
В международной практике индексы принято обозначать символами i и I. Буквой «i» обозначаются индивидуальные (частные) индексы, буквой «I» - общие индексы. Подстрочный знак внизу справа означает период: 0 – базисный; 1 – отчетный.
Используются определенные символы для обозначения индексируемых показателей:
p - цена;
q - количество;
p q – стоимость продукции или товарооборот;
z - себестоимость;
z q – издержки производства;
t – трудоемкость;
t q – затраты рабочего времени на производство продукции.
Классификация индексов:
1. По степени обобщения данных:
§ индивидуальные;
§ сводные (общие);
2. По форме построения:
§ агрегатные;
§ средние: - арифметические;
- гармонические;
3. По отношению ко времени:
§ динамические индексы: - цепные;
- базисные;
§ территориальные;
4. По виду весов:
§ индексы с переменными весами;
§ индексы с постоянными весами;
5. В зависимости от структуры совокупности:
§ индексы переменного состава;
§ индексы постоянного состава.
Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту:
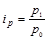 - индекс цены, (1.11.1)
- индекс цены, (1.11.1)
где 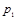 - цена товара в текущем периоде;
- цена товара в текущем периоде;
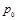 - цена товара в базисном периоде;
- цена товара в базисном периоде;
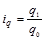 - индекс физического объема реализации; (1.11.2)
- индекс физического объема реализации; (1.11.2)
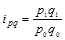 - индекс товарооборота (1.11.3)
- индекс товарооборота (1.11.3)
Например, если цена товара А в текущем периоде составляла 45 руб., а в базисном – 37,5 руб., то индивидуальный индекс цены будет равен:
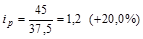
Индивидуальные индексы, в сущности, представляют собой относительные показатели динамики или темпы роста, и по данным за несколько периодов времени могут рассчитываться в цепной или базисной формах.
1.11.2 Агрегатные и средние индексы
В тех случаях, когда исследуются не единичные объекты, а состоящие из нескольких элементов совокупности, используются сводные индексы. Исходной формой сводного индекса является агрегатная.
Агрегатный индекс – это сложный относительный показатель, служащий для соизмерения явления, составные части которых непосредственно несоизмеримы.
Сводный индекс товарооборота:
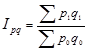 (1.11.4)
(1.11.4)
Показывает во сколько раз увеличится или уменьшится товарооборот отчетного периода по сравнению с базисным.
Для иллюстрации этого и последующих индексов воспользуемся следующими условными данными (табл. 1.11.1):
Таблица 1.11.1
Цены и объем реализации трех товаров
| Товар | Сентябрь | Октябрь | ||
цена,
руб.
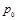
| продано, тыс. шт.
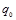
| цена,
руб.
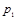
| продано, тыс. шт.
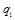
| |
| А Б В | 20 55 44 | 22 12 13 | 17 44 39 | 31 14 13 |
Рассчитаем индекс товарооборота:
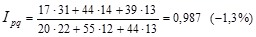
Таким образом, товарооборот в целом по данной товарной группе в текущем периоде по сравнению с базисным уменьшился на 1,3%.
Отметим, что размер товарной группы при расчете этого и последующих индексов значения не имеет.
На величину полученного индекса товарооборота оказывают влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких показателей как цена и себестоимость физический объем реализации обычно фиксируют на уровне текущего периода. Таким способом получают сводный индекс цен (по методу Пааше):
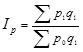 (1.11.5)
(1.11.5)
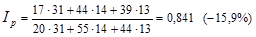
По данной товарной группе цены в октябре по сравнению с сентябрем снизились на 15,9%.
При построении данного индекса цена выступает в качестве индексируемой величины, а количество проданного товара – в качестве веса. Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую каким, был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий отражает имевшее место изменение цен.
Числитель и знаменатель сводного индекса цен также можно интерпретировать и по-другому. Числитель представляет собой сумму денег, фактически уплаченных покупателями за товары в текущем периоде. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии, если знак «-» или перерасхода, если знак «+», покупателей от изменения цен:
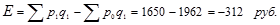
Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения. Весами в данном случае выступают цены, которые фиксируются на базисном уровне:
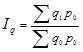 (1.11.6)
(1.11.6)
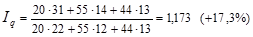
Физический объем реализации (товарооборота) увеличился на 17,3%.
Между рассчитанными индексами существует следующая взаимосвязь:
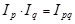 (1.11.7)
(1.11.7)
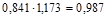
Мы рассмотрели применение индексного метода в анализе товарооборота и цен. Однако эта же индексная система может использоваться для анализа результатов производственной деятельности предприятий, выпускающих разнородную продукцию. Тогда приведенные выше индексы соответственно называются:
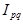 - индекс стоимости продукции;
- индекс стоимости продукции;
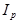 - индекс оптовых цен;
- индекс оптовых цен;
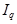 - индекс физического объема продукции.
- индекс физического объема продукции.
Взаимосвязь между этими индексами остается прежней:
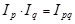
В ряде случаев на практике вместо индексов в агрегатной форме удобнее использовать средние арифметические и средние гармонические индексы. Любой сводный индекс можно представить как среднюю взвешенную из индивидуальных индексов. Однако при этом форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу.
Предположим, мы располагаем данными о стоимости проданной продукции в текущем периоде и индивидуальными индексами цен, полученными, например, в результате выборочного наблюдения. Тогда при расчете сводного индекса цен можно использовать следующую замену:
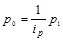
В целом же сводный индекс цен в данном случае будет выражен в форме средней гармонической:
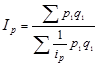 (1.11.8)
(1.11.8)
Рассмотрим следующий условный пример (табл. 1.11.2):
Таблица 1.11.2
Данные о реализации и ценах по товарной группе
| Товар | Реализация в текущем периоде, руб. | Изменение цен в текущем периоде по сравнению с базисным, % |
| А Б В | 330 310 390 | +3,0 -2,0 0 |
Данные последней графы таблицы отражают изменение индивидуальных индексов цен, которые по товарам А, Б и В соответственно равны 1,03; 0,98 и 1,0.
С учетом этого получим:
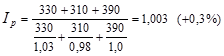
Цены по данной товарной группе в среднем возросли на 0,3%.
При расчете сводного индекса физического объема товарооборота можно использовать среднеарифметическую форму. При этом производится замена:
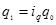
Тогда индекс имеет вид:
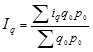 (1.11.9)
(1.11.9)
Для иллюстрации этой формы расчета воспользуемся следующим примером (табл. 1.11.3):
Таблица 1.11.3
Данные о реализации трех товаров в натуральном и
стоимостном выражении
| Товар | Реализация в базисном периоде, руб. | Изменение физического объема реализации в текущем периоде по сравнению с базисным, % |
| А Б В | 467 274 518 | -6,5 -8,3 +1,5 |
Индивидуальные индексы физического объема будут равны 0,935; 0,917; 1,015. С учетом этого рассчитаем среднеарифметический индекс:
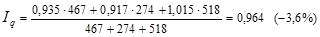
Физический объем реализации данных товаров в среднем снизился на 3,6%.
1.11.3 Индексный анализ взвешенной средней. Индекс
структурных сдвигов
При анализе динамики взвешенной средней используется система индексов, включающая:
1) индекс переменного состава;
2) индекс структурных сдвигов;
3) индекс фиксированного состава.
В предыдущих задачах рассматривались индексы, рассчитываемые по нескольким товарам или видам продукции, реализуемым или производимым в одном месте. Рассмотрим теперь случай, когда один товар или вид продукции реализуется или производится в нескольких местах (табл. 1.11.4):
Таблица 1.11.4
Реализация товара А в двух регионах
| Регион | Сентябрь | Октябрь | ||
цена,
руб.
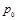
| продано, тыс. шт.
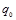
| цена,
руб.
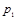
| продано, тыс. шт.
| |
| 1 2 | 16 22 | 130 260 | 17 25 | 234 117 |
Так как в данном случае реализуется один и тот же товар, вполне правомерно рассчитать его среднюю цену за сентябрь и за октябрь. Сравнением полученных средних значений получают индекс цен переменного состава:
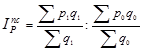 (1.11.10)
(1.11.10)
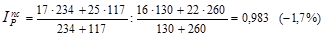
Из таблицы видно, что цена в каждом регионе в октябре по сравнению с сентябрем возросла. В целом же средняя цена снизилась на 1,7%. Такое несоответствие объясняется влиянием изменения структуры реализации товаров по регионам: в сентябре по более высокой цене продали товара вдвое больше, в октябре ситуация принципиально изменилась (в данном условном примере для наглядности числа подобраны таким образом, чтобы это различие в структуре продаж было очевидным). Оценить воздействие этого фактора можно с помощью индекса структурных сдвигов:
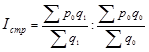 (1.11.11)
(1.11.11)
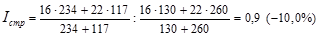
Первая формула в этом индексе позволяет ответить на вопрос, какой была бы средняя цена в октябре, если бы цены в каждом регионе сохранились на прежнем сентябрьском уровне. Вторая часть формулы отражает фактическую среднюю цену сентября. В целом по полученному значению индекса мы можем сделать вывод, что за счет структурных сдвигов цены снизились на 10,0%.
Последним в данной системе является индекс цен фиксированного состава, который не учитывает влияние структуры:
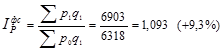 (1.11.12)
(1.11.12)
Итак, если бы структура реализации товара А по регионам не изменилась, средняя цена возросла бы на 9,3%. Однако, влияние на среднюю цену первого фактора оказалось сильнее, что отражается в следующей взаимосвязи:
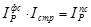 (1.11.13)
(1.11.13)
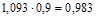
Аналогично строятся индексы структурных сдвигов, переменного и фиксированного состава для анализа изменения себестоимости, трудоемкости и пр.
1.11.4 Важнейшие экономические индексы и
их взаимосвязи
Между важнейшими индексами существуют взаимосвязи, позволяющие на основе одних индексов получить другие. Зная, например, значение цепных индексов за какой-либо период времени, можно рассчитать базисные индексы. И наоборот, если известны базисные индексы, то путем деления одного из них на другой можно получить цепные индексы.
Существующие взаимосвязи между важнейшими индексами позволяют выявить влияние различных факторов на изменение изучаемого явления, например, связь между индексом стоимости продукции, физического объема продукции и цен (1.11.2). Другие индексы также связаны между собой.
Так, индекс издержек производства – это произведение индекса себестоимости продукции и индекса физического объема продукции:
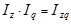 (1.11.14)
(1.11.14)
или
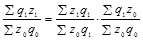 (1.11.15)
(1.11.15)
Индекс затрат времени на производство продукции может быть получен в результате умножения индекса физического объема продукции и величины, обратной величине индекса трудоемкости, то есть индекс производительности труда:
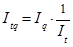 (1.11.16)
(1.11.16)
или
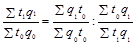 (1.11.17)
(1.11.17)
Существует важная взаимосвязь между индексами физического объема продукции и индексами производительности труда.
Индекс производительности труда рассчитывается на основе следующей формулы:
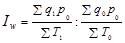 (1.11.18)
(1.11.18)
то есть представляет собой отношение средней выработки продукции (в сопоставимых ценах) в единицу времени (или на одного занятого) в текущем и базисном периодах.
Индекс физического объема продукции равен произведению индекса производительности труда на индекс затрат рабочего времени (или численности занятых):
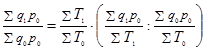 (1.11.19)
(1.11.19)
Взаимосвязь между отдельными индексами может быть использована для выявления влияния отдельных факторов, оказывающих воздействие на изучаемое явление.
1.11.5 Особенности расчетов индексов цен
В рыночном хозяйстве особое место среди индексов качественных показателей отводится индексам цен. Основным назначением индекса цен является оценка динамики цен на товары производственного и непроизводственного потребления. Кроме этого используется при корректировке законодательно устанавливаемого минимального размера оплаты труда и установлении ставок налогов.
Рассмотрим основные формулы расчета индексов цен:
§ Индекс Пааше: 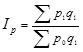 ; (1.11.20)
; (1.11.20)
§ Индекс Ласпейреса: 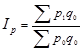 ; (1.11.21)
; (1.11.21)
§ Индекс Фишера: 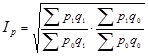 ; (1.11.22)
; (1.11.22)
§ Индекс Эджворта – Маршалла: 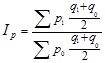 (1.11.23)
(1.11.23)
Индексируемой величиной индексов являются цены. Весами же в индексе цен Пааше выступает количество продукции текущего периода, а в индексе цен Ласпейреса – количество продукции базисного периода.
Формула индекса цен Ласпейреса применяется в расчетах индекса потребительских цен, формула индекса цен Пааше - при расчете индекса-дефлятора ВВП.
Значения индексов цен Пааше и Ласпейреса не совпадают. Отличие значений объясняется тем, что индексы имеют различное экономическое содержание.
Индекс цен, исчисленный по формуле Пааше, дает ответ на вопрос, насколько товары в текущем периоде стали дороже (дешевле), чем в базисном. Индекс цен Ласпейреса показывает, во сколько бы раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетный период.
Согласно практике индекс цен, рассчитанный по формуле Пааше, имеет тенденцию некоторого занижения, а по формуле Ласпейреса – завышения темпов инфляции. Подобная систематическая связь индексов носит название эффекта Гершенкрона.
Индекс Фишера в силу сложности расчета и трудности экономической интерпретации на практике используется довольно редко. Чаще всего он применяется в расчетах паритетах покупательной способности валют.
Тренировочные задания
1. Известны следующие данные о реализации фруктов предприятиями розничной торговли округа:
| Товар | Цена за 1 кг, руб. | Продано, ц | ||
июль
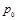
| август
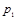
| июль
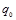
| август
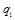
| |
| Яблоки Груши | 20 25 | 18 20 | 17,5 10,5 | 27,7 14,5 |
Рассчитайте сводные индексы:
а) товарооборота;
б) цен;
в) физического объема реализации.
Определите абсолютную величину экономии покупателей от снижения цен.
Решение:
а) сводный индекс товарооборота - это сравнение товарооборота в текущем периоде с его величиной в базисном периоде:
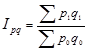 ;
;
б) сводный индекс цен (по методу Пааше) – это сравнение товарооборота в текущем периоде с его величиной в базисном периоде при условии сохранения цен на базисном уровне:
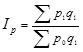 ;
;
в) сводный индекс физического объема реализации характеризует изменение количества проданных товаров в физических единицах измерения:
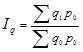 .
.
Воспользуемся вспомогательными расчетными графами:
| Расчетные графы | ||
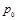 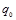
| 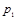 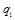
| 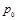 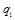
|
| 350,0 262,5 | 498,6 290,0 | 554,0 362,5 |
| 612,5 | 788,6 | 916,5 |
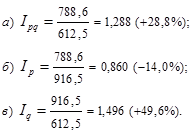
Проверим:
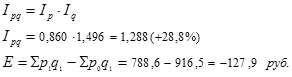
Это экономия (т.к. знак «-»; если знак «+», то это перерасход) покупателей от изменения цен.
2. Имеются следующие данные о реализации картофеля на рынках города:
|
Рынок
| Апрель | Май | ||
Цена за 1 кг,
руб.
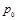
| Продано, ц
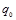
| Цена за 1кг,
руб.
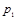
| Продано, ц
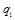
| |
| 1 2 | 10,0 12,0 | 45,1 32,0 | 14,0 15,0 | 37,4 21,9 |
| Итого | - | 77,1 | - | 59,3 |
Рассчитайте:
а) индекс цен переменного состава;
б) индекс цен фиксированного состава;
в) индекс структурных сдвигов.
Решение:
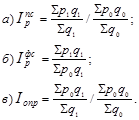
| Расчетные графы | ||
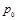 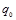
| 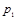 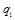
| 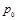 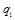
|
| 451,0 384,0 | 523,6 328,5 | 374,0 262,8 |
| 835,0 | 852,1 | 636,8 |
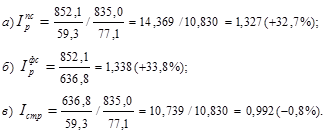
3. Изменение объема ВВП по кварталам в 2003-2004 гг. в РФ характеризуется следующими данными:
| Год, квартал | ВВП, млрд. руб. |
| 2003 I II III IV 2004 I II III IV | 2869 3103 3567 3662 3528 3938 4590 4723 |
// «Вопросы статистики» №6/2005, с.73
Определите общее изменение объема ВВП за весь рассматриваемый период.
4. В результате внедрения мероприятия по модернизации оборудования объем реализации цемента одного из заводов региона в натуральном выражении в отчетном периоде по сравнению с базисным возрос на 8,7%, при этом индекс цен на цемент составил 90,2%. Определите изменение товарооборота.
5. Как изменились общие затраты труда на предприятии, если стоимость продукции в сопоставимых ценах возросла на 15,1%, а производительность труда повысилась на 4,7%?
6. Имеются следующие данные о реализации овощей на городском рынке:
| Продукты | Апрель | Май | ||
| Цена за 1кг, руб. | Продано, ц | Цена за 1кг, руб. | Продано, ц | |
| Лук Огурцы Помидоры | 15 55 60 | 14,5 20,1 10,8 | 11 40 55 | 16,4 22,8 15,6 |
Рассчитайте сводные индексы цен, физического объема реализации и товарооборота.
7. Определите индекс розничных цен за I квартал текущего года, если известно, что цены на продовольственные товары увеличились на 17%, а на промышленные – на 9%. Товарная структура розничного товарооборота в I квартале: продовольственные товары – 46%; промышленные – 54%. Как изменилась покупательная способность денежной единицы?
8. Имеются следующие данные о себестоимости и объемах производства продукции промышленного предприятия:
| Изделие | 2003 | 2004 | ||
| Себестоимость единицы продукции, руб. | Произведено, тыс. шт. | Себестоимость единицы продукции, руб. | Произведено, тыс. шт. | |
| 001 002 003 | 253 128 97 | 59,2 54,1 102,6 | 284 230 101 | 56,7 50,1 104,7 |
Определите:
а) индивидуальные и сводные индексы себестоимости;
б) сводные индексы физического объема продукции;
в) сводный индекс затрат на производство.
Покажите взаимосвязь сводных индексов.
9. Имеются следующие условные данные по предприятию:
| Вид продукции | Произведено, тыс. шт. | Среднесписочное число рабочих, чел. | Оптовая цена продукции в 2002 г., тыс. руб. | ||
| 2002 | 2003 | 2002 | 2003 | ||
| 1 2 | 29,3 33,9 | 30,1 33,6 | 1420 1270 | 1500 1350 | 85 64 |
Определите:
а) индекс физического объема продукции;
б) индекс производительности труда;
в) индекс затрат труда.
10. На предприятии числится 2 группы рабочих. По данным таблицы определите индекс средней заработной платы:
| Группа рабочих | I квартал | II квартал | ||
| Общие затраты времени, чел-ч. | Фонд заработной платы, тыс. руб. | Общие затраты времени, чел-ч. | Фонд заработной платы, тыс. руб. | |
| 1 2 | 1260 140 | 505 47 | 1652 158 | 696 77,5 |
11. Затраты на радиорекламу отдельных категорий товара характеризуются следующими изменениями:
| Категория товара | Себестоимость одного рекламного ролика, тыс. руб. | Количество изготовленных роликов, ед. | ||
| Базисный период | Отчетный период | Базисный период | Отчетный период | |
| А Б В | 2,54 2,24 2,10 | 2,92 2,70 2,46 | 147 145 139 | 170 136 150 |
Определите:
1) сводные индексы себестоимости рекламных роликов;
2) сводные индексы количества изготовленных рекламных роликов;
3) абсолютный размер перерасхода (экономии) в общих затратах на радиорекламу за счет изменения себестоимости.
Проанализируйте полученные результаты.
Тест
1. Индексы используются для характеристики динамики социально-экономических процессов и явлений:
а) во времени;
б) в пространстве;
в) во времени и в пространстве.
2. Индивидуальные индексы могут быть:
а) цепными или базисными;
б) средними.
3. Сводные индексы позволяют получить обобщающую оценку изменения:
а) по товарной группе;
б) одного товара за несколько периодов.
4. Средний индекс физического объема продукции рассчитывается по формуле:
а) средней арифметической;
б) средней гармонической;
в) средней геометрической;
г) средней квадратической.
5. Может ли индекс переменного состава превышать индекс фиксированного состава?
а) может;
б) не может.
6. Денежные затраты на строительно-монтажные работы увеличились в текущем периоде на 38%, а себестоимость работ – 46,8%. Определите индекс физического объема строительно-монтажных работ.
а) 2,05;
б) 0,94;
в) 0,81;
г) 1,06.
7. Рассчитайте общий индекс физического объема продукции по следующим данным:
| Изделия | Изменения выпуска в отчетном периоде по сравнению с базисным, % | Удельный вес изделия в общем выпуске базисного периода, % |
| А Б | +10 -10 | 60 40 |
а) 100%;
б) 102%;
в) 116 %;
г) 103%.
8. Стоимость произведенной продукции в действующих ценах выросла за год на 8%. Цены за этот же период снизились на 2%. Как изменился физический объем продукции?
а) увеличится на 16%;
б) увеличится на 5,8%;
в) увеличится на 10,2%.
9. При построении индекса цен Пааше в качестве весов используются:
а) количество продукции текущего периода;
б) количество продукции базисного периода;
в) среднее количество продукции.
10. Индекс цен, рассчитываемый по формуле Ласпейреса:
а) имеет тенденцию некоторого занижения темпов инфляции;
б) имеет тенденцию некоторого завышения темпов инфляции;
в) отражает реальные темпы инфляции.
11. Индекс потребительских цен рассчитывается по формуле индекса:
а) Пааше;
б) Ласпейреса;
в) Фишера.
12. Динамика потребительских цен на отдельные товарные группы характеризуется следующими данными:
| Группа товаров | Товарооборот в фактических ценах, млн. руб. | Темп прироста цен, % | |
| Базисный период | Текущий период | ||
| Продовольственные Непродовольственные | 526 424 | 583 255 | +6 +2 |
Определите сводный индекс цен на товары в целом, %:
а) 104,0;
б) 105,6;
в) 104,75;
г) 104,92.
13. Индекс – дефлятор рассчитывается по формуле индекса цен:
а) Пааше;
б) Ласпейреса;
в) Фишера;
г) Лоу.
14. Сводный индекс производительности труда рассчитывается по формуле:
а) агрегатного индекса;
б) среднего гармонического индекса;
в) среднего арифметического индекса.
15. Определите индекс выработки продукции, если индекс трудоемкости составил 0,8:
а) 120%;
б) 125%;
в) 80%.
16. Рассчитайте индекс цен Фишера, если индекс Ласпейреса составляет 125%, а индекс цен Пааше – 122%;
а) 123,50%;
б) 152,50%;
в)123,49%;
г) 123,45%.
17. Себестоимость продукции в отчётном периоде по сравнению с базисным увеличилась на 14%, количество производимой продукции сократилось на 14%. Как изменилась величина издержек производства:
а) уменьшилась на 2%;
б) увеличилась на 2%;
в) не изменилась.
18. Эффект Гершенкрона объясняет:
а) систематическую связь индексов Пааше и Ласпейреса (первый, как правило, больше);
б) взаимосвязь индексов цен, физического объёма и стоимости продукции;
в) тождественность агрегатных и средних индексов.
19. Потребительские цены на товары и услуги увеличились в текущем году по сравнению с прошлым годом на 20%. Определите индекс покупательной способности денежной единицы.
а) 1,25;
б) 1,2;
в) 0,8;
г) 0,83.
20. Какие индексы обладают свойством мультипликативности:
а) цепные с переменными весами;
б) цепные с постоянными весами;
в) базисные с переменными весами.








