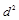Для определения рангового коэффициента Спирмена ( ) заполним графы 6 и 7 таблицы 1.9.10.
Подставим в формулу (1.9.23) данные графы 7 табл. 1.9.10, n = 15 и получим:
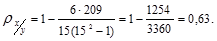
В итоге получили положительную дробь, причем значение ее больше, чем 0,5, что свидетельствует о существенной прямой связи между стоимостью основных производственных фондов и количеством выпущенного цемента.
,
Таблица 1.9.10
Расчетные данные для определения рангового
коэффициента Спирмена
| № п/п | Среднегодовая стоимость промышленно- производственных фондов, млн. руб. х | Выпуск цемента, тыс. т
у | Ранги | Раз- ность ран- гов
d | Квадрат раз- ности рангов
| |
|
| |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 11,1 8,4 8,0 7,9 5,3 10,3 8,0 8,7 12,8 5,4 5,8 3,6 5,5 4,5 2,9 | 8,8 22,3 19,8 20,8 11,5 25,8 22,8 15,7 21,7 10,7 12,2 8,5 13,9 14,5 7,6 | 14 11 9 8 4 13 10 12 15 5 7 2 6 3 1 | 3 13 10 11 5 15 14 9 12 4 6 2 7 8 1 | 11 -2 -1 -3 -1 -2 -4 3 3 1 1 0 -1 -5 0 | 121 4 1 9 1 4 16 9 9 1 1 0 1 25 0 |
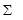
| - | - | - | - | - | 209 |
Ранговый коэффициент корреляции Кендалла (τ) также может использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты и ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле:
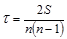 (1.9.24)
(1.9.24)
где n - число наблюдений;
S - сумма разностей между числом последовательностей и числом инверсий по второму признаку.
Расчет данного коэффициента выполняется в следующей последовательности:
1. Значения x ранжируются в порядке возрастания или убывания;
2. Значения y располагаются в порядке, соответствующем значениям x;
3. Для каждого ранга y определяется число следующих за ним значений рангов, превышающих его величину. Суммируя, таким образом, числа определяется величина P, как мера соответствия последовательностей рангов по x и y и учитывается со знаком (+);
4. Для каждого ранга y определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком (-);
5. Определяется сумма баллов по всем членам ряда.
В приведенном примере (таблица 1.9.10):
P = 14+13+7+9+9+7+7+4+4+1+1+2+0+1+0 = 79;
Q = 0+0+5+2+1+2+1+3+2+4+3+1+1+0+0 = 25;
Таким образом:
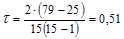 , что свидетельствует об умеренной связи между рассматриваемыми признаками.
, что свидетельствует об умеренной связи между рассматриваемыми признаками.
Как правило, коэффициент Кендалла меньше коэффициента Спирмена. При достаточно большом объеме совокупности значения данных коэффициентов имеют следующую зависимость:
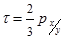
Связь между признаками признается статистически значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0,5.
Тренировочные задания
1. Имеются данные от Fortune о связи между оборотом и прибылью крупнейших компаний мира в 2004 г.:
| Компания | Оборот, млрд. долл. (x) | Прибыль, млрд. долл. (y) |
| 1. Wal Mart Stores | 288,0 | 10,3 |
| 2. BP | 285,1 | 15,4 |
| 3. Exxon Mobil | 270,8 | 25,3 |
| 4. Royal Dutch/Shell | 268,7 | 18,2 |
| 5. General Motors | 193,5 | 2,8 |
| 6. Daimler Chrysler | 176,7 | 3,1 |
| 7. Toyota Motor | 172,6 | 10,9 |
| 8. Ford Motor | 172,2 | 3,5 |
| 9. General Electric | 152,9 | 16,8 |
| 10. Total | 152,6 | 12,0 |
| Итого: | 2133,1 | 118,3 |
// «Эксперт» №28 (475), 2005
Составьте линейное уравнение регрессии. Вычислите параметры методом наименьших квадратов и сформулируйте выводы.
Решение:
Расчетные показатели представим в следующей таблице:
Расчетная таблица для определения параметров уравнения
регрессии в зависимости от оборота и прибыли компаний
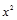
| 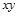
| 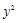
| 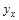
|
| 82944,00 | 2966,40 | 106,09 | 16,5 |
| 81282,01 | 4390,54 | 237,16 | 16,3 |
| 73332,64 | 6851,24 | 640,09 | 15,4 |
| 72199,69 | 4890,34 | 331,24 | 15,3 |
| 37442,25 | 541,80 | 7,84 | 10,6 |
| 31222,89 | 547,77 | 9,61 | 9,5 |
| 29790,76 | 1881,34 | 118,81 | 9,3 |
| 29652,84 | 602,70 | 12,25 | 9,3 |
| 23378,41 | 2568,72 | 282,24 | 8,1 |
| 23286,76 | 1831,20 | 144,00 | 8,0 |
| 484532,25 | 27072,05 | 1889,33 | 118,3 |
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
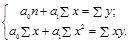
где n - объем исследуемой совокупности;
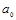 - показывает усредненное влияние на результативный признак неучтенных факторов;
- показывает усредненное влияние на результативный признак неучтенных факторов;
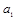 - коэффициент регрессии, показывает, на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.
- коэффициент регрессии, показывает, на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.
Решим систему:
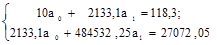
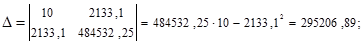
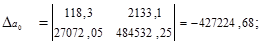
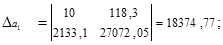
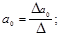
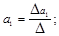
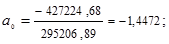
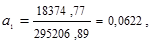
Отсюда: 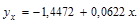
С увеличением оборота на 1 млрд. долл., прибыль компаний возрастает в среднем на 62,2 млн. долл.
2. При опросе жителей РФ предлагалось высказать свое мнение по следующим утверждениям:
1. Вступление в ВТО будет способствовать росту ВВП.
2. Вступление в ВТО никак не повлияет на рост ВВП.
Результаты обследования характеризуются следующими данными (чел.):
|
Варианты ответов | Количество опрашиваемых в возрасте, лет |
Всего | |
| 18-35 | 36-50 | ||
| Верно первое | 150 | 135 | 285 |
| Верно второе | 105 | 110 | 215 |
| Итого: | 255 | 245 | 500 |
Рассчитать коэффициенты ассоциации и контингенции.
Решение:
Воспользуемся вспомогательной таблицей для вычисления коэффициентов ассоциации и контингенции:
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
Коэффициенты вычисляются по следующим формулам:
ассоциации: 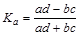 ;
;
контингенции: 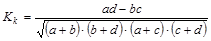 .
.
Причем, 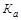 >
> 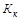 всегда. Связь считается подтвержденной, если
всегда. Связь считается подтвержденной, если 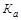
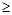 0,5 или
0,5 или 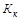
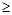 0,3.
0,3.
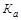 =
= 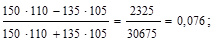
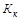 =
= 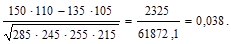
Вывод: так как 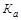 < 0,5 и
< 0,5 и 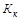 < 0,3 , то варианты ответов опрашиваемых не зависят от их возраста.
< 0,3 , то варианты ответов опрашиваемых не зависят от их возраста.
3. Имеются следующие данные о распределении школ города по типам и оценке сложности учебного предмета «Физика», тыс. человек:
| Тип школы | Хорошее освоение курса | Среднее освоение курса | Проблемы с освоением курса |
| Гимназия Лицей Колледж | 84,0 78,3 62,5 | 12,2 10,7 17,6 | 3,8 10,4 19,3 |
Рассчитайте коэффициенты взаимной сопряженности Пирсона и Чупрова. Сформулируйте выводы.
4. В результате проведённого обследования оценки уровня жизни работающих на предприятиях различных форм собственности было опрошено 250 респондентов. Результаты опроса представлены в следующей таблице:
| Форма собственности предприятия | Удовлетворённость уровнем жизни | Итого | |
| Вполне удовлетворён | Не удовлетворён | ||
| Бюджетная организация Частное предприятие | 88 25 | 125 12 | 213 37 |
| Итого | 113 | 55 | 250 |
Рассчитайте коэффициенты ассоциации и контингенции.
5. Имеются данные о связи между производством труб и выручкой предприятий российского трубного рынка в 2004 г.:
| № п/п | Производство труб, млн. тонн | Выручка, млн. долл. |
| 1 | 0,60 | 330 |
| 2 | 0,78 | 602 |
| 3 | 0,53 | 360 |
| 4 | 0,58 | 450 |
| 5 | 0,76 | 623 |
| 6 | 0,68 | 230 |
| 7 | 0,90 | 897 |
// «Эксперт» №3 (450), 2005
Вычислите ранговые коэффициенты Спирмена и Кендалла.
6. По 10 однородным предприятиям имеются следующие данные:
| № предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Количество рабочих с профессиональной подготовкой, % | 10 | 12 | 14 | 17 | 24 | 28 | 30 | 35 | 40 | 50 |
| Количество бракованной продукции, % | 18 | 17 | 14 | 12 | 10 | 10 | 8 | 9 | 6 | 6 |
По исходным данным постройте однофакторную регрессионную модель зависимости между выпуском бракованной продукции и профессиональной подготовкой рабочих.
Вычислите показатели тесноты корреляционной связи.
7. По 8 продовольственным магазинам имеются следующие данные:
| Товарооборот, тыс. руб. | 7 | 10 | 15 | 20 | 30 | 45 | 60 | 120 |
| Уровень издержек обращения по отношению к товарообороту, % | 10 | 9,0 | 7,2 | 6,0 | 6,3 | 5,8 | 5,4 | 5,0 |
Найдите уравнение корреляционной связи товарооборота и уровня издержек обращения.
Изобразите графически корреляционную связь.
Вычислите коэффициенты эластичности, показатели тесноты корреляционной связи.
8. Распределение предприятий по источникам средств для их покупки характеризуется следующими данными:
| Источник средств | Малый бизнес | Средний бизнес | Итого |
| Банковский кредит Собственные средства | 33 40 | 35 17 | 68 57 |
| Итого | 73 | 52 | 125 |
Вычислите коэффициенты ассоциации и контингенции. Какие выводы можно сделать на основании значений этих коэффициентов?
Тест
1. По направлению связи различают:
а) линейные;
б) прямые;
в) умеренные.
2. По аналитическому выражению связи бывают:
а) тесные;
б) криволинейные;
в) обратные;
г) сильные.
3. Функциональной является связь:
а) между двумя признаками;
б) при которой определенному значению факторного признака соответствует несколько значений результативного признака;
в) при которой определенному значению факторного признака соответствует одно значение результативного признака;
4. Аналитическое выражение связи определяется с помощью метода анализа:
а) корреляционного;
б) регрессионного;
в) группировок.
5. Коэффициент эластичности показывает:
а) на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%;
б) на сколько изменится в среднем значение результативного признака при увеличении факторного на единицу собственного измерения;
в) степень тесноты связи между результативным и факторным признаком;
г) степень вариации результативного признака.
6. С помощью каких показателей характеризуется теснота связи?
а) коэффициент детерминации;
б) коэффициент регрессии;
в) коэффициент корреляции.
7. Анализ тесноты и направления связей двух признаков осуществляется на основе:
а) частного коэффициента корреляции;
б) парного коэффициента корреляции;
в) множественного коэффициента корреляции;
г) частного коэффициента эластичности.
8. Отметьте правильное определение частной корреляции:
а) связь между двумя признаками;
б) зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
в) зависимость результативного и двух или более факторных признаков, включенных в исследование.
9. По следующим данным рассчитайте линейный коэффициент корреляции: 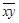 =4;
=4; 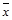 =2;
=2; 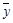 =1,5;
=1,5; 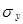 =0,5;
=0,5; 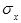 =4.
=4.
а)3;
б) 0,4;
в) 0,5;
г) 0,25.
10. Коэффициент корреляции показывает:
а) на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%;
б) на сколько изменится в среднем значение результативного признака при увеличении факторного на единицу собственного измерения;
в) степень тесноты связи между результативным и факторным признаком;
г) степень вариации результативного признака.
11. Множественный коэффициент корреляции изменяется в пределах:
а) от 0 до 1;
б) от -1 до 1.
12. Оценка значимости параметров модели регрессии осуществляется на основе:
а) коэффициента корреляции;
б) средней ошибки аппроксимации;
в) t – критерия Стьюдента.
13. Оценка значимости уравнения регрессии осуществляется на основе:
а) коэффициента детерминации;
б) F – критерия Фишера;
в) средней квадратической ошибки.
14. Мультиколлинеарность – это связь между:
а) признаками;
б) уровнями;
в) явлениями.
15. Определите величину коэффициента регрессии, если:
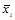 =20,
=20, 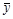 =10,
=10, 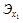 =0,8:
=0,8:
а) 1,6;
б) 0,4;
в) –1,6.
16. Коэффициент регрессии показывает:
а) на сколько %-тов в среднем изменится значение результативного признака при изменении факторного признака на 1%;
б) на сколько изменится в среднем значение результативного признака при увеличении факторного на единицу собственного измерения;
в) степень тесноты связи между результативным и факторным признаком.
17. Для оценки тесноты связи между альтернативными признаками можно использовать:
а) коэффициент корреляции рангов;
б) коэффициент ассоциации;
в) коэффициент детерминации;
г) корреляционное отношение.
18. Коэффициент взаимной сопряженности используют для оценки тесноты связи между признаками, если:
а) оба признака количественные;
б) только факторный признак атрибутивный;
в) только результативный признак атрибутивный;
г) оба признака атрибутивные.
19. Коэффициент корреляции рангов используется для оценки тесноты связи между:
1) количественными признаками;
2) признаками, значения которых можно упорядочить;
3) атрибутивными признаками.
а) 1;
б) 1,2;
в) 2;
г) 1,3.
20. Уравнение регрессии имеет вид 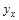 =7,1 + 1,5x. На сколько единиц своего измерения в среднем изменится у при увеличении х на одну единицу своего измерения:
=7,1 + 1,5x. На сколько единиц своего измерения в среднем изменится у при увеличении х на одну единицу своего измерения:
а) увеличится на 1,5;
б) уменьшится на 1,5;
в) увеличится на 3,0;
г) не изменится.
1.10 Статистическое изучение динамики социально-
экономических явлений
1.10. 1 Понятие рядов динамики и их классификация
Среди основных задач статистики важное место занимает описание изменений показателей во времени, изучение процесса развития, динамики социально-экономических явлений. Для отображения динамики строят ряды динамики (хронологические, временные).
Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологическом порядке числовых значений статистического показателя, характеризующих изменение общественных явлений во времени.
Составными элементами ряда динамики являются показатели уровней ряда - «y» и показатели времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени - «t».
Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно длительной динамике. На основную закономерность динамики накладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уровней, именуемой трендом, является одной из главных задач анализа рядов динамики.
Классификация рядов динамики:
1) В зависимости от характера временного параметра ряды делятся на:
§ моментные характеризуют значения показателя по состоянию на определенные моменты времени (см. табл. 1.10.1);
§ интервальные ряды динамики характеризуют значение показателя за определенные интервалы (периоды) времени (см. табл. 1.10.2).
Таблица 1.10.1
Число общеобразовательных учреждений в Белгородской области
(на начало учебного года)
| Год | 2000/ 2001 | 2001/ 2002 | 2002/ 2003 | 2003/ 2004 | 2004/ 2005 |
| Число общеобразовательных учреждений | 823 | 817 | 813 | 807 | 802 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 77
Таблица 1.10.2
Инвестиции в основной капитал, направленные на охрану и рациональное использование земель
| Год | 1999 | 2001 | 2002 | 2003 | 2004 |
| Инвестиции в основной капитал, млн. руб. | 10,8 | 6,3 | 3,9 | 8,7 | 9,0 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 32
Из различного характера интервальных и моментных рядов динамики вытекают некоторые особенности уровней соответствующих рядов.
Уровни интервального ряда динамики абсолютных величин характеризуют собой суммарный итог какого-либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени и поэтому их можно суммировать, как не содержащие повторного счета.
Отдельные же уровни моментного ряда динамики абсолютных величин содержат элементы повторного счета и это делает бессмысленным суммирование уровней рядов динамики.
2) В зависимости от содержания уровней ряды динамики подразделяются на:
§ динамические ряды абсолютных показателей;
§ динамические ряды относительных показателей;
§ динамические ряды средних показателей.
Так, в рассмотренных рядах динамики (табл. 1.10.1 и 1.10.2) уровни выражены абсолютными показателями. Средними показателями могут выражаться уровни, характеризующие динамику средней заработной платы работников предприятия, динамику урожайности винограда и т.д. Относительными показателями характеризуются, например, динамика доли городского и сельского населения (%) и уровня безработицы.
3) В зависимости от расстояния между уровнями, ряды динамики подразделяются на:
§ динамические ряды с равноотстоящими уровнями;
§ динамические ряды с неравноотстоящими уровнями.
Например, ранее приведенные данные о числе общеобразовательных учреждений в Белгородской области за 2000 – 2005 гг. представляют собой ряд динамики с равностоящими уровнями, так как представлены через равные, следующие друг за другом интервалы времени. Если же в рядах даются прерывающиеся периоды или неравномерные интервалы времени, то ряды называются неравноотстоящими (см. пример в таблице 1.10.2).
4) В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на:
§ стационарные ряды динамики;
§ нестационарные ряды динамики.
Важнейшим условием правильного построения ряда динамики являются сопоставимость всех входящих в него уровней; данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.
Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит название смыкания рядов динамики.
Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или в разных территориальных границах. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).
Та же проблема приведения к сопоставимому виду возникает и при параллельном анализе развития во времени экономических показателей отдельных стран, административных и территориальных районов.
Это, во-первых, вопрос о сопоставимости цен сравниваемых стран, во-вторых, вопрос о сопоставимости методики расчета сравниваемых показателей. В таких случаях ряды динамики приводятся к одному основанию, то есть к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.
1.10. 2 Аналитические показатели изменения уровней
ряда динамики
При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики.
Анализ скорости и интенсивности развития явления во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнения уровней между собой. К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процента прироста (см. табл. 1.10.3). При этом принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение - базисным.
Таблица 1.10.3
Аналитические показатели изменения уровней ряда
| № | Название показателя | Цепные | Базисные | Средние |
| 1 | Абсолютный прирост | 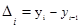
| 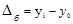
| 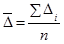 ; ; 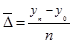
|
| 2 | Темп роста, % | 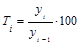
| 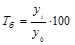
| 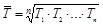 ; ; 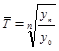
|
| 3 | Темп прироста, % | 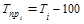
| 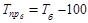
| 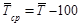
|
| 4 | Абсолютное значение 1-го % прироста |
| ||
Для иллюстрации расчетов статистических показателей, представленных в таблице 1.10.3, рассмотрим динамический ряд производства цемента в экономическом регионе за 1991 – 2002 гг. (табл. 1.10.4.).
Абсолютный прирост ( 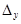 ) -это разность между последующим уровнем ряда и предыдущим (или базисным). Если разность между последующим и предыдущим, то это цепной абсолютный прирост:
) -это разность между последующим уровнем ряда и предыдущим (или базисным). Если разность между последующим и предыдущим, то это цепной абсолютный прирост:
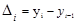 (1.10.1)
(1.10.1)
если между последующим и базисным, то базисный:
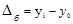 (1.10.2)
(1.10.2)
Подставив значения выпуска цемента из графы 1 (табл. 1.10.4) в формулу (1.10.1), получим абсолютные цепные приросты (графа 2 табл. 1.10.4), в формулу (1.10.2) - базисные приросты (графа 3 табл.1.10.4).
Средний абсолютный прирост исчисляется двумя способами:
1) как средняя арифметическая простая годовых цепных приростов:
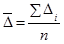 (1.10.3)
(1.10.3)
Подставив в формулу (1.10.3) значения из графы 2 (табл. 1.10.4) в числитель и n=11 (количество сравниваемых лет или число периодов) в знаменатель, получим:
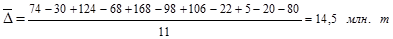
2) как отношение базисного прироста к числу периодов:
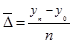 (1.10.4)
(1.10.4)
Подставим в формулу (1.10.4) значения выпуска цемента ( 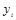 ) из графы 1 табл. 1.10.4, получим:
) из графы 1 табл. 1.10.4, получим:
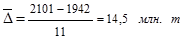
Таблица 1.10.4
Динамика производства продукции предприятия
за 1991-2002 годы
| Год | Продук-ция в сопоста-вимых ценах, млн. т ( | Абсолютные приросты, млн. т | Темпы роста, % | Темпы прироста, % | Абсолют-ное значение 1% прироста, млн. т | |||
| цеп-ные | базис- ные | цеп- ные | базис- ные | цеп- ные | базис- ные | |||
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 | 1942 2016 1986 2110 2042 2210 2112 2218 2196 2201 2181 2101 | - 74 -30 124 -68 168 -98 106 -22 5 -20 -80 | - 74 44 168 100 268 170 276 254 259 239 159 | - 103,8 98,5 106,2 96,8 108,2 95,6 105,0 99,0 100,2 99,1 96,3 | 100,0 103,8 102,3 108,7 105,1 113,8 108,8 114,2 113,1 133,3 112,3 108,2 | - 3,8 -1,5 6,2 -3,2 8,2 -4,4 5,0 -1,0 0,2 -0,9 -3,7 | - 3,8 2,3 8,7 5,1 13,8 8,8 14,2 13,1 33,3 12,3 8,2 | - 19,4 20,2 19,9 21,1 20,4 22,1 21,1 22,2 22,0 22,0 21,8 |
| Итого | 25315 | 159 | - | - | - | - | - | - |
Показатель интенсивности изменения уровня ряда - в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста. Иными словами, коэффициент роста и темп роста представляют собой две формы выражения интенсивности изменения уровня. Однако необходимо отметить, что ненужно пользоваться одновременно двумя формами, которые по существу идентичны. Разница между ними заключается только в единице измерения. Он бывает цепным и базисным.
Цепной темп роста - это отношение последующего уровня к предыдущему, умноженному на 100%, если исчисление идет в процентах, как в нашем случае:
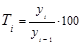 (1.10.5)
(1.10.5)
Подставив в формулу (1.10.5) соответствующие данные графы 1 табл. 1.10.4, получим значения цепного темпа роста, см. графу 4 табл. 1.10.4.
Базисный темп роста - это отношение каждого последующего уровня к одному уровню, принятому за базу сравнения:
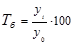 (1.10.6)
(1.10.6)
Подставив в формулу (1.10.6) те же данные, что и в предыдущую, получим значения базисного темпа роста, см. графу 5 табл.1.10.4.
Следует отметить, что между цепными и базисными темпами роста есть взаимосвязь. Зная базисные темпы, можно исчислить цепные делением каждого последующего базисного темпа на предыдущий.
Средний темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
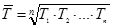 (1.10.7)
(1.10.7)
Для этого показатели графы 4, выраженные в процентах, переведем в коэффициенты, подставив в формулу (1.10.7), получим:
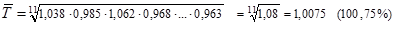
Средний темп роста может быть исчислен вторым способом, исходя из конечного и начального уровней по формуле:
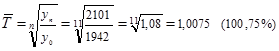
Из этого расчета можно сделать вывод, что среднегодовой темп роста составил за 1991-2002 г. - 100,75%.
Наряду с темпом роста можно рассчитать показатель темпа прироста, характеризующий относительную скорость изменения уровня ряда в единицу времени. Темп прироста показывает, на какую долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня.
Темп прироста есть отношение абсолютного прироста к уровню ряда, принятого за базу. Темп прироста – величина положительная, если сравниваемый уровень больше базисного, и наоборот.
Определяется как разность между темпами роста и 100% , если темпы роста выражены в процентах:
цепной - 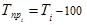 (1.10.8)
(1.10.8)
базисный - 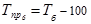 (1.10.9)
(1.10.9)
Для определения темпа прироста цепного берем разность между темпом роста цепным (графа 4 табл. 1.10.4) и ста процентами, для базисного - между темпом роста базисным (графа 5 табл. 1.10.4) и ста процентами.
Подставив все соответствующие данные в формулы (1.10.8 и 1.10.9), получим значения темпов прироста цепных (графа 6 табл. 1.10.4) и базисных (графа 7 табл. 1.10.4).
Среднегодовой темп прироста исчисляется подобно темпу прироста по формуле:
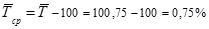
Таким образом, производство цемента за исследуемые годы увеличивалось в среднем за год на 0,75%.
В статистической практике часто вместо расчета и анализа темпов роста и прироста рассматривают абсолютное значение одного процента прироста. Оно представляет собой одну сотую часть базисного уровня и в то же время - отношение абсолютного прироста к соответствующему темпу прироста:
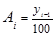 (1.10.10)
(1.10.10)
Подставив данные графы 1 за предыдущий год, деленные на 100% (1942:100=19,4) в формулу (1.10.10), получим абсолютное значение 1% прироста (см. графу 8 табл. 1.10.4).
Средний уровень ряда динамики ( 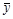 ) рассчитывается по средней хронологической. Средней хронологической называется средняя, исчисленная из значений, изменяющихся во времени. Такие средние обобщают хронологическую вариацию. В хронологической средней отражается совокупность тех условий, в которых развивалось изучаемое явление в данном промежутке времени.
) рассчитывается по средней хронологической. Средней хронологической называется средняя, исчисленная из значений, изменяющихся во времени. Такие средние обобщают хронологическую вариацию. В хронологической средней отражается совокупность тех условий, в которых развивалось изучаемое явление в данном промежутке времени.
Методы расчета среднего уровня интервального и моментного рядов динамики различны. Для интервальных равноотстоящих рядов средний уровень находится по формуле средней арифметической простой и для неравноотстоящих рядов по средней арифметической взвешенной:
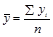 (1.10.11)
(1.10.11)
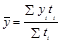 (1.10.11)
(1.10.11)
где 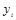 - уровень ряда динамики;
- уровень ряда динамики;
n - число уровней;
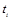 - длительность интервала времени между уровнями.
- длительность интервала времени между уровнями.
Так, в таблице 1.10.4 приведен интервальный ряд динамики с равноотстоящими уровнями. По этим данным можно рассчитать среднегодовой уровень производства цемента за 1991-2002 гг. Он будет равен:
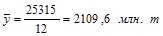
Средний уровень моментного ряда динамики так исчислить нельзя, так как отдельные уровни содержат элементы повторного счета.
Средний уровень моментного равноотстоящего ряда динамики находится по формуле средней хронологической:
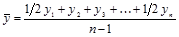 (1.10.12)
(1.10.12)
Например, если известны товарные остатки магазина на 1-ое число каждого месяца (тыс. руб.):
1/I 1/II 1/III 1/IV
28 23 27 31
то среднемесячный товарный остаток за 1 квартал по формуле (1.10.12) составит:
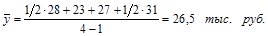
Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной:
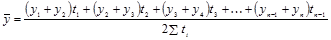 (1.10.13)
(1.10.13)
где 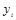 ,
, 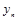 - уровни ряда динамики;
- уровни ряда динамики;
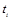 - длительность интервала времени между уровнями.
- длительность интервала времени между уровнями.
Например, численность населения города составляла в 2002 г.: по состоянию на 1 января – 1238 тыс. чел.; на 1 марта – 1240 тыс. чел.; на 1 июня – 1350 тыс. чел.; на 1 ноября – 1370 тыс. чел.; на 1 января 2003 г. – 1420 тыс. чел.
Средняя численность населения города (тыс. чел.) в 2002 г. по формуле (1.10.13) составит:
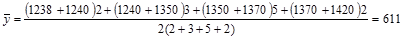
1.10.3 Методы выравнивания рядов динамики
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития, присущей тому или иному ряду динамики. Например, за колебаниями урожайности какой-либо сельскохозяйственной культуры в отдельные годы тенденция роста (уменьшения) урожайности может не просматриваться непосредственно, и поэтому должна быть выявлена статистическими методами.
Методы анализа основной тенденции в рядах динамики разделяются на две основные группы:
1) сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней;
2) выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, присущую ряду и одновременно освободила его от незначительных колебаний.
Рассмотрим методы каждой группы.
Метод укрупнения интервалов. Если рассматривать уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдается снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. В этом случае для наглядного представления тренда применяется метод укрупнения интервалов, который основан на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д.
Метод простой скользящей средней. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней, начиная со второго, далее - начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень вначале и добавляя один следующий. Отсюда название - скользящая средняя.
Расчет скользящей средней по данным об урожайности зерновых культур приведен в таблице 1.10.5.
Сглаженный ряд урожайности по трехлетиям короче фактического на один член ряда в начале и в конце, по пятилетиям – на два в начале и в конце ряда. Он меньше, чем фактический подвержен колебаниям из-за случайных причин, и четче выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.
Таблица 1.10.5
Сглаживание урожайности зерновых культур
методом скользящей средней
| Фактический уровень урожайности, ц/га | Скользящая средняя | |
| трехлетняя | пятилетняя | |
| 15,4 14,0 17,6 15,4 10,9 17,5 15,0 18,5 14,2 14,9 | - (15,4+14,0+17,6)/3=15,7 (14,0+17,6+15,4)/3=15,7 (17,6+15,4+10,9)/3=14,6 (15,4+10,9+17,5)/3=14,6 (10,9+17,5+15,0)/3=14,5 (17,5+15,0+18,5)/3=17,0 (15,0+18,5+14,2)/3=15,9 (18,5+14,2+14,9)/3=15,9 - | - - (15,4+14,0+17,6+15,4+10,9)/5=14,7 (14,0+17,6+15,4+10,9+17,5)/5=15,1 (17,6+15,4+10,9+17,5+15,0)/5=15,2 (15,4+10,9+17,5+15,0+18,5)/5=17,1 (10,9+17,5+15,0+18,5+14,2)/5=16,8 (17,5+15,0+18,5+14,2+14,9)/5=17,6 - - |
Недостаток метода простой скользящей средней состоит в том, что сглаженный ряд динамики сокращается ввиду невозможности получить сглаженные уровни для начала и конца ряда. Этот недостаток устраняется применением метода аналитического выравнивания для анализа основной тенденции.
Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени - y 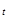 =f(t).
=f(t).
Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы степени, экспоненты, логистические кривые и другие виды. Полиномы имеют следующий вид:
полином первой степени: 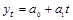
полином второй степени: 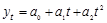
полином третьей степени: 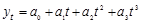
полином n-ой степени: 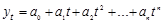
Здесь 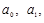
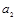 ,...
,... 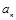 - параметры полиномов, t - условное обозначение времени. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр
- параметры полиномов, t - условное обозначение времени. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр 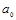 трактуется как характеристика средних условий ряда динамики, параметры
трактуется как характеристика средних условий ряда динамики, параметры 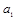 ,
, 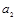 ,
, 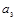 - как изменения ускорения.
- как изменения ускорения.
В статистике выработано правило выбора степени полинома модели развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу полином первой степени (прямая) применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) постоянны, полиномы второй степени - для отражения ряда динамики с постоянными вторыми разностями (ускорениями), полиномы третьей степени - с постоянными третьими разностями и т.д.
Рассмотрим «технику» выравнивания ряда динамики по прямой (полином первой степени): 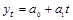 . Параметры
. Параметры 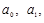 согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений:
согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений:
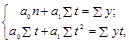 (1.10.14)
(1.10.14)
где у – фактические (эмпирические) уровни ряда;
t – время (порядковый номер периода или момента времени).
Расчет параметров значительно упрощается, если за начало отсчета времени (t=0) принять центральный интервал (момент).
При четном числе уровней значения t – условного обозначения времени будут такими:
…-5, -3, -1, +1, +3, +5,…
При нечетном числе уровней значения устанавливаются по-другому:
…-3, -2, -1, 0, +1, +2, +3, …
В обоих случаях 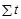 =0, так что система нормальных уравнений (1.10.14) принимает вид:
=0, так что система нормальных уравнений (1.10.14) принимает вид:
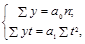 (1.10.15)
(1.10.15)
Из первого уравнения 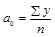 (1.10.16),
(1.10.16),
из второго - 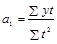 (1.10.17).
(1.10.17).
Проиллюстрируем на примере динамического ряда производства цемента в экономическом регионе за 1991 – 2002 гг. (см. табл. 1.10.4, расчетные значения – табл. 1.10.6) выравнивание ряда динамики по прямой. Для выравнивания данного ряда используем линейную трендовую модель – уравнение прямой: 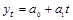 . В нашем примере n = 12 – четное число. Для упрощения расчетов обозначим время так, чтобы начало его отсчета приходилось на середину рассматриваемого периода.
. В нашем примере n = 12 – четное число. Для упрощения расчетов обозначим время так, чтобы начало его отсчета приходилось на середину рассматриваемого периода.
Таблица 1.10.6
Выравнивание по прямой ряда динамики
производства цемента
| Годы | Производство цемента, млн. т
( 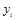 ) )
| t | 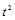
| 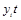
| 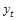
| 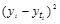
|
| А | 1 | 2 | 3 | 4 | 5 | 6 |
| 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 | 1942 2016 1986 2110 2042 2210 2112 2218 2196 2201 2181 2101 | -11 -9 -7 -5 -3 -1 1 3 5 7 9 11 | 121 81 49 25 9 1 1 9 25 49 81 121 | -21362 -18144 -13902 -10550 -6126 -2210 2112 6654 10980 15407 19629 23111 | 2002,02 2021,58 2041,14 2060,7 2080,26 2099,82 2119,38 2138,94 2158,5 2178,06 2197,62 2217,18 | 3602,4004 31,1364 3040,4196 2430,49 1463,8276 12139,6324 54,4644 6250,4836 1406,25 526,2436 276,2244 13497,7924 |
| Сумма | 25315 | 0 | 572 | 5599 | 25315 | 44719,3648 |
Параметры 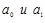 искомого уравнения прямой исчислим по формулам (1.10.16) и (1.10.17).
искомого уравнения прямой исчислим по формулам (1.10.16) и (1.10.17).
Из таблицы 1.10.6 находим: 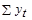 = 25315;
= 25315; 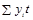 = 5599;
= 5599; 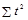 = 572,
= 572,
Откуда 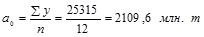 ;
;
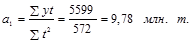
Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид:
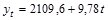
Подставив в полученное уравнение прямой значения t из графы 2 табл. 1.10.6, получим теоретические уровни (см. графу 5 табл. 1.10.6).
Если расчеты выполнены правильно, то 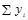 =
= 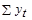 . В нашем примере
. В нашем примере 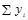 =
= 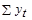 = 25315. Следовательно, значения уровней выравненного ряда найдены верно.
= 25315. Следовательно, значения уровней выравненного ряда найдены верно.
Полученное уравнение показывает что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения производства цемента: с 1991 по 2002 гг. производство цемента в среднем возрастало на 9,78 млн. т в год.
Фактические и расчетные значения производства цемента представлены в виде графика (см. рис. 1.10.1).
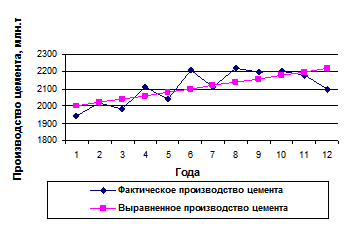
Рис. 1.10.1 Фактические и выравненные годовые уровни
производства цемента
Соединив точки, построенные по фактическим данным, получим ломаную линию, на основании которой затруднительно вынести суждение о характере общей тенденции в изменении производства цемента. Тенденция роста производства цемента в изучаемом периоде отчетливо проявляется в результате построения выравненной прямой 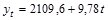 .
.
1.10.4 Методы выявления сезонной компоненты
При рассмотрении квартальных или месячных данных многих социально-экономических явлений часто обнаруживаются определенные, постоянно повторяющиеся колебания, которые существенно не изменяются за длительный период времени. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также ряда многочисленных разнообразных факторов, которые частично являются регулируемыми. В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезонных колебаний» или «сезонных волн», а динамический ряд в этом случае называют тренд-сезонным, или просто сезонным рядом динамики.
Сезонные колебания характеризуются специальным показателями, которые называются индексами сезонности ( 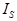 ). Совокупность этих показателей отражает сезонную волну. Индексами сезонности являются процентные отношения фактических внутригодовых уровней к постоянной или переменной средней.
). Совокупность этих показателей отражает сезонную волну. Индексами сезонности являются процентные отношения фактических внутригодовых уровней к постоянной или переменной средней.
Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам. Данные за несколько лет (обычно не менее трех) берутся для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года.
Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным без их предварительного выравнивания.
Для каждого месяца рассчитывается средняя величина уровня, например, за три года ( 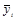 ), затем из них рассчитывается среднемесячный уровень для всего ряда (
), затем из них рассчитывается среднемесячный уровень для всего ряда ( 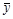 ) и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, то есть:
) и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, то есть:
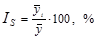 (1.10.18)
(1.10.18)
Если же ряд динамики содержит определенную тенденцию в развитии, то прежде чем вычислить сезонную волну, фактические данные должны быть обработаны так, чтобы была выявлена общая тенденция.
Обычно для этого прибегают к аналитическому выравниванию ряда динамики.
При использовании способа аналитического выравнивания ход вычислений индексов сезонности следующий:
§ по соответствующему полиному вычисляются для каждого месяца (квартала) выровненные уровни на момент времени (t);
§ вычисляются отношения фактических месячных (квартальных) данных ( 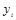 ) к соответствующим выровненным данным (
) к соответствующим выровненным данным ( 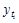 ):
): 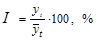 ;
;
§ находятся средние арифметические из процентных соотношений, рассчитанных по одноименным периодам в процентах 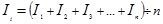 , где n – число одноименных периодов.
, где n – число одноименных периодов.
В общем виде формулу расчета индекса сезонности данным способом можно записать так:
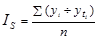 (1.10.19)
(1.10.19)
Расчет заканчивается проверкой правильности вычислений индексов, так как средний индекс сезонности для всех месяцев (кварталов) должен быть 100 процентов, то сумма полученных индексов по месячным данным равна 1200, а сумма по четырем кварталам - 400.
1.10.5 Элементы прогнозирования. Интерполяция и
экстраполяция в рядах динамики
Необходимым условием регулирования рыночных отношений является составление надежных прогнозов развития социально–экономических явлений.
Важное место в системе методов прогнозирования занимают статистические методы. Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохранится и в прогнозируемом будущем, то есть прогноз основан на экстраполяции. Экстраполяция, проводимая в будущее, называется перспективой и в прошлое - ретроспективой. Обычно, говоря об экстраполяции рядов динамики, подразумевает чаще всего перспективную экстраполяцию.
Применение экстраполяции в прогнозировании базируется на следующих предпосылках:
§ развитие исследуемого явления в целом описывается плавной кривой;
§ общая тенденция развития явления в прошлом и настоящем не претерпет серьезных изменений в будущем.
Поэтому надежность и точность прогноза зависят от того, насколько близкими к действительности окажутся эти предположения, а также как точно удастся охарактеризовать выявленную в прошлом закономерность. Экстраполяцию следует рассматривать как начальную стадию построения окончательных прогнозов.
В зависимости от того, какие принципы и какие исходные данные положены в основу прогноза, можно выделить следующие элементарные методы экстраполяции: среднего абсолютного прироста, среднего темпа роста и экстраполяция на основе выравнивания рядов по какой-либо аналитической формуле.
Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной, то есть метод основан на предположении о равномерном изменении уровня (под равномерностью понимается стабильность абсолютных приростов).
Для нахождения интересующего нас аналитического выражения тенденции на любую дату t необходимо определить средний абсолютный прирост и последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов, экстраполируется ряд, то есть экстраполяцию можно сделать по следующей формуле:
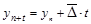 (1.10.20)
(1.10.20)
где 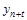 - экстраполируемый уровень, (n +t) - номер этого уровня (года);
- экстраполируемый уровень, (n +t) - номер этого уровня (года);
n - номер последнего уровня (года) исследуемого периода, за который рассчитан 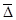 ;
;
t - срок прогноза (период упреждения);
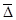 - средний абсолютный прирост.
- средний абсолютный прирост.
Так, по данным табл. 1.10.6, на основе исчисленного ранее уравнения 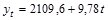 , экстраполяцией при t=13 можно определить ожидаемое производство цемента в 2003 г., млн. т:
, экстраполяцией при t=13 можно определить ожидаемое производство цемента в 2003 г., млн. т:
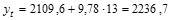
Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. Для нахождения тенденции в этом случае необходимо определить средний коэффициент роста, возведенный в степень, соответствующую периоду экстраполяции, то есть по формуле:
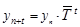 (1.10.21)
(1.10.21)
где 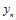 - последний уровень ряда динамики;
- последний уровень ряда динамики;
t - срок прогноза;
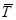 - средний коэффициент роста.
- средний коэффициент роста.
Если же ряду динамики свойственна иная закономерность, то данные, полученные при экстраполяции на основе среднего темпа роста, будут отличаться от данных, полученных другими способами экстраполяции.
Рассмотренные способы экстраполяции тренда, будучи простейшими, в то же время являются и самыми приближенными.
Поэтому наиболее распространенным методом прогнозирования является аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t).
При таком подходе к прогнозированию предполагается, что размер уровня, характеризирующего явление, формируется под воздействием множества факторов, причем не представляется возможным выделить отдельно их влияние. В связи с этим, ход развития связывается не с какими-либо конкретными факторами, а с течением времени, то есть y=f(t). Поэтому целесообразно определение доверительных интервалов прогноза. Величина доверительного интервала определяется следующим образом:
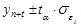 (1.10.22)
(1.10.22)
где 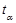 - коэффициент доверия по распределению Стьюдента;
- коэффициент доверия по распределению Стьюдента;
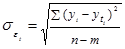 - остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (n-m);
- остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (n-m);
n - число уровней ряда динамики;
m - число параметров адекватной модели тренда (для уравнения прямой m=2).
Рассчитаем прогнозируемые доверительные интервалы производства цемента на 2003 г.
Если n=12 и m=2, то число степеней свободы равно 10. Тогда при доверительной вероятности, равной 0,95 (то есть при уровне значимости случайностей 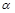 =0,5), коэффициент доверия
=0,5), коэффициент доверия 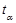 =2,306 (по таблице Стьюдента),
=2,306 (по таблице Стьюдента), 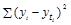 =44719,3648 (см. табл. 1.10.6).
=44719,3648 (см. табл. 1.10.6).
Тогда 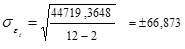 .
.
Зная точечную оценку прогнозируемого значения производства цемента 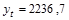 млн. т, определяем вероятностные границы интервала:
млн. т, определяем вероятностные границы интервала:
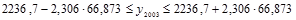 , отсюда
, отсюда
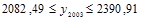 .
.
Следовательно, с вероятностью 0,95, можно утверждать, что производство цемента в 2003 г. не менее чем 2082,49, но и не более чем 2390,91 млн. т.
При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, то есть к интерполяции.
Как и экстраполяция, интерполяция может производиться на основе среднего абсолютного прироста, среднего темпа роста, а также с помощью аналитического выравнивания.
Интерполяция также основана на том или ином предположении о тенденции изменения уровней, но здесь уже не приходится предполагать, что тенденция, характерная для прошлого, сохранится и в будущем. При интерполяции предполагается, что ни выявленная тенденция, ни ее характер не претерпели существенных изменений в том промежутке времени, уровень (уровни) которого нам неизвестны.
Тренировочные задания
1. Имеются следующие данные о производстве стали в России:
| Годы | 2000 | 2001 | 2002 | 2003 | 2004 |
| Производство стали, млн. тонн | 59,1 | 59,0 | 58,0 | 61,3 | 64,1 |
// «РЦБ» №12 (291), 2005
Определите цепные и базисные:
а) абсолютные приросты;
б) темпы роста;
в) темпы прироста.
Решение:
а) величина абсолютного прироста – это разность двух сравниваемых величин.
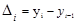 или
или 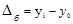 ,
,
где 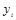 – уровень i-го года,
– уровень i-го года,
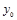 – уровень базисного года.
– уровень базисного года.
| Годы | 2000 | 2001 | 2002 | 2003 | 2004 | |
| Абсолютный прирост, млн. тонн | к предыдущему году | - | -0,1 | -1,0 | 3,3 | 2,8 |
| к базисному 2000 году | - | -0,1 | -1,1 | 2,2 | 5,0 |
б) Интенсивность изменения уровней ряда динамики оцениваются отношением текущего уровня к предыдущему или базисному, которое всегда представляет собой положительное число. Поэтому темпы роста представим в следующей таблице:
| Годы | 2000 | 2001 | 2002 | 2003 | 2004 | |
| Темп роста, % | к предыдущему году | - | 99,8 | 98,3 | 105,7 | 104,6 |
| к базисному 2000 году | 100 | 99,8 | 98,1 | 103,7 | 108,5 |
в) для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяем темп прироста, который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, или 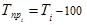 - цепной и
- цепной и 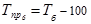 - базисный:
- базисный:
| Годы | 2000 | 2001 | 2002 | 2003 | 2004 | |
| Темпы прироста, % | к предыдущему году | - | -0,2 | -1,7 | 5,7 | 4,6 |
| к базисному 2000 году | - | -0,2 | -1,9 | 3,7 | 8,5 |
2. Закупка картофеля организациями потребительской кооперации региона за три года составила:
| Месяцы | Годы | ||
| 1 год | 2 год | 3 год | |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | 168 212 234 636 761 868 535 164 1217 925 416 346 | 243 317 329 606 910 1032 515 244 860 1240 354 175 | 205 184 269 572 702 801 290 443 207 2308 331 389 |
Измерьте сезонные колебания реализации картофеля, исчислив индексы сезонности. Сделайте выводы.
Решение:
Возьмем данные по условию, занесем их в графы 1-4 табл. 1.10.7 и проведем расчет индексов сезонности.
По данным таблицы 1.10.7 вычислим усредненные значения уровней по одноименным периодам способом арифметической простой:
январь: 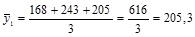 ;
;
февраль: 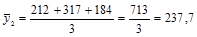 и т.д. (графа 5 табл. 1.10.7).
и т.д. (графа 5 табл. 1.10.7).
Затем по вычисленным помесячным средним уровням (  ) определим общий средний уровень (
) определим общий средний уровень (  ):
):
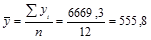
или
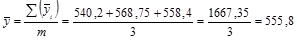
где m - число лет;
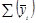 - сумма среднегодовых уровней ряда динамики.
- сумма среднегодовых уровней ряда динамики.
Таблица 1.10.7
Динамика реализации картофеля организациями
потребительской кооперации региона
| Месяцы | Годы | Индекс сезонности
| |||
1 год
| 2 год
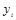
| 3 год
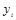
| в среднем
за три года
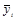
| ||
| 1 | 2 | 3 | 4 | 5 | 6 |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | 168 212 234 636 761 868 535 164 1217 925 416 346 | 243 317 329 606 910 1032 515 244 860 1240 354 175 | 205 184 269 572 702 801 290 443 207 2308 331 389 | 205,3 237,7 277,3 604,7 791,0 900,3 446,7 283,7 761,3 1491,0 367,0 303,3 | 36,9 42,8 49,9 108,8 142,3 162,0 80,4 51,0 137,0 268,3 66,0 54,6 |
Средний уровень ряда
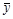
| 540,2 | 568,75 | 558,4 | 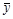 = 555,8 = 555,8
| 100,0 |
Далее рассчитаем по месяцам года индексы сезонности:
январь: 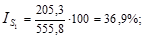
февраль: 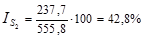 и т.д. (графа 6 табл. 1.10.7)
и т.д. (графа 6 табл. 1.10.7)
Совокупность исчисленных индексов сезонности характеризует сезонную волну реализации картофеля.
Анализ данных табл. 1.10.7 позволяет сделать следующие выводы:
1) реализация картофеля характеризуется резко выраженной сезонностью;
2) закупка картофеля по отдельным месяцам года отклоняется от среднемесячной закупки на 62 – 168%;
3) наименьшей реализацией картофеля характеризуется январь (36,9%), а наибольшей – октябрь (268,3%).
3. Имеются основные показатели деятельности аспирантуры:
| Годы | Численность аспирантов (на конец года), чел. |
| 1999 | 479 |
| 2000 | 560 |
| 2001 | 619 |
| 2002 | 740 |
| 2003 | 827 |
| 2004 | 918 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 182
Для анализа ряда динамики:
1) определите цепные и базисные: абсолютные приросты; темпы роста; темпы прироста;
2) определите для каждого года абсолютное значение 1% прироста;
3) рассчитайте среднегодовой абсолютный прирост, темп роста, темп прироста;
4) рассчитайте прогноз на 2005 и 2006 годы;
5) проведите аналитическое выравнивание динамического ряда.
Результаты расчетов оформите в таблице.
4. Динамика индекса потребительских цен РФ характеризуется следующими данными:
| Годы | ИПЦ РФ, раз |
| 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 | 2,6 26,1 9,4 3,2 2,3 1,2 1,1 1,8 1,4 1,2 1,2 1,2 1,1 |
Рассчитать изменение цен в 2003 году по отношению к 1991 (цепной метод).
5. Имеются следующие данные о развитии инфраструктуры сельской местности в Белгородской области:
| Годы | 1999 | 2000 | 2001 | 2002 | 2003 |
| Ввод в действие газовых сетей, км | 916,9 | 451,4 | 118,2 | 117,8 | 212,7 |
// Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 129
Рассчитайте индексы цепных и базисных: абсолютных приростов и темпов роста. Результаты изложите в таблице.
6. Имеются следующие данные о товарных запасах в розничной торговле за первый квартал, тыс. руб.:
| Товарные группы | на 1/I | на 1/II | на 1/III | на 1/IV |
| Продовольственные товары | 1620 | 1720 | 1380 | 1540 |
| Непродовольственные товары | 2800 | 2690 | 2809 | 2750 |
Определите средние товарные запасы за первый квартал по каждой товарной группе и в целом по двум группам.
7. Динамика кредитных ресурсов коммерческого банка на начало месяца характеризуется данными:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Кредитные ресурсы, млн. руб. | 48 | 53 | 51 | 50 | 55 | 52 | 54 |
Определите средний объем кредитных ресурсов за первый и второй квартал, абсолютный прирост и темп прироста среднего объема.
8. Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным об объеме промышленной продукции по области:
| Годы | Объем промышленной продукции, млн. руб. | По сравнению с предыдущим годом | |||
| Абсолютный прирост, млн. руб. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн. руб. | ||
| 1998 1999 2000 2001 2002 2003 | 32500,5 | 6249,8 5898,6 | 106,9 | 23,0 | 616,033 |
9. Среднесуточное потребление электроэнергии характеризуется следующими данными, тыс. кВт-ч:
| Январь Февраль Март Апрель Май Июнь | 16,7 14,1 13,4 9,7 8,2 7,5 | Июль Август Сентябрь Октябрь Ноябрь Декабрь | 8,4 9,8 10,9 12,2 15,8 17,3 |
Определите индексы сезонности на основе постоянной средней, вычислите амплитуду колебаний.
Опишите сезонную волну графически.
10. Имеются следующие данные о среднем размере товарных запасов в супермаркете по месяцам года:
| Месяцы | Средний размер товарных запасов, млн. руб. |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | 99,6 100,1 99,6 100,1 99,6 98,7 98,7 94,9 90,2 94,5 97,8 99,2 |
Произведите:
а) сглаживание ряда товарных запасов супермаркета методом четырёхчленной скользящей средней;
б) выравнивания ряда динамики по прямой.
Сделайте выводы о характере общей тенденции изучаемого явления.
11. Динамика урожайности плодово-ягодных культур и виноградников в области характеризуется следующими данными:
| Годы | Урожайность, ц/га | |
| плодов и ягод | винограда | |
| 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 | 47,1 38,1 32,3 40,9 50,5 30,1 39,4 44,2 39,2 35,5 41,6 42,3 44,5 | 54,2 57,4 49,2 34,0 61,6 53,4 59,8 61,9 59,4 50,8 58,2 58,6 59,5 |
Проведите сглаживание рядов динамики методом трехчленной скользящей средней.
Сделайте выводы относительно тенденции урожайности.
Тест
1. Ряд динамики характеризует:
а) изменение характеристики совокупности в пространстве;
б) изменение характеристики во времени;
в) структуру совокупности по какому-либо признаку.
2. Базисный абсолютный прирост равен:
а) сумме цепных абсолютных приростов;
б) произведению цепных абсолютных приростов;
в) сумме цепных темпов роста;
г) произведению цепных темпов роста.
3. Темп роста вычисляется как:
а) произведение уровней ряда;
б) сумма уровней ряда;
в) отношение уровней ряда;
г) разность уровней ряда.
4. Средний прирост используется для вычисления прогнозного значения в следующей точке, если:
а) цепные абсолютные приросты примерно одинаковы;
б) цепные темпы роста примерно одинаковы;
в) базисные абсолютные приросты примерно одинаковы.
5. Средний темп роста рассчитывается по формуле:
а) средней арифметической;
б) средней гармонической;
в) средней геометрической.
6. Средний уровень интервального ряда динамики определяется как:
а) средняя арифметическая;
б) средняя хронологическая;
в) средняя гармоническая.
7. Определите средний годовой темп прироста за 2001-2003 гг., если темпы роста выпуска изделия «А» в отрасли составили: в 2001 г. - 103%, в 2002 г. – 102%, в 2003 г. – 105%.
а) 3,5%;
б) 5,0%;
в) 5,2%;
г) 3,3%.
8. При сглаживании временного ряда с помощью 5-членной скользящей средней теряются:
а) только первые два значения временного ряда;
б) только последние два значения временного ряда;
в) два первых и два последних значения временного ряда;
г) пять первых и пять последних значений временного ряда.
9. На участке №1 средняя часовая выработка увеличилась за 2 года на 30%, на участке №2 трудоёмкость снизилась на 2,5%. На каком участке выше темп прироста производительности труда?
а) на первом;
б) на втором;
в) одинаковый.
10. Вычислите средний уровень моментного ряда динамики, если известны товарные остатки магазина на 1-ое число каждого месяца (млн. руб.):
на 1 января - 20;
на 1 февраля - 18;
на 1 марта - 16;
на 1 апреля - 15.
а) 16,8;
б) 16,3;
в) 17,17;
г) 17,25.
11. Каковы должны быть в среднем ежегодные темпы прироста, чтобы продукция за три года возросла с 60 до 70 млн. руб.?
а) 5,3%;
б) 3,3%;
в) 6,0%;
г) 5,0%.
12. В 2000 г. инвестиции в отрасль составляли 200 млн. ден. ед. За 2001 г. объем инвестиций увеличился на 36, а за 2002 г. – на 52 млн. ден. ед. Определите среднегодовой темп прироста инвестиций за 2001 – 2002 гг.
а) 22;
б) 10;
в) 44;
г) 20.
13. По состоянию на 1 января отчётного года в штате фирмы состояло 130 человек. 14 января было принято 5 новых сотрудников, 19 января уволено 3 человека, 28 января уволено 6 человек. Определите среднюю численность работников фирмы за январь.
а) 128,0;
б) 132;
в) 126;
г) 130,9.
14. Назовите методы сглаживания рядов динамики:
а) метод наименьших квадратов;
б) метод скользящей средней;
в) метод укрупнения интервалов.
15. В линейном уравнении тренда 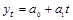 параметр
параметр 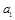 характеризует:
характеризует:
а) среднегодовой темп изменения (в разах);
б) среднегодовой абсолютный прирост;
в) среднегодовой темп прироста.
16. Остатки нереализованной готовой продукции на складе фирмы на начало каждого квартала – это ряд динамики:
а) моментный;
б) интервальный.
17. В 2002 г. выручка от продаж продукции (работ, услуг) фирмы увеличилась по сравнению с прошлым годом на 20%, абсолютное значение 1% прироста – 15 тыс. руб. Определите выручку от продаж продукции (работ, услуг) фирмы в 2002 г.:
а) 18 тыс. руб.;
б) 35 тыс. руб.;
в) 1,8 млн. руб.;
г) 1,25 млн. руб.
18. Потребление электроэнергии в регионе в прошлом году выросло в 1,12 раза, в текущем - на 35%. Определите темп роста потребления электроэнергии за два года.
а) 147%;
б) 39,2%;
в) 151,2%;
г) 148,5%.
19. На основе годовых данных об изменении урожайности плодово-ягодных культур в регионе были оценены коэффициенты линейного тренда: 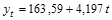 . В соответствии с этой моделью среднегодовой прирост урожайности составляет:
. В соответствии с этой моделью среднегодовой прирост урожайности составляет:
а) 163,59 ц/га;
б) 4,197 ц/га;
в) (163,59+4,197) ц/га;
г) 4,197%.
20. Можно ли изучить взаимосвязи социально-экономических явлений по данным рядов динамики:
а) да;
б) нет.