При построении моделей регрессии должны соблюдаться
следующие требования:
1. Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.
2. Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей.
3. Все факторные признаки должны иметь количественное (цифровое) выражение.
4. Наличие достаточно большого объема исследуемой выборочной совокупности.
5. Причинно-следственные связи между явлениями и процессами должны описываться линейной или приводимой к линейной форме зависимостью.
6. Отсутствие количественных ограничений на параметры модели связи.
7. Постоянство территориальной и временной структуры изучаемой совокупности.
Соблюдение данных требований позволяет построить модель, наилучшим образом описывающую реальные явления и процессы.
1.9.2 Парная регрессия на основе метода наименьших
квадратов и метода группировок
Парная регрессия характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями:
прямой 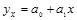
гиперболы 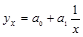
параболы 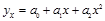 (1.9.3)
(1.9.3)
показательной функции 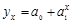
полулогарифметической функции 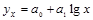 и так далее.
и так далее.
Определить тип уравнения можно, исследуя зависимость графически, однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи - гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия.
Оценка параметров уравнений регрессии ( 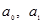 и
и 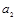 - в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели (
- в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели ( 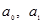 ), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
), при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
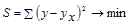 (1.9.4)
(1.9.4)
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
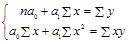 (1.9.5)
(1.9.5)
где n - объем исследуемой совокупности (число единиц наблюдения).
В уравнениях регрессии параметр a 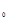 показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков; коэффициент регрессии a
показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков; коэффициент регрессии a 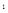 показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.
Пример. По данным наблюдения окупаемость затрат на радиоприборы зависит от срока освоения их производства (см. табл. 1.9.2).
Таблица 1.9.2
Зависимость между окупаемостью затрат и сроком освоения
производства приборов
| № продук- ции | Срок освоения, лет (x) | Окупаемость затрат, тыс. ден. ед. (y) | 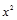
| 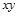
| 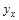
|
| 1 2 3 4 5 6 7 8 9 10 | 5 4 7 10 1 2 8 12 3 6 | 10,2 7,5 13,9 12,8 0,6 2,8 13,2 10,1 5,4 12,7 | 25 16 49 100 1 4 64 144 9 36 | 51 30 97,3 128 0,6 5,6 105,6 121,2 16,2 76,2 | 8,104 7,084 10,144 13,204 4,024 5,044 11,164 15,244 6,064 9,124 |
| Итого | 58 | 89,2 | 448 | 631,7 | 89,2 |
Предположим наличие линейной зависимости между рассматриваемыми признаками. Тогда, система нормальных уравнений для данного примера будет иметь следующий вид:
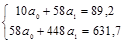
Отсюда: a 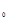 = 3,004; a
= 3,004; a 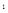 = 1,02. Следовательно,
= 1,02. Следовательно, 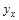 =3,004 + 1,02x.
=3,004 + 1,02x.
На практике исследования часто проводятся по большому числу наблюдений. В этом случае исходные данные удобнее представлять в сводной групповой таблице. При этом анализу подвергаются сгруппированные данные и по факторному (x) и по результативному (y) признакам, то есть уравнения парной регрессии целесообразно строить на основе сгруппированных данных.
1.9.3 Множественная (многофакторная) регрессия
Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии:
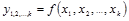 (1.9.6)
(1.9.6)
Построение моделей множественной регрессии включает несколько этапов:
1. Выбор формы связи (уравнения регрессии);
2. Отбор факторных признаков;
3. Обеспечение достаточного объема совокупности.
Выбор типа уравнения затрудняется тем, что для любой формы зависимости можно выбрать целый ряд уравнений, которые в определенной степени будут описывать эти связи. Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации.
Важным этапом построения уже выбранного уравнения множественной регрессии является отбор и последующее включение факторных признаков.
С одной стороны, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью 100 и более факторных признаков сложно реализуема и требует больших затрат машинного времени. Сокращение размерности модели за счет исключения второстепенных, экономически и статистически несущественных факторов способствует простоте и качеству ее реализации. В то же время построение модели регрессии малой размерности может привести к тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам.
Проблема отбора факторных признаков для построения моделей взаимосвязи может быть решена на основе интуитивно-логических или многомерных статистических методов анализа.
Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность метода шаговой регрессии заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Факторы поочередно вводятся в уравнение так называемым «прямым методом». При проверке значимости введенного фактора определяется на сколько уменьшается сумма квадратов остатков и увеличивается величина множественного коэффициента корреляции (R 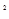 ). Одновременно используется и обратный метод, то есть исключение факторов, ставших незначимыми. Фактор является незначимым, если его включение в уравнение регрессии только изменяет значения коэффициентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения. Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициента регрессии не изменяется (или меняется несущественно), то данный признак существенен и его включение в уравнение регрессии необходимо. В противном случае, фактор нецелесообразно включать в модель регрессии.
). Одновременно используется и обратный метод, то есть исключение факторов, ставших незначимыми. Фактор является незначимым, если его включение в уравнение регрессии только изменяет значения коэффициентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения. Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициента регрессии не изменяется (или меняется несущественно), то данный признак существенен и его включение в уравнение регрессии необходимо. В противном случае, фактор нецелесообразно включать в модель регрессии.
При построении модели регрессии возможна проблема мультиколлинеарности, под которой понимается тесная зависимость между факторными признаками, включенными в модель ( 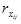 > 0,8).
> 0,8).
Наличие мультиколлинеарности между признаками приводит к:
§ искажению величины параметров модели, которые имеют тенденцию к завышению, чем осложняется процесс определения наиболее существенных факторных признаков;
§ изменению смысла экономической интерпретации коэффициентов регрессии.
В качестве причин возникновения мультиколлинеарности между признаками, можно выделить следующие:
§ изучаемые факторные признаки являются характеристикой одной и той же стороны явления или процесса. Например: показатели объема производимой продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как они оба характеризуют размер предприятия;
§ факторные признаки являются составляющими элементами друг друга;
§ факторные признаки по экономическому смыслу дублируют друг друга.
Устранение мультиколлинеарности может реализовываться через исключение из корреляционной модели одного или нескольких линейно-связанных факторных признаков или преобразование исходных факторных признаков в новые, укрупненные факторы.
Вопрос о том, какой из факторов следует отбросить, решается на основании качественного и логического анализа изучаемого явления.
Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности. Исследователь должен стремиться к увеличению числа наблюдений, так как большой объем наблюдений является одной из предпосылок построения адекватных статистических моделей.
Аналитическая форма связи результативного признака от ряда факторных выражается и называется многофакторным (множественным) уравнением регрессии или моделью связи.
Линейное уравнение множественной регрессии имеет вид:
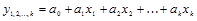 (1.9.7)
(1.9.7)
где 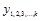 - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии;
- теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии;
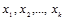 - факторные признаки;
- факторные признаки;
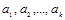 - параметры модели (коэффициенты регрессии).
- параметры модели (коэффициенты регрессии).
Параметры уравнения могут быть определены графическим методом, методом наименьших квадратов и так далее.
1.9.4 Собственно-корреляционные параметрические методы изучения связи
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторных.
Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента:
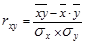 (1.9.8)
(1.9.8)
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
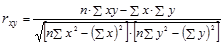 (1.9.9)
(1.9.9)
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:
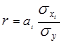 (1.9.10)
(1.9.10)
где a 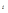 - коэффициент регрессии в уравнении связи;
- коэффициент регрессии в уравнении связи;
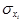 - среднеквадратическое отклонение соответствующего, статистически существенного, факторного признака.
- среднеквадратическое отклонение соответствующего, статистически существенного, факторного признака.
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: 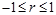 . Знаки коэффициентов регрессии и корреляции совпадают.
. Знаки коэффициентов регрессии и корреляции совпадают.
При этом интерпретацию выходных значений коэффициента корреляции можно представить в следующей таблице 1.9.3:
Таблица 1.9.3
Оценка линейного коэффициента корреляции
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |
| r = 0 | отсутствует | - |
| 0<r<1 | прямая | с увеличением x увеличивается y |
| -1<r<0 | обратная | с увеличением x уменьшается y и наоборот |
| r=1 | функциональная | каждому значению факторного признака строго соответствует одно значение результативного признака |
Пример. По исходным данным, представленным в таблице 1.9.2, оценим тесноту связи с помощью коэффициента корреляции (см. табл. 1.9.4).
Таблица 1.9.4
Расчетная таблица для определения
коэффициента корреляции
| № п/п | x | y | 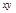
| 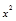
| 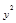
|
| 1 2 3 4 5 6 7 8 9 10 | 5 4 7 10 1 2 8 12 3 6 | 10,2 7,5 13,9 12,8 0,6 2,8 13,2 10,1 5,4 12,7 | 51 30 97,3 128 0,6 5,6 105,6 121,2 16,2 76,2 | 25 16 49 100 1 4 64 144 9 36 | 104,04 56,25 193,21 163,84 0,36 7,84 174,24 102,01 29,16 161,29 |
| Сумма | 58 | 89,2 | 631,7 | 448 | 992,24 |
| Средняя | 5,8 | 8,92 | 63,17 | 44,8 | 99,224 |
1. Используя формулу (1.9.8) получаем:
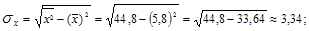
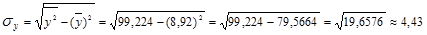
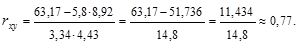
2. По формуле (1.9.9) значение коэффициента корреляции составило:
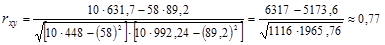
Таким образом, результат по всем формулам одинаков и свидетельствует о сильной прямой зависимости между изучаемыми признаками.
В случае наличия нелинейной зависимости между двумя признаками для измерения тесноты связи применяют теоретическое корреляционное отношение:
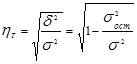 (1.9.11)
(1.9.11)
где 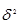 - дисперсия выравненных значений результативного признака, то есть рассчитанных по уравнению регрессии;
- дисперсия выравненных значений результативного признака, то есть рассчитанных по уравнению регрессии;
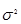 - дисперсия эмпирических (фактических) значений результативного признака.
- дисперсия эмпирических (фактических) значений результативного признака.
Для оценки тесноты связи также рассчитывается коэффициент детерминации:
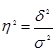 (1.9.12)
(1.9.12)
Коэффициент детерминации показывает, какая доля вариации результативного признака объясняется вариацией изучаемого фактора х.
Корреляционное отношение ( 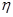 ) изменяется в пределах от 0 до 1 (
) изменяется в пределах от 0 до 1 ( 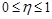 ) и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции (таблица 1.9.1).
) и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции (таблица 1.9.1).
Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трех и более признаков одновременно, вычисляется множественный и частные коэффициенты корреляции.
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков. Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле:
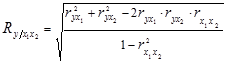 (1.9.13)
(1.9.13)
где 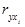 - парные коэффициенты корреляции между признаками.
- парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: 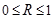 .
.
Приближение R к единице свидетельствует о сильной зависимости между признаками.
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками x 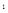 и x
и x 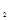 при фиксированном значении других (k − 2) факторных признаков, то есть когда влияние x
при фиксированном значении других (k − 2) факторных признаков, то есть когда влияние x 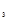 исключается, то есть оценивается связь между x
исключается, то есть оценивается связь между x 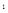 и x
и x 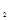 в «чистом виде».
в «чистом виде».
В случае зависимости y от двух факторных признаков x 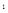 и x
и x 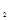 коэффициенты частной корреляции имеют вид:
коэффициенты частной корреляции имеют вид:
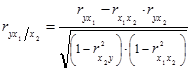
(1.9.14)
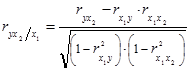
где r - парные коэффициенты корреляции между указанными в индексе переменными.
В первом случае исключено влияние факторного признака x  , во втором - x
, во втором - x  . Эти показатели могут быть и отрицательными, так как они показывают, какая существует связь между признаками: прямая или обратная.
. Эти показатели могут быть и отрицательными, так как они показывают, какая существует связь между признаками: прямая или обратная.
1.9.5 Принятие решений на основе уравнений регрессии
Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относится исследуемое явление. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков.
Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый.
Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает; если факторный признак имеет знак минус, то с его увеличением результативный признак уменьшается.
Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он имеет знак минус, то необходимо проверить расчеты параметров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных ошибок при решении. Однако следует иметь в виду, что когда рассматривается совокупное влияние факторов, то в силу наличия взаимосвязей между ними характер их влияния может меняться.
С целью расширения возможностей экономического анализа, используются частные коэффициенты эластичности, определяемые по формуле:
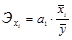 (1.9.15)
(1.9.15)
где 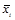 - среднее значение соответствующего факторного признака;
- среднее значение соответствующего факторного признака;
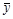 - среднее значение результативного признака;
- среднее значение результативного признака;
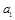 - коэффициент регрессии при соответствующем факторном признаке.
- коэффициент регрессии при соответствующем факторном признаке.
Коэффициент эластичности показывает на сколько процентов в среднем изменится значение результативного признака при изменении соответствующего факторного признака на 1%, при исключении влияния других факторов, учтенных в модели.
Частный коэффициент детерминации:
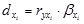 (1.9.16)
(1.9.16)
где 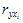 - парный коэффициент корреляции между результативным и i-ым факторным признаком;
- парный коэффициент корреляции между результативным и i-ым факторным признаком;
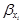 - соответствующий стандартизованный коэффициент уравнения множественной регрессии:
- соответствующий стандартизованный коэффициент уравнения множественной регрессии:
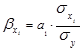 (1.9.17)
(1.9.17)
Частный коэффициент детерминации показывает на сколько процентов вариация результативного признака объясняется вариацией i-го признака, входящего в множественное уравнение регрессии.
Наиболее полная экономическая интерпретация моделей регрессии позволяет выявить резервы развития и повышения деловой активности субъектов экономики.
1.9.6 Методы изучения связи качественных признаков
При наличии соотношения между вариацией качественных признаков говорят об их ассоциации, взаимосвязанности. Для оценки связи в этом случае используют ряд показателей.
Коэффициент ассоциации и контингенции. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции.
Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, то есть состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой).
Таблица 1.9.5
Таблица для вычисления коэффициентов
ассоциации и контингенции
| у х | 0 | 1 | Итого |
| 0 | a | b | a+b |
| 1 | c | d | c+d |
| Итого | a+c | b+d | N |
Коэффициенты вычисляются по формулам:
ассоциации: 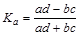 (1.9.18)
(1.9.18)
контингенции: 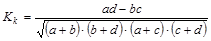 (1.9.19)
(1.9.19)
Причем, всегда коэффициент контингенции меньше коэффициента ассоциации ( 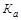 >
> 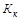 ).
).
Связь считается подтвержденной, если 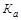
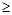 0,5 или
0,5 или 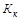
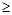 0,3.
0,3.
Пример. В результате обследования студентов факультета экономики и менеджмента БГТУ им. В.Г. Шухова получены данные, представленные в таблице 1.9.6. Определим коэффициент контингенции между успеваемостью и посещаемостью спортивных секций студентами.
Таблица 1.9.6
Зависимость успеваемости студентов от посещаемости
спортивных секций
| Успеваемость | Количество студентов | ||
| посещающих спортивные секции | не посещающих спортивные секции | Итого | |
| Удовлетворительная Неудовлетворительная | 374 17 | 102 51 | 476 68 |
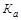 =
= 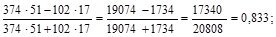
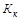 =
= 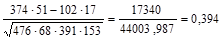
Таким образом, связь между успеваемостью и посещаемостью спортивных секций студентами факультета экономики и менеджмента имеет место, но не столь существенна.
Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова. Эти коэффициенты вычисляются по следующим формулам:
коэффициент Пирсона: 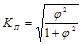 (1.9.20);
(1.9.20);
коэффициент Чупрова: 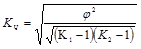 (1.9.21)
(1.9.21)
где 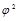 - показатель взаимной сопряженности;
- показатель взаимной сопряженности;
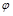 - определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот, соответствующего столбца и строки. Вычитая из этой суммы «1», получим величину
- определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот, соответствующего столбца и строки. Вычитая из этой суммы «1», получим величину 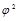 :
: 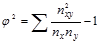 ;
;
K 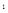 - число значений (групп) первого признака;
- число значений (групп) первого признака;
K 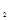 - число значений (групп) второго признака.
- число значений (групп) второго признака.
Чем ближе величина коэффициента Пирсона и коэффициента Чупрова к 1, тем теснее связь.
Таблица 1.9.7
Вспомогательная таблица для расчета коэффициента
взаимной сопряженности
| у х | I | II | III | Итого |
| I II III | 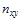
| 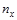
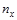
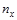
| ||
| Итого | 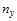
| 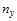
| 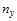
| n |
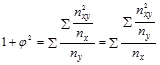 (1.9.22)
(1.9.22)
Пример. С помощью коэффициентов взаимной сопряженности исследуем связь между квалификацией рабочих предприятия и уровнем их образования (см. табл. 1.9.8).
Таблица 1.9.8
Зависимость квалификации рабочих от их уровня образования
| Квалификация | Образование | Итого | ||
| незаконченное среднее | среднее | незаконченное высшее | ||
| Низкая Средняя Высокая | 15 10 - | 5 20 15 | - 5 20 | 20 35 35 |
| Итого | 25 | 40 | 25 | 90 |
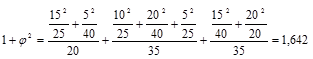
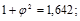
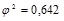
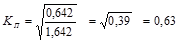 ;
; 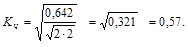
Связь умеренная.
1.9.7 Ранговые коэффициенты связи
Исследуя экономику, необходимо считаться с взаимосвязью наблюдаемых показателей и величин. При этом полнота описания, так или иначе, определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенной из них, а также воздействия одних факторов на другие является одной из основных задач статистики. Формы проявления взаимосвязей разнообразны. Одна из основных форм корреляционная (неполная, статистическая) связь.
Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак.
Ранжирование - упорядочение единиц совокупности по значению признака.
При ранжировании каждой единице совокупности присваивается ранг.
Ранг - это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической из соответствующих номеров мест, которые определяют. Данные ранги называются связными.
Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена ( 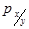 ) и Кендалла (τ). Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками.
) и Кендалла (τ). Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками.
Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле:
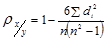 (1.9.23)
(1.9.23)
d – разность рангов признаков Х и Y;
n – число наблюдаемых единиц.
В случае отсутствия связи 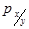 =0. При прямой связи коэффициент
=0. При прямой связи коэффициент 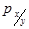 - положительная дробь, при обратной – отрицательная.
- положительная дробь, при обратной – отрицательная.
Коэффициент Спирмена принимает любые значения в интервале [−1; 1] .
Пример. По данным пятнадцати заводов, представленных в табл. 1.9.9, рассчитать коэффициент ранговой корреляции Спирмена, характеризующий степень тесноты связи между стоимостью основных фондов и выработкой цемента.
Сущность метода Спирмена состоит в следующем:
1) располагают варианты факторного признака по возрастанию - ранжируют единицы по значению признака y;
2) для каждой единицы совокупности указывают ранг с точки зрения результативного признака y .
Если связь между признаками прямая, то с увеличением ранга признака x ранг признака y также будет возрастать; при тесной связи ранги признаков x и y в основном совпадут. При обратной связи возрастанию рангов признака x будет, как правило, соответствовать убывание рангов признака y. В случае отсутствия связи последовательность рангов признака y не будет обнаруживать никакого порядка возрастания или убывания.
Таблица 1.9. 9
Исходные данные
| № п/п | Среднегодовая стоимость промышленно-производственных фондов, млн. руб. (х) | Выпуск цемента, тыс. т (у) |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 11,1 8,4 8,0 7,9 5,3 10,3 8,0 8,7 12,8 5,4 5,8 3,6 5,5 4,5 2,9 | 8,8 22,3 19,8 20,8 11,5 25,8 22,8 15,7 21,7 10,7 12,2 8,5 13,9 14,5 7,6 |
Возьмем данные по условию, занесем их в графы 1-3 табл. 1.9.10 и проведем ранжирование (распределение по рангам).
Результаты ранжирования отражены в графах 4 и 5 табл. 1.9.10.








