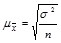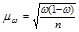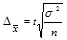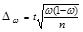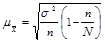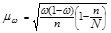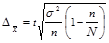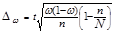1.8 Выборочное наблюдение
1.8.1 Понятие о выборочном наблюдении
В настоящее время в условиях рыночных отношений в России находит все более широкое применение наиболее совершенный и научно обоснованный способ несплошного наблюдения – выборочное наблюдение, которое используется в работе органов государственной статистики, научно-исследовательских лабораторий и предприятий. Выборочное наблюдение позволяет лучше организовать наблюдение, обеспечивает быстроту проведения, экономию труда и средств на получение и обработку информации.
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу – по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
Совокупность, из которой отбираются элементы для обследования, называют генеральной, а совокупность, которую непосредственно обследуют, – выборочной (выборка). Статистические характеристики выборочной совокупности рассматриваются как оценки соответствующих характеристик генеральной совокупности. Поскольку выборочная совокупность неточно воспроизводит структуру генеральной, то выборочные оценки также не совпадают с характеристиками генеральной совокупности. Различия между ними называют ошибками выборки.
Как и сама выборочная характеристика, ошибка выборки является случайной величиной и зависит:
1) от степени вариации изучаемого признака;
2) от численности выборочной совокупности;
3) от способа формирования выборочной совокупности;
4) от принятого уровня достоверности результата исследования.
Достоверность рассчитанных по выборочным данным характеристик в значительной степени определяется репрезентативностью выборочной совокупности, которая, в свою очередь, зависит от способа отбора единиц из генеральной совокупности. В каждом конкретном случае в зависимости от целого ряда условий, а именно, сущности исследуемого явления, объема совокупности, вариации и распределения наблюдаемых признаков, материальных и трудовых ресурсов, выбирают наиболее предпочтительную систему организации отбора, которая определяется видом, методом и способом отбора.
По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом отборе – группы единиц, а комбинированный отбор предполагает сочетание группового и индивидуального отбора.
Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора. Различают повторный и бесповторный способы отбора при формировании выборки.
При повторном отборе численность генеральной совокупности на каждом этапе отбора не изменяется (попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в генеральную совокупность для участия в дальнейшей процедуре отбора) и вероятность отбора каждой единицы остается постоянной.
При бесповторном отборе вероятность попадания каждой единицы в выборку увеличивается по мере процедуры отбора (попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор).
1.8.2 Способы формирования выборочной совокупности
Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности. В практике выборочных обследований наибольшее распространение получили следующие выборки:
§ собственно-случайная;
§ механическая;
§ типическая;
§ серийная;
§ многоступенчатая;
§ многофазная.
Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или невключение в нее отдельных единиц не вызывало сомнений.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел. Для жеребьевки необходимо подготовить достаточное количество жребиев – фишек, шаров, карточек, соответствующее объему генеральной совокупности. Каждый жребий должен содержать информацию об отдельной единице совокупности – номер, фамилию лица или адрес, название или какой-либо другой отличительный признак. Необходимое в соответствии с установленным процентом отбора количество жребиев извлекается из общей их совокупности в случайном порядке.
При отборе по таблицам случайных чисел каждая единица генеральной совокупности должна иметь порядковый номер. Таблицы случайных чисел получаются с помощью датчика случайных чисел на ПК и представляют собой абсолютно произвольные столбцы цифр. В соответствии с объектом генеральной совокупности выбирается любой столбец с числами необходимой значимости. Например, если генеральная совокупность включает 5000 единиц, потребуются четырехзначные столбцы, при этом числа больше 5000 не будут приниматься во внимание. В выборочную совокупность отбираются единицы с порядковыми номерами, соответствующими числам выбранного столбца.
Собственно-случайный отбор может быть как повторным, так и бесповторным. Для проведения бесповторного отбора в процессе жеребьевки выпавшие жребии обратно в исходную совокупность не возвращаются и в дальнейшем отборе не участвуют. При использовании таблиц случайных чисел бесповторность отбора достигается пропуском чисел в случае их повторения в выбранном столбце или столбцах. После проведения отбора для определения возможных границ генеральных характеристик рассчитываются средняя и предельная ошибки выборки. Формулы расчета ошибок выборки и основные характеристики параметров генеральной и выборочной совокупности представлены в таблице 1.8.1.
Как видно из формул (табл. 1.8.1), размер предельной ошибки зависит от вариации признака 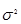 , объема выборки n и ее доли в генеральной совокупности
, объема выборки n и ее доли в генеральной совокупности 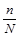 , а также принятого уровня вероятности (р), которому соответствует коэффициент кратности t. Так, t=1 для вероятности 0,683; t=2 для вероятности 0,954; t=3 для вероятности 0,997.
, а также принятого уровня вероятности (р), которому соответствует коэффициент кратности t. Так, t=1 для вероятности 0,683; t=2 для вероятности 0,954; t=3 для вероятности 0,997.
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для генеральной средней такие пределы устанавливаются на основе следующих соотношений: 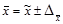 (1.8.1)
(1.8.1)
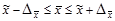 , (1.8.2)
, (1.8.2)
где 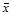 и
и 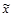 - генеральная и выборочная средняя соответственно;
- генеральная и выборочная средняя соответственно;
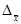 - предельная ошибка генеральной средней.
- предельная ошибка генеральной средней.
Доверительные интервалы для генеральной доли:
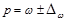 (1.8.3)
(1.8.3)
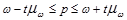 (1.8.4)
(1.8.4)
Таблица 1.8.1
Формулы расчета ошибок выборки и основные характеристики
параметров генеральной и выборочной совокупности
|
| Способ отбора единиц | Характеристики | |||
| повторный | бесповторный | объем сово-куп-ности | доля еди- ниц | средний размер приз- нака | |
| Средняя ошибка ( для средней
для доли
Преде-льная ошибка ( для средней
для доли |
|
| Генеральная совокупность | ||
| N |
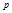
|
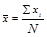
| |||
| Выборочная совокупность | |||||
| n | 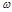
|
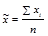
| |||
Покажем практическое применение рассмотренной выше методики на следующем примере.
Пример: по итогам проведенной 10%-й случайной выборки получено следующее распределение работников фирмы по уровню заработной платы (см. табл. 1.8.2).
Таблица 1.8.2
| Группы работников по уровню заработной платы, тыс. руб. | до 1,0 | 1,0 – 1,5 | 1,5 – 2,5 | 2,5 – 5,0 | 5,0 и более | Итого |
| Число работников | 5 | 12 | 35 | 43 | 15 | 110 |
1) Определить с вероятностью 0,954 пределы средней заработной платы работников данной фирмы;
2) С вероятностью 0,95 границы доли работников, имеющих заработную плату не более 1,5 тыс. руб.
Решение:
1. Вначале, на основе имеющегося распределения работников, определим выборочные среднюю и дисперсию. Для этого построим дополнительную расчетную таблицу 1.8.3:
Таблица 1.8.3
Группы работников по уровню заработной платы,
тыс. руб.
х 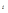
| Число работников
f 
| Сере-дина интер-
вала
( 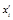 ) )
| 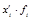
| 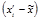
| 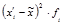
|
| до 1,0 1,0 – 1,5 1,5 – 2,5 2,5 – 5,0 5,0 и более | 5 12 35 43 15 | 0,75 1,25 2,0 3,75 6,25 | 3,75 15,0 70,0 161,25 93,75 | -2,65 -2,15 -1,40 0,35 2,85 | 35,1 55,5 68,6 5,27 121,8 |
| Итого | 110 | 343,75 | 286,3 |
Определим выборочную среднюю:
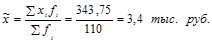
Рассчитаем выборочную дисперсию:
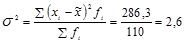
Рассчитаем среднюю ошибку выборки:
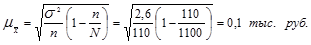
Вычислим теперь предельную ошибку выборки (с учетом того, что при р=0,954 t=2):
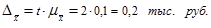
Следовательно, доверительный интервал будет следующим:
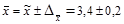 ;
;
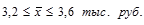
Таким образом, с вероятностью 0,954 можно утверждать, что средняя заработная плата работников исследуемой фирмы находиться в пределах от 3,2 до 3,6 тыс. руб.
2. Определим выборочную долю: 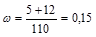
Вычислим среднюю ошибку доли:
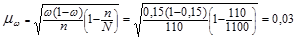
Рассчитаем предельную ошибку доли:
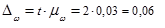
Построим доверительный интервал:
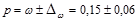 ;
;
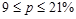 .
.
Таким образом, с вероятностью 0,95 можно утверждать, что доля работников, имеющих заработную плату не более 1,5 тыс. руб. находится в пределах от 9% до 21%.
Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.).
Отбор элементов осуществляется через одинаковые интервалы, шаг интервала зависит от доли выборки. Так, при 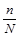 = 0,05 шаг интервала составляет
= 0,05 шаг интервала составляет 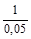 = 20. Ошибка механической выборки вычисляется по формуле бесповторной выборки. Для моментных наблюдений, фиксирующих состояние непрерывного процесса на определенные моменты времени, используют формулу ошибки повторной выборки.
= 20. Ошибка механической выборки вычисляется по формуле бесповторной выборки. Для моментных наблюдений, фиксирующих состояние непрерывного процесса на определенные моменты времени, используют формулу ошибки повторной выборки.
При типическом отборе генеральная совокупность разбивается на несколько типических групп по существенному признаку. При обследовании населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасль или подотрасль, форма собственности и т.п. Затем из каждой группы путем собственно-случайного или механического отбора отбираются единицы в выборочную совокупность.
При вычислении ошибки типической выборки используют среднюю из групповых дисперсий:
для средней: 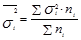 (1.8.5);
(1.8.5);
для доли: 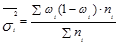 (1.8.6)
(1.8.6)
Средняя ошибка типической выборки определяется следующим образом:
для средней: 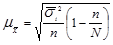 (1.8.7);
(1.8.7);
для доли: 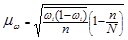 (1.8.8)
(1.8.8)
Как правило, 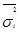 <
< 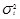 , следовательно, ошибка типической выборки меньше, чем механической или простой случайной. Чаще всего используют отбор, пропорциональный численности составляющих совокупности, т. е. доля выборки для всех составляющих одинакова.
, следовательно, ошибка типической выборки меньше, чем механической или простой случайной. Чаще всего используют отбор, пропорциональный численности составляющих совокупности, т. е. доля выборки для всех составляющих одинакова.
Серийный отбор удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться районы, поселки, фирмы, акционерные общества, студенческие группы, бригады, а также упаковки с определенным количеством готовой продукции, партии товара и т.д. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:
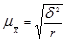 - повторный отбор (1.8.9);
- повторный отбор (1.8.9);
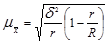 - бесповторный отбор (1.8.10),
- бесповторный отбор (1.8.10),
где r – число отобранных серий;
R – общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:
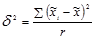 (1.8.11),
(1.8.11),
где 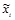 - средняя i-й серии;
- средняя i-й серии;
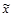 - общая средняя по всей выборочной совокупности.
- общая средняя по всей выборочной совокупности.
При серийном отборе ошибка будет меньше, чем при механическом отборе.
Многоступенчатая выборка предполагает извлечение из генеральной совокупности сначала укрупненных групп единиц, затем групп, меньших по объему, и так до тех пор, пока не будут отобраны те группы (серии) или отдельные единицы, которые будут подвергнуты наблюдению. Выборка может быть двухступенчатой, когда генеральная совокупность разбивается на группы и производится отбор групп, а затем внутри групп – отбор единиц наблюдения. На обеих ступенях отбор может вестись в случайном порядке. В этом случае ошибка рассчитывается следующим образом:
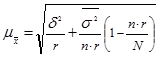 (1.8.12)
(1.8.12)
В отличие от типического отбора, где отбор производится из всех без исключения групп, при многоступенчатом отборе производится отбор самих групп, и, следовательно, не все они попадают в выборку.
Число ступеней отбора может быть и более трех. Если число ступеней отбора больше двух, то средняя ошибка выборки определяется по формуле:
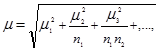 (1.8.13)
(1.8.13)
где 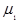 ,
, 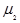 ,
, 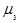 - средние ошибки выборки на отдельных ступенях отбора;
- средние ошибки выборки на отдельных ступенях отбора;
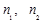 - численность выборок на соответствующих ступенях.
- численность выборок на соответствующих ступенях.
Многофазная выборка отличается от многоступенчатой тем, что на каждой стадии сохраняется одна и та же единица отбора, но изменяется программа наблюдения. Причем расширенная программа обязательно содержит вопросы краткой программы, что делает возможным проверить репрезентативность выборки. Расчет ошибки многофазной выборки производится для каждой фазы в отдельности.
1.8.3 Определение необходимого объема выборки
В практике проектирования выборочного наблюдения возникает вопрос о необходимой численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки.
При случайном повторном отборе численность выборки определяется по формуле:
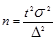 (1.8.14)
(1.8.14)
При случайном бесповторном и механическом отборе численность выборки вычисляется по формуле:
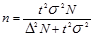 (1.8.15)
(1.8.15)
Для типической выборки:
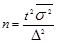 - повторный отбор (1.8.16);
- повторный отбор (1.8.16);
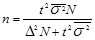 - бесповторный отбор (1.8.17)
- бесповторный отбор (1.8.17)
Для серийной выборки:
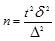 - повторный отбор (1.8.18);
- повторный отбор (1.8.18);
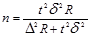 - бесповторный отбор (1.8.19)
- бесповторный отбор (1.8.19)
При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.
Основные вопросы, решаемые при расчете численности выборки:
1)необходимо принять решение о размере допустимой погрешности;
2)коэффициент кратности t определяется согласно принятой вероятности результата исследований;
3)в приведенных формулах вместо фактических значений дисперсии и доли используются приблизительные значения, полученные на основе ранее проводимых исследований, либо на основе пробных выборок.
4)если планируется выборка для исследования доли альтернативного признака, то в формулы подставляется максимально возможное значение дисперсии;
5)расчет численности выборки производится несколько раз, исходя из требований точности для всех изучаемых признаков. В качестве окончательного решения выбирается наибольшее из полученных значений;
6)если полученные значения n различаются в 6, 7 и более раз, то выборка организуется как многоступенчатая;
7)если объем генеральной совокупности достаточно велик (более 100 тыс.), то используются формулы для повторного отбора независимо от типа планируемой выборки.
Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.
Пример 1. В районе проживает 2500 семей. Предполагается провести их выборочное обследование методом случайного бесповторного отбора для нахождения среднего размера семьи. Определить необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит одного человека при среднем квадратическом отклонении три человека.
Решение. При бесповторном случайном отборе необходимый объем выборки по формуле (1.8.15) составит:
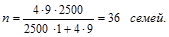
Пример 2. В городе А проживает 15 тыс. семей. С помощью механической выборки предполагается определить долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка выборки не превышала 0,04, если на основе предыдущих обследований известно, что дисперсия равна 0,3?
Решение. Определим необходимую численность выборки по формуле (1.8.15):
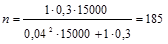
Пример 3. С целью определения доли рабочих акционерного общества области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число рабочих акционерного общества составляет 15 тыс. чел., в том числе 9 тыс. мужчин и 6 тыс. женщин.
На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1800. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Решение. Рассчитаем общую численность типической выборки по формуле (1.8.17):
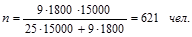
Вычислим теперь объем отдельных типических групп:
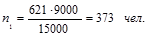
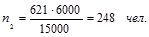
Таким образом, необходимый объем выборочной совокупности рабочих акционерного общества области составляет 621 чел., в т. ч. 373 мужчин и 248 женщин.
Пример 4. В коммерческом банке 230 отделов с работниками. Планируется проведение выборочного обследования с целью определения удельного веса работников, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество отделов для обследования работников, если ошибка выборки не должна превышать 5%.
Решение. Необходимое количество отделов рассчитаем на основе формулы объема серийной бесповторной выборки по формуле (1.8.19):
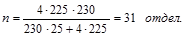
Тренировочные задания
1. Из партии муки в порядке случайной повторной выборки было взято 30 проб. В результате проверки установлена средняя влажность муки в выборке, равная 14,5% (при среднем квадратическом отклонении, равном 2%). С вероятностью 0,683 определите пределы средней влажности во всей партии муки.
Решение:
Для решения этой задачи необходимо воспользоваться следующим соотношением:
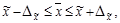
где 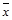 и
и 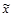 - генеральная и выборочная средние соответственно;
- генеральная и выборочная средние соответственно;
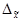 - предельная ошибка выборочной средней.
- предельная ошибка выборочной средней.
Чтобы рассчитать среднюю ошибку при случайном повторном отборе воспользуемся формулой:
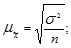
Для расчета предельной ошибки воспользуемся следующей формулой:
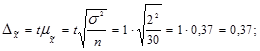
при этом t=1, т.к. р=0,683; 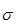 =2; n=30.
=2; n=30.
Отсюда получаем следующее соотношение:
14,5 - 0,37 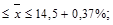
14,13 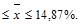
Таким образом, средняя влажность муки во всей партии колеблется в следующих пределах: 14,13 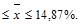
2. Для определения средней продолжительности поездки на работу планируется провести выборочное обследование населения г. Белгорода методом случайного бесповторного отбора. Численность работающего населения г. Белгорода составляет 153,4 тыс. чел. Каков должен быть необходимый объем выборочной совокупности, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 мин. При среднем квадратическом отклонении 15 мин.
Решение:
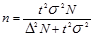 ;
;
t=2, т.к. р=0,954;
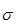 =15; N=153,4;
=15; N=153,4; 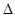 =5;
=5;
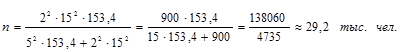
3. За одну смену АО «Колос» выпустил 15000 буханок хлеба, каждая по 800 грамм. Предполагается провести обследование среднего веса буханки методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка не превышала 20 грамм, если по данным пробного обследования дисперсия составила 240?
4. Для обследования качества, продукция была распределена на 75 равновеликих серий. На основе механического отбора было проверено 15 серий, в которых удельный вес недоброкачественной продукции составил 15%. С вероятностью 0,683 установите границы качества всей продукции, если межсерийная дисперсия равна 860.
5. Для изучения общественного мнения населения области о проведении определённых мероприятий методом случайного отбора было опрошено 1000 человек. Из числа опрошенных 540 человек одобрили мероприятия.
С вероятностью 0,954 определите пределы, в которых находится доля лиц, одобривших мероприятия.
6. При планировании выборочного обследования занятости населения сельских районов региона имеются следующие данные:
| Район | Численность населения в трудоспособном возрасте, тыс. чел. | Удельный вес занятого населения, % (оценка) |
| 1 | 4,2 | 70 |
| 2 | 7,3 | 82 |
| 3 | 3,5 | 75 |
| 4 | 5,8 | 80 |
С вероятностью 0,997 определите необходимый объём типической пропорциональной выборки для установления границ генеральной доли, чтобы ошибка выборки не превышала 5%.
7. Партия елочных гирлянд упакована в 300 коробок по 20 шт. в каждой. Средняя длительность горения гирлянд составляет 1100 ч, а межсерийная дисперсия – 250. Качество гирлянд проверяется на основе серийного 2%-ного случайного бесповторного отбора.
Определите:
а) предельную ошибку при установлении средней длительности горения гирлянд;
б) пределы контролируемого параметра в генеральной совокупности.
Выводы сделайте с вероятностью 0,997.
8. Определите, сколько персональных компьютеров следует подвергнуть обследованию в порядке случайной бесповторной выборки, чтобы с вероятностью 0,954 предельная ошибка (в процентах к среднему сроку службы компьютера) не превышала 3%. Коэффициент вариации среднего срока службы компьютеров по данным предыдущих обследований составляет 15%, а вся партия состоит из 1250 компьютеров.
9. По данным 20% выборочного обследования 100 семей переселенцев из зоны строгого радиационного контроля, количество детей в семьях составляет:
| Количество детей | 0 | 1 | 2 | 3 | 4 | Итого |
| Количество семей | 10 | 32 | 33 | 18 | 7 | 100 |
Определите:
1) среднее количество детей в семьях переселенцев и доверительный интервал для средней с вероятностью 0,954;
2) с той же вероятностью определите предельную ошибку, и доверительный интервал для доли семей, имеющих 3 и более детей.
10. При случайном способе отбора из партии было взято 100 проб продукта А. В результате обследования установлено, что доля брака продукта А в выборке составляет 2%. С вероятностью 0,954 определите пределы, в которых находится доля брака продукта А в партии.
11. Для определения среднего возраста рабочих предприятия была произведена 10%-ная механическая выборка рабочих методом случайного бесповторного отбора. В результате обследования были получены следующие данные:
| Рабочие в возрасте, лет | 20 - 30 | 30 - 40 | 40 - 50 | 50 – 60 | Итого |
| Число рабочих, чел. | 20 | 60 | 15 | 5 | 100 |
С вероятностью 0,997 определите:
1) пределы, в которых находится средний возраст рабочих предприятия;
2) пределы, в которых находится доля рабочих предприятия в возрасте старше 50 лет.
12. По результатам контрольной проверки налоговыми службами 500 бизнесструктур, у 175 из них в налоговых декларациях не полностью указаны доходы, подлежащие налогообложению.
Определите долю бизнесструктур, скрывших часть доходов от уплаты налогов, и доверительные границы доли с вероятностью 0,997.
13. Для выявления затрат времени на обработку деталей рабочими разной квалификации на предприятии была произведена 10%-я типическая выборка пропорционально численности выделенных групп (внутри типических групп произведён механический отбор). Результаты обследования могут быть представлены следующим образом:
| Группы рабочих по разряду | Число рабочих | Средние затраты времени на обработку одной детали, мин. | Среднее квадратическое отклонение, мин. |
| I | 30 | 10 | 1 |
| II | 50 | 14 | 4 |
| III | 20 | 20 | 2 |
С вероятностью 0,954 определите пределы, в которых находятся средние затраты времени на обработку деталей рабочими.
14. По данным опроса из 400 респондентов, основными источниками информации о недвижимости считают:
Радио и телевидение............................................................ ...120
Газеты и журналы.................................................................. 180
Интернет…………………..................................................... 100
Для каждого источника информации определите его долю и предельную ошибку выборки с вероятностью 0,997.
15. С целью прогнозирования урожая овса в хозяйстве была произведена 10%-я серийная выборка, в которую попали три участка. В результате обследования установлено, что урожайность овса на участках составила 26, 30 и 34 ц/га. С вероятностью 0,954 определите пределы, в которых будет находиться средняя урожайность овса в хозяйстве.
16. При обследовании семейных бюджетов населения города была организована 10%-ная типическая пропорциональная выборка. Результаты обследования представлены в следующей таблице:
| Группы населения по семейному положению | Объем выборки | Доля расходов на оплату жилья, % |
| Одинокие Семейные | 55 145 | 9 6 |
С вероятностью 0,683 установите границы доли расходов на оплату жилья населением города.
Тест
1. Как называется статистическая совокупность, из которой производится отбор?
а) генеральная;
б) выборочная.
2. Доверительный интервал выборочной средней и доли при малой выборке является односторонним или двусторонним?
а) односторонним;
б) двусторонним.
3. При выборочном обследовании бюджета времени работающих отбирается каждое пятое предприятие из общего списка их отрасли, а затем на отобранных предприятиях отбирается каждый десятый рабочий или служащих. Укажите способ такого отбора:
а) механический;
б) типический;
в) многоступенчатый;
г) многофазный;
д) многомерный.
4. Различия между выборочными оценками и характеристиками генеральной совокупности называются:
а) ошибками регистрации;
б) ошибками репрезентативности.
5. Ошибка механической выборки вычисляется по формуле:
а) повторной выборки;
б) бесповторной выборки.
6. Определите предельную ошибку выборки с вероятностью 0,9, если средняя ошибка равна 100:
а) 90; б) 164; в) 200.
7. По данным выборочного обследования 25 фирм (19%-й отбор) средняя продолжительность оборота дебиторской задолженности – 72 дня при среднем квадратическом отклонении 10 дней. Определите предельную ошибку выборки для средней продолжительности оборота с вероятностью 0,954.
а) 1,8; б) 2,0;
в) 3,6; г) 4,0.
8. При вычислении ошибки типической выборки используют:
а) общую дисперсию;
б) среднюю из групповых дисперсий;
в) межгрупповую дисперсию.
9. С вероятностью 0, 954 определить необходимую численность выборки для оценки среднего размера семьи при условии, что ошибка выборочной средней не должна превышать 0,5 чел. при среднем квадратическом отклонении 2,0 чел.
а) 64; б) 45; в) 57.
10. При каком отборе одни и те же единицы подвергаются обследованию по расширенной программе?
а) при комбинированном;
б) при многоступенчатом;
в) при многофазном;
г) при механическом.
11. Определите с вероятностью 0,95 предельную ошибку, если средняя ошибка равна 30:
а) 28,5; б) 58,8; в) 60,0.
12. В каком случае предельная ошибка доли признака в генеральной совокупности будет больше (при прочих равных условиях), если общая дисперсия в 3,5 раза больше межгрупповой:
а) при отборе 100 единиц;
б) при отборе 25 серий.
13. Что произойдет с предельной ошибкой выборки, если вероятность, гарантирующую результат, увеличить с 0,683 до 0,954?
а) увеличится на 27%;
б) увеличится в 1,4 раза.
в) увеличится в два раза;
г) уменьшится в два раза;
14. Обследовано 36% продукции предприятия. На сколько процентов ошибка собственно случайной бесповторной выборки меньше ошибки повторной выборки?
а) 36; б) 20;
в) 18; г) 6;
д) предсказать результат невозможно.
15. С вероятностью 0,997 определите предельную ошибку выборки, если известно, что средняя ошибка равна 50.
а) 100; б) 50,997;
в) 150; г) 49,85.
16. При прочих равных условиях ошибка выборки будет меньше при:
а) механическом отборе;
б) типическом отборе;
в) серийном отборе.
17. Сколько респондентов необходимо опросить, оценивая качество гостиничного обслуживания (удовлетворяет, не удовлетворяет), чтобы предельная ошибка выборки долей с вероятностью 0,954 при этом не превысила 5%?
а) 400; б) 100;
в) 200; г) 20.
18. Из партии готовой продукции в 1000 шт. в случайном бесповторном порядке обследовано 100 штук. Доля забракованных изделий составила 10%. Определите вероятность того, что допущенная погрешность не превысит 5%
а) t=1,67;
б) t=1,76;
в) t=2,0
19. Для каких способов формирования выборочной совокупности ошибка выборки определяется по одинаковым формулам?
а) для собственно-случайного и механического;
б) для собственно–случайного и типического;
в) для механического и типического.
20. По данным выборочного опроса 46% респондентов считают рекламу основным источником информации о товарном рынке. Средняя ошибка выборки этого показателя – 2,5%. С вероятностью 0,954 можно утверждать, что рекламой пользуются:
а) не менее 43,5% потребителей;
б) не более 48,5%;
в) не менее 41 и не более 51%;
г) не менее 51%.
1.9 Статистические методы изучения взаимосвязей
социально-экономических явлений
1.9.1 Причинность, регрессия, корреляция
Исследование объективно существующих зависимостей и взаимосвязей между явлениями и процессами - важнейшая задача теории статистики, которая играет в экономике значительную роль и позволяет глубже понять сложный механизм причинно-следственных отношений между явлениями. Причинно-следственные отношения - это такая связь явлений и процессов, когда изменение одного из них - причины ведет к изменению другого - следствия.
Все социально-экономические явления взаимосвязаны и представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих явлений необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.
Признаки по их значению для изучения взаимосвязи делятся на два класса. Признаки, характеризующие причины и условия связи, называются факторными (х), а признаки, которые характеризуют следствия связи, – результативными (у).
Между признаками х и у возникают разные по природе и характеру связи, а именно: функциональные и стохастические. При функциональной связи каждому значению признака х соответствует одно определенное значение у. Эта связь проявляется однозначно в каждом отдельном случае. При стохастической связи каждому значению признака х соответствует определенное множество значений у, образующих так называемое условное распределение. Как закон эта связь проявляется только в массе случаев и характеризуется изменением условных распределений у. Если заменить условное распределение средней величиной 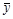 , то образуется разновидность стохастической связи – корреляционная. В случае корреляционной связи каждому значению признака х соответствует среднее значение результативного признака
, то образуется разновидность стохастической связи – корреляционная. В случае корреляционной связи каждому значению признака х соответствует среднее значение результативного признака 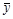 .
.
Связи между явлениями и их признаками классифицируются:
§ по степени тесноты;
§ по направлению;
§ по аналитическому выражению.
По степени тесноты связи представлены в таблице 1.9.1.
По направлению выделяют:
§ Прямую связь - это такая связь, при которой с увеличением или с уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. Так, например, рост производительности труда способствует увеличению уровня рентабельности производства.
§ Обратную связь – это такая связь, при которой значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. Так с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции.
Таблица 1.9.1
Количественные критерии оценки тесноты связи
| Величина коэффициента корреляции | Характер связи |
| до ±0,3 | практически отсутствует |
| ±0,3 - ±0,5 | слабая |
| ±0,5 - ±0,7 | умеренная |
| ±0,7 - ±1,0 | сильная |
По аналитическому выражению выделяют связи:
§ прямолинейные (или просто линейные);
§ нелинейные.
Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида:
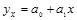 (1.9.1)
(1.9.1)
Если же связь может быть выражена уравнением какой-либо кривой линии, например, параболы, то такую связь называют нелинейной или криволинейной:
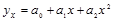 (1.9.2)
(1.9.2)
Для выявления наличия связи, ее характера и направления в статистике используются методы:
§ приведения параллельных данных;
§ аналитических группировок;
§ графический;
§ корреляции.
Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере. Сравним изменение двух величин:
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 5 | 9 | 6 | 10 | 14 | 17 | 15 | 20 | 23 |
Мы видим, что с увеличением величины X величина Y также возрастает. Можно сделать предположение, что связь между ними прямая и что ее можно описать или уравнением прямой или уравнением параболы второго порядка.
Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат - результативного.
Каждое пересечение линий, проводимых через эти оси, обозначаются точкой. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.
Корреляция - это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению среднего значения другой.
Варианты корреляционной зависимости:
1) парная корреляция - связь между двумя признаками (результативным и факторным, или двумя факторными).
2) частная корреляция - зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.
3) множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.
Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции, которые, давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии.
Регрессия тесно связана с корреляцией: первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму.
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком), обусловлено влиянием одной или нескольких независимых величин (факторов).
Одной из проблем построения уравнений регрессии является их размерность, то есть определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным.
Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, быстрее и качественнее реализуемую. В то же время, построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс.









 ):
): ):
):