Медиана дискретного вариационного ряда определяется по сумме накопленных частот, которая должна превышать половину всего объема единиц совокупности.
Так, в примере 2 половина объема совокупности равна 97,5. Первое значение, превышающее 97,5 в графе «сумма накопленных частот» - 119. Оно соответствует цене – 24 долл. США, которая и является медианой.
Для интервальных вариационных рядов медиана рассчитывается по следующей формуле:
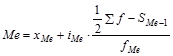 , (1.6.7)
, (1.6.7)
где Ме - медиана;
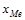 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
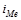 - величина медианного интервала;
- величина медианного интервала;
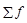 - сумма частот ряда;
- сумма частот ряда;
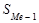 - сумма накопленных частот ряда, предшествующих медианному интервалу;
- сумма накопленных частот ряда, предшествующих медианному интервалу;
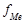 - частота медианного интервала.
- частота медианного интервала.
По данным примера 3 рассчитаем медиану для интервального вариационного ряда.
Определяем медианный интервал, в котором находится порядковый номер медианы. Для этого подсчитаем сумму частот накопленным итогом до числа, превышающего половину объема совокупности (260/2=130).
В графе «сумма накопленных частот» значение 140 соответствует интервалу 700 – 800 долл. США. Это и есть медианный интервал, в котором находится медиана.
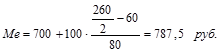
Таким образом, половина работников предприятия имеют заработную плату до 787,5 руб., а половина – выше этой суммы.
Моду и медиану можно определить на основе графического изображения ряда. Медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной.
Мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Абсцисса пересечения этих прямых и будет модой распределения.
Тренировочные задания
1. Имеются следующие данные о заработной плате и численности рабочих по двум предприятиям отрасли:
| № п/п | Базисный период | Отчетный период | ||
| Средняя списочная численность рабочих, чел. | Средняя месячная заработная плата, руб. | Фонд заработной платы, тыс. руб. | Средняя месячная заработная плата, руб. | |
| 1 2 | 620 590 | 4680 4820 | 2952 2955 | 4800 4925 |
Определите среднюю заработную плату рабочих по двум предприятиям в базисном и отчетном периодах. Укажите, какой вид средних надо применить в каждом случае.
Решение:
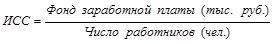
Среднюю заработную плату рабочих по двум предприятиям в базисном году будем определять по средневзвешенной арифметической формуле, так как нам неизвестен числитель исходного соотношения:
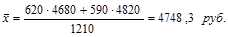
Среднюю заработную плату рабочих по двум предприятиям в отчетном году будем определять по средневзвешенной гармонической формуле, так как нам неизвестен знаменатель исходного соотношения:
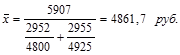
2. По приведенным данным определите средний процент выполнения договорных обязательств поставщиками комплектующих изделий. Обоснуйте выбор формулы средней:
| Комплектующие изделия | Объем договорных обязательств, млн. ден. ед. | Выполнение договорных обязательств, % |
| Двигатели | 35 | 97,8 |
| Электроника | 22 | 98,5 |
3. Следующие данные характеризуют возрастную структуру сотрудников предприятия:
| Возраст, лет | Численность сотрудников предприятия (в % к итогу) |
| до25 25 – 30 30 – 35 35 – 40 40 – 45 45 – 50 50 – 55 55 и более | 12,2 18,3 30,7 11,5 10,8 8,6 5,8 2,1 |
| Итого | 100,0 |
Определите средний возраст сотрудников предприятия.
4. Имеются следующие данные о распределении студентов по росту:
| Рост, см | Численность студентов, чел. |
| до 162 162 – 166 166 – 170 170 – 174 174 – 178 178 – 182 182 и более | 20 55 90 125 130 50 10 |
| Итого | 480 |
Определите средний рост студентов, моду и медиану роста студентов.
5. Имеются следующие данные о распределении населения Белгородской области по возрастным группам (на 1 января 2004 года):
| в % к итогу | |
| Все население в том числе в возрасте, лет до 10 10 – 20 20 – 30 30 – 40 40 – 50 50 – 60 60 – 70 70 и старше | 100,0 8,6 15,1 14,4 13,2 16,8 11,4 10,4 10,1 |
Определите величину среднего возраста населения области, а также моду и медиану. Постройте гистограмму и кумуляту распределения.
6. Продукция, производимая малым предприятием, имеет разный уровень рентабельности реализации. В апреле этот показатель составил:
| Продукция | Рентабельность реализации продукции, % | Прибыль, тыс. руб. |
| A Б B | 12 7 21 | 600 140 630 |
Определите средний уровень рентабельности реализации продукции. Обоснуйте выбор формы средней.
7. Ввод в действие жилых домов организациями различных форм собственности по Белгородской области в 2003 году  характеризуется показателями:
характеризуется показателями:
| Форма собственности | Введено в действие жилых домов в 2003 году, тыс. кв. м. | Введено в действие жилых домов в 2003 году по сравнению с 2002 годом, % |
| Государственная | 48,9 | 83,4 |
| Муниципальная | 51,6 | 144,1 |
| Частная | 558,2 | 98,3 |
| Смешанная российская | 1,4 | 127,3 |
 // Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 150
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 150
Определите средний процент ввода жилья по четырем видам собственности в 2003 году по сравнению с 2002 годом.
8. Уровни страхового возмещения в зависимости от вида имущественного риска составляют:
| Коммерческие страховые компании | Имущественный риск | |||
| Аварии и взрывы | Пожары | |||
| Процент страхового возмещения | Сумма страхового возмещения, млн. руб. | Процент страхового возмещения | Сумма страхового возмещения, млн. руб. | |
| Региональные Центральные | 0,3 0,6 | 0,24 0,42 | 0,5 0,8 | 0,80 0,56 |
Определите средний процент страхового возмещения по каждому виду риска. Сравните и объясните результаты.
9. Распределение новорожденных по возрасту матери характеризуется следующими данными:
| Возраст матери, лет | % к итогу | |
| город | село | |
| до 20 20 – 25 25 – 30 30 – 35 35 – 40 40 и старше | 14,0 40,0 27,1 13,2 4,7 1,0 | 19,5 43,1 22,1 10,4 4,0 0,9 |
| Итого | 100,0 | 100,0 |
Отдельно для городов и сел определите медианное значение возраста матери, сравните полученные результаты.
10. По данным выборочного обследования получены данные о распределении городского и сельского населения по числу детей:
| Число детей | Население, % | |
| городское | сельское | |
| 0 | 6 | 5 |
| 1 | 27 | 20 |
| 2 | 24 | 31 |
| 3 | 22 | 26 |
| 4 | 11 | 9 |
| 5 | 6 | 5 |
| 6 и более | 4 | 4 |
| Итого: | 100 | 100 |
Определите для городского и сельского населения:
1) среднее число детей в семье;
2) моду и медиану.
11. Распределение малых предприятий региона по размеру прибыли характеризуется следующими данными:
| Чистая прибыль, млн. руб. | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | свыше 60 | Итого |
| Удельный вес предприятий, % | 4 | 12 | 36 | 24 | 16 | 8 | 100 |
Определите среднюю прибыль малого предприятия.
Тест
1. Условием применения средних величин не является:
а) наличие качественно однородной совокупности;
б) достаточно большой объем совокупности;
в) группировка единиц совокупности по изучаемому признаку.
2. Частости – это:
а) абсолютные величины;
б) относительные величины;
в) средние величины.
3. Назовите степенные средние:
а) средняя арифметическая и средняя гармоническая;
б) простая и динамическая;
в) мода и медиана.
4. Выберите правильную формулу средней арифметической взвешенной:
а) 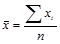 ; б)
; б) 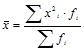 ;
;
в) 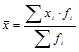 ; г)
; г) 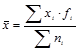 .
.
5. В каких случаях используется средняя гармоническая взвешенная?
а) когда неизвестен числитель исходного соотношения;
б) когда неизвестен знаменатель исходного соотношения.
6. Изменится ли средняя величина, если все веса уменьшить на 20%?
а) изменится;
б) не изменится.
7. Назовите структурные средние:
а) мода и медиана;
б) средняя агрегатная и средняя арифметическая;
в) средняя геометрическая и средняя квадратическая.
8. Для дискретного вариационного ряда мода – это:
а) значение изучаемого признака чаще всего встречающееся в ряду распределения;
б) варианта с наибольшей частотой;
в) значение изучаемого признака, расположенного в середине ряда распределения.
9.Если средняя рассчитывается по вторичным (сгруппированным) данным, то применяется:
а) простая форма средней;
б) взвешенная форма средней;
в) средняя геометрическая.
10. Как изменится средняя величина, если все варианты признака уменьшить в 1,5 раза, а все веса в 1,5 раза увеличить?
а) не изменится; б) уменьшится; в) возрастет.
11. В каких случаях используется средняя арифметическая взвешенная?
а) когда неизвестен числитель исходного соотношения;
б) когда неизвестен знаменатель исходного соотношения.
12.Изменится ли значение средней величины при пропорциональном изменении всех весов:
а) да;
б) нет.
13. Если все индивидуальные значения признака уменьшить на 20%, то средняя величина:
а) уменьшится; б) увеличится; в) не изменится.
14. Имеются следующие данные о распределении длины пробега автофургона торгово-посреднической фирмы за один рейс:
| Длина пробега за один рейс, км | 50 | 70 | 90 | 110 | 130 | 150 | Всего |
| Число рейсов за квартал | 20 | 25 | 14 | 18 | 9 | 6 | 92 |
Определить моду и медиану:
а) М 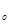 = 70 км, М
= 70 км, М 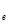 = 90 км;
= 90 км;
б) М 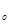 = 70 км, М
= 70 км, М 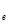 = 70 км;
= 70 км;
в) М 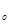 = 90 км, М
= 90 км, М 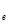 = 90 км.
= 90 км.
15. Рабочие бригады имеют следующий стаж работы на данном предприятии:
| Табельный номер рабочего | 005 | 006 | 007 | 008 | 009 | 014 |
| Стаж работы, лет | 14 | 9 | 11 | 13 | 8 | 2 |
Определите средний стаж работы:
а) 8,2;
б) 9,5;
в) 8,26.
16. Профессиональная психодиагностика дала следующие тестовые оценки:
| Первичные тестовые оценки, баллы | Количество обследованных |
| 15 16 17 18 19 20 | 7 12 21 39 26 15 |
| Итого | 120 |
Определите модальную тестовую оценку:
а) 39; б) 19,5; в) 18,58; г) 18.
17. По данным задания 16 определите медианную тестовую оценку:
а) 18,51; б) 18; в) 17,5; г) 19.
18. Определите среднюю рентабельность предприятий по следующим данным:
| № предприятия | Прибыль, млн. руб. | Рентабельность, % |
| 1 | 250 | 31 |
| 2 | 480 | 25 |
а) 26,8%; б) 28,0%; в) 27,1%.
19. Качество продукции предприятия характеризуется следующими данными (за месяц):
| Вид продукции | Процент брака | Стоимость бракованной продукции, руб. |
| А | 1,3 | 2135 |
| В | 0,9 | 3560 |
| С | 2,4 | 980 |
Определить средний процент брака в целом по предприятию:
а) 1,1%; б)1,5%; в) 1,3%.
20. Определите среднюю окупаемость затрат на развитие новаторских работ по следующим данным:
| Новаторские работы | Доход от использования работ, млн. руб. | Окупаемость 1 млн. затрат на развитие новаторства, млн. руб. |
| Изобретения Рационализаторские предложения | 391 377 | 4,6 6,5 |
а) 5,37; б) 5,53; в) 5,55.
1.7 Статистическое изучение вариации социально-
экономических явлений
1.7.1 Понятие вариации
Вариация – это многообразие, колеблемость, изменяемость величины признака у единиц статистической совокупности. Вариация порождается комплексом условий, действующих на совокупность и ее единицы. Например, вариация доходов, получаемых гражданами, порождается различными социальными и экономическими причинами, однако если бы все граждане имели одинаковые доходы, то необходимость в статистическом исследовании отпала бы. Отсюда следует, что именно вариация и предопределяет необходимость статистики.
Исследование вариации в статистике и социально-экономических исследованиях имеет большое значение, делая возможным установление разброса или вариации значений отдельных единиц совокупности, например, какие факторы и в какой степени влияют на курс акций, объем ВВП, объемы спроса и предложения, процентные ставки, финансовое положение предприятий и т.д. Определение вариации необходимо при организации выборочного наблюдения, построении статистических моделей, разработке материалов экспертных опросов и во многих других случаях.
По степени вариации можно судить о многих сторонах процесса развития изучаемых явлений, в частности об однородности совокупности, устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками одного и того же явления и признаками разных явлений.
Вариация существует во времени и в пространстве. Под вариацией во времени подразумевают изменение значений признака в различные моменты времени (срок службы товаров длительного пользования, средняя продолжительность жизни, мнения людей и т.д.). Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям.
Наличие вариации в признаках изучаемых явлений ставит перед статистикой задачи ее исследования: определение меры вариации, ее измерение, нахождение соответствующих измерителей, показателей, характеризующих ее размеры, выявление их сущности и методов вычисления факторов, ее определяющих.
Статистические показатели, характеризующие вариацию, широко применяются в практической деятельности. На основе показателей вариации в статистике разрабатываются другие показатели и методы изучения явлений и процессов общественной жизни – показатели тесноты связи между явлениями и их признаками, показатели оценки точности выборочного наблюдения и т.д.
1.7.2 Показатели вариации
Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям вариации относятся:
§ размах вариации;
§ среднее линейное отклонение;
§ дисперсия;
§ среднее квадратическое отклонение.
Относительными показателями вариации являются:
§ относительное линейное отклонение;
§ коэффициент вариации и др.
Для иллюстрации расчетов этих показателей воспользуемся следующими данными:
Таблица 1.7.1
Распределение организаций по размерам среднемесячных
затрат на рабочую силу
| Группы организаций по средним размерам затрат на рабочую силу в % от среднеотраслевых затрат | Удельный вес предприятий по обследованным отраслям экономики, в % к итогу |
| до 30 | 13,2 |
| 30 – 50 | 28,6 |
| 50 – 75 | 24,9 |
| 75 – 100 | 13,6 |
| 100 – 150 | 12,2 |
| 150 – 250 | 5,7 |
| 250 – 300 | 1,8 |
| Итого: | 100 |
Самым простым показателем, уже использованным выше при группировке данных, является размах вариации. Он представляет собой разность максимального и минимального значений признака:
R = 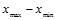 =300 – 0 = 300% (1.7.1)
=300 – 0 = 300% (1.7.1)
Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ. Для анализа вариации необходим и показатель, который отражает все колебания варьирующего признака, дающий обобщенную ее характеристику. В качестве такой величины можно условно принять среднюю величину из всех значений признака, так как в ней более или менее погашаются случайные отклонения от закономерного хода развития явления, и средняя тем самым отражает типичный размер признака у данной однородной совокупности единиц.
Такая средняя называется средним линейным отклонением ( 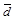 ). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант х
). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант х 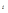 и
и 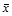 (взвешенная или простая в зависимости от исходных условий) по следующим формулам:
(взвешенная или простая в зависимости от исходных условий) по следующим формулам:
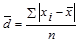 (1.7.2) – простая формула;
(1.7.2) – простая формула;
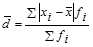 (1.7.3) – взвешенная формула;
(1.7.3) – взвешенная формула;
По данным нашего примера определим среднее линейное отклонение, построив для удобства расчетов вспомогательную табл. 1.7.2.
1) находим середины интервалов ( 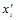 ) по исходным данным (гр. 1) и записываем их в таблицу (гр. 3);
) по исходным данным (гр. 1) и записываем их в таблицу (гр. 3);
2) определим произведения значений середин интервалов ( 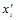 ) на соответствующие им веса (f
) на соответствующие им веса (f  ) (гр. 4). В итоге получаем 7248,3. Рассчитаем среднюю величину по формуле средней арифметической взвешенной:
) (гр. 4). В итоге получаем 7248,3. Рассчитаем среднюю величину по формуле средней арифметической взвешенной:
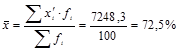
Таблица 1.7.2
Распределение организаций по размерам среднемесячных
затрат на рабочую силу
Группы организаций
по средним размерам
затрат
на рабочую
силу в % от
средне-отраслевых
затрат
х 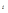
| Удельный вес предприя-тий по обследо-ванным
отраслям
экономики,
в % к итогу
f 
| Сере-
дина
ин-
тер-
вала
( 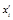 ) )
|
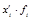
|
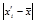
|
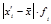
|
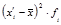
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| до 30 | 13,2 | 15,0 | 198,0 | 57,5 | 759 | 43642,5 |
| 30 – 50 | 28,6 | 40,0 | 1144,0 | 32,5 | 929,5 | 30208,75 |
| 50 – 75 | 24,9 | 62,5 | 1556,3 | 10 | 249 | 2490 |
| 75 – 100 | 13,6 | 87,5 | 1190,0 | 15 | 204 | 3060 |
| 100 – 150 | 12,2 | 125 | 1525,0 | 52,5 | 640,5 | 33626,25 |
| 150 – 250 | 5,7 | 200 | 1140,0 | 127,5 | 726,75 | 92660,63 |
| 250 – 300 | 1,8 | 275 | 495,0 | 202,5 | 364,5 | 73811,25 |
| Итого: | 100 | 7248,3 | 3873,25 | 279499,38 |
3) для расчета среднего линейного отклонения находим абсолютные отклонения середины интервалов, принятых нами в качестве вариантов признака ( 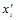 ) от средней величины (
) от средней величины ( 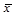 ) (гр. 5)
) (гр. 5)
4) вычисляем произведения отклонений | 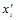 -
- 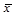 | на их веса (f
| на их веса (f  ) и подсчитываем сумму этих произведений (3873,25). Результаты заносим в гр. 6.
) и подсчитываем сумму этих произведений (3873,25). Результаты заносим в гр. 6.
5) делим эту сумму на сумму весов, чтобы получить искомую величину 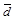 :
:
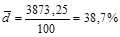
Следующие абсолютные показатели, которые мы будем определять, это дисперсия и среднее квадратическое отклонение. Эти показатели являются общепринятыми мерами вариации и часто используются в статистических исследованиях.
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
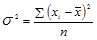 (1.7.4) – простая формула;
(1.7.4) – простая формула;
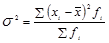 (1.7.5) – взвешенная формула;
(1.7.5) – взвешенная формула;
Среднее квадратическое отклонение определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак:
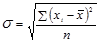 (1.7.6) – простая формула;
(1.7.6) – простая формула;
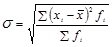 (1.7.7) – взвешенная формула;
(1.7.7) – взвешенная формула;
Рассмотрим расчет дисперсии и среднего квадратического отклонения по данным таблицы 1.7.2.
1) возводим отклонения 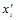 от
от 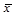 во вторую степень и умножаем на их веса f
во вторую степень и умножаем на их веса f  , затем подсчитываем сумму этих произведений. Эта сумма равна 279499,38. Результаты записываем в гр. 7.
, затем подсчитываем сумму этих произведений. Эта сумма равна 279499,38. Результаты записываем в гр. 7.
2) разделив эту сумму на сумму весов, получаем дисперсию:
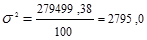
3) извлекая из дисперсии корень второй степени, получаем среднее квадратическое отклонение:
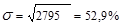
Степень вариации в данной совокупности велика, так как средняя величина равна 72,5%. Это говорит о том, что рассматриваемая нами совокупность неоднородна.
Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них, относительное линейное отклонение и коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня, что во многих случаях является предпочтительнее.
Относительное линейное отклонение ( 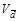 ):
):
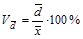 (1.7.8)
(1.7.8)
Определим значение этого показателя по нашим данным:
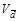 =38,7/ 72,5*100=53,4%
=38,7/ 72,5*100=53,4%
Коэффициент вариации ( 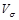 ):
):
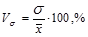 (1.7.9)
(1.7.9)
Определим значение коэффициента вариации по нашим данным:
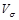 =52,9/ 72,5*100=73,0%
=52,9/ 72,5*100=73,0%
Рассчитанная величина свидетельствует о значительном относительном уровне колеблемости признака. Если 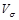 превышает 33%, то совокупность по рассматриваемому признаку можно считать неоднородной.
превышает 33%, то совокупность по рассматриваемому признаку можно считать неоднородной.
Следует отметить, что дисперсию используют не только для оценки вариации, но и при измерении взаимосвязей, для проверки статистических гипотез и т.п.
Дисперсия может быть рассчитана и по упрощенной формуле:
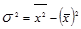 (1.7.10)
(1.7.10)
Как и любая средняя, дисперсия имеет определенные математические свойства:
а) если все значения признака х 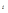 уменьшить (увеличить) на определенную величину, дисперсия не изменится;
уменьшить (увеличить) на определенную величину, дисперсия не изменится;
б) если все значения признака изменить в k раз, то дисперсия изменится в k 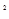 раз;
раз;
в) в случае замены частот частостями дисперсия не изменится.
Статистическое изучение вариации многих социально-экономических явлений проводится и при помощи дисперсии альтернативного признака, вариация которого имеет два взаимоисключающих значения – «1» (наличие данного признака) и «0» (отсутствие его), долю вариантов, обладающих данным признаком, р, и не обладающих им q. Так как ряд р + q = 1, то средняя 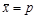 , а дисперсия альтернативного признака
, а дисперсия альтернативного признака 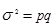 , где
, где 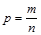 , n – число наблюдений, m – число единиц совокупности, обладающее данным признаком, q = 1- р. Отсюда дисперсию доли альтернативного признака можно выразить следующим образом:
, n – число наблюдений, m – число единиц совокупности, обладающее данным признаком, q = 1- р. Отсюда дисперсию доли альтернативного признака можно выразить следующим образом:
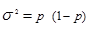 (1.7.11)
(1.7.11)
Пример. Экзамен по информатике сдали 25 человек из 30. Определим дисперсию доли студентов, не сдавших экзамен:
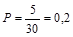
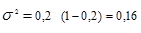
Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.
1.7.3 Виды дисперсий и методы их расчета
Для совокупности, сгруппированной по определенному признаку можно рассчитать три вида дисперсий:
§ внутригрупповую дисперсию;
§ межгрупповую дисперсию;
§ общую дисперсию.
Внутригрупповая дисперсия оценивает колеблемость значения индивидуального признака внутри группы. Эта вариация возникает под влиянием неучтенных факторов и не зависит от признака, положенного в основу группировки. Она исчисляется следующим образом:
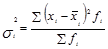 , (1.7.12)
, (1.7.12)
где 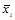 - средняя по изучаемой группе (групповая средняя).
- средняя по изучаемой группе (групповая средняя).
Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Средняя из внутригрупповых дисперсий определяется по формуле арифметической взвешенной:
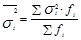 (1.7.13)
(1.7.13)
Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием признака факторного. Это воздействие проявляется в отклонении групповых средних от общей средней:
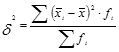 (1.7.14)
(1.7.14)
Общая дисперсия оценивает вариацию изучаемого признака, возникающего под влиянием всех факторов.
Между рассматриваемыми видами дисперсий существует определенная взаимосвязь, которая называется правилом сложения дисперсий:
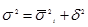 (1.7.15)
(1.7.15)
Согласно правилу сложения дисперсий общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.
Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.
На основании правила сложения дисперсий можно измерить тесноту связи между группировочным (факторным) и результативным признаками. Для этого рассчитывается:
1) коэффициент детерминации:
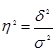 (1.7.16)
(1.7.16)
Коэффициент детерминации показывает, какая доля вариации результативного признака объясняется вариацией признака фактора, положенного в основу группировки.
2) эмпирическое корреляционное отношение:
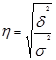 (1.7.17)
(1.7.17)
Величина показателя изменяется в пределах от 0 до 1. Чем ближе к 1, тем сильнее взаимосвязь между рассматриваемыми признаками.
Пример: По данным обследования коммерческих банков города, 70% общего числа клиентов составили юридические лица со средним размером кредита 120 тыс. руб. и коэффициентом вариации 25%, а 30% - физические лица со средним размером ссуды 20 тыс. руб. при среднем квадратическом отклонении 6 тыс. руб.
Используя правила сложения дисперсий, определим тесноту связи между размером кредита и типом клиента, исчислив эмпирическое корреляционное отношение.
Расчет эмпирического корреляционного отношения включает несколько этапов:
1) в данном примере групповые средние нам даны по условию:
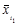 = 120 тыс. руб.;
= 120 тыс. руб.; 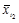 = 20 тыс. руб.;
= 20 тыс. руб.;
2) рассчитаем, используя групповые средние, общую среднюю:
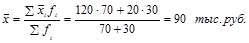
3) затем вычислим среднюю из внутригрупповых дисперсий. Для этого сначала проведем расчеты дисперсий по группам, используя исходные данные:
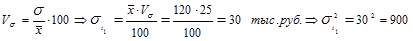 ;
;
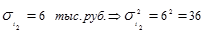 ;
;
Подставив полученные значения в формулу, получим:
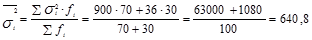
4) теперь определим межгрупповую дисперсию:
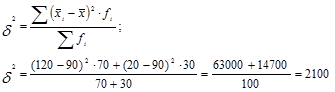
Таким образом, общая дисперсия по правилу сложения дисперсий равна:
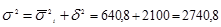
5) рассчитаем эмпирическое корреляционное отношение:
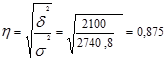
Полученная величина свидетельствует о том, что тип клиента существенно влияет на размер кредита.
Наряду с вариацией индивидуальных значений признака вокруг средней может наблюдаться и вариация индивидуальных долей признака вокруг средней доли. Для анализа этой вариации вычисляются следующие виды дисперсий.
Внутригрупповая дисперсия доли определяется по следующей формуле:
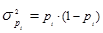 (1.7.18)
(1.7.18)
Средняя из внутригрупповых дисперсий:
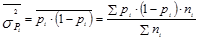 (1.7.19)
(1.7.19)
Межгрупповая дисперсия:
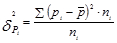 , (1.7.20)
, (1.7.20)
где 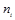 - численность единиц в отдельных группах;
- численность единиц в отдельных группах;
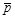 - доля изучаемого признака во всей совокупности, которая определяется по следующей формуле:
- доля изучаемого признака во всей совокупности, которая определяется по следующей формуле:
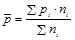 (1.7.21)
(1.7.21)
Общая дисперсия имеет вид:
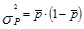 (1.7.22)
(1.7.22)
Три вида дисперсии связаны между собой следующим образом:
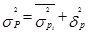 (1.7.23)
(1.7.23)
Данная взаимосвязь дисперсий называется теоремой сложения дисперсии доли признака. Эта теорема широко используется в изучении колеблемости качественных признаков.
Тренировочные задания
1. Имеются следующие выборочные данные о расходах на платные услуги домохозяйствами городского и сельского населения:
| Группы населения | Обследовано домохозяйств | Доля расходов на платные услуги, % |
| Городское | 620 | 40 |
| Сельское | 280 | 30 |
Определите для домохозяйств городского и сельского населения:
1) общую дисперсию;
2) среднюю из групповых дисперсий;
3) межгрупповую дисперсию, используя правило сложения дисперсий.
Решение:
1. Определим общую дисперсию. Для этого сначала рассчитаем долю изучаемого признака во всей совокупности:
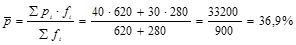 ,
,
Подставив полученное значение в формулу, получим:
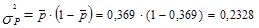 ;
;
2. Вычислим среднюю из групповых дисперсий:
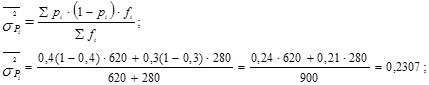
3. Теперь рассчитаем межгрупповую дисперсию, используя правило сложения дисперсий:
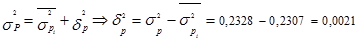 ;
;
Проверим полученный результат, исчислив межгрупповую дисперсию обычным способом:
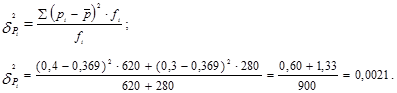
2. Инспекционная проверка качества твердых сыров сорта X на содержание в них жира дала следующие результаты:
| Содержание жира, % | 44 | 45 | 46 | 47 | 48 | Итого |
| Количество проб | 1 | 5 | 9 | 3 | 2 | 20 |
Определите средний процент содержания жира в твердых сырах и среднее линейное отклонение.
3. Имеются следующие выборочные данные о вкладах населения района:
| Группы населения | Число вкладов, ед. | Средний размер вклада, тыс. руб. | Коэффициент вариации вклада, % |
| Городское | 3500 | 32 | 20 |
| Сельское | 1500 | 18 | 30 |
Определите тесноту связи между средним размером вклада и типом населения, исчислив эмпирическое корреляционное отношение.
4. Определите среднюю длину пробега такси и вычислите все показатели вариации, если известны:
| Длина пробега за один рейс, км | Число рейсов за месяц |
| до 2 2 – 5 5 – 10 10 – 15 свыше 15 | 20 25 14 5 3 |
| Всего | 67 |
5. Средний квадрат индивидуальных значений признака равен 930, а его дисперсия – 700. Определить величину средней.
6. Определить среднюю величину, если известно, что коэффициент вариации равен 20%, а дисперсия признака – 650.
7. Имеются следующие данные о распределении сотрудников компании по среднемесячной заработной плате:
| Группы сотрудников по среднемесячной ЗП, тыс. руб. | до 5 | 5 – 7 | 7 – 9 | 9 – 11 | 11 – 12 | 12 – 15 | свыше 15 | Итого |
| Количество сотрудников, чел. | 35 | 30 | 23 | 20 | 11 | 9 | 7 | 135 |
 Определите общую дисперсию двумя способами:
Определите общую дисперсию двумя способами:
а) обычным; б) по формуле 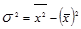 .
.
8. На конец года текущие коэффициенты ликвидности предприятий-заемщиков составляли:
| Коэффициент ликвидности | до 1,5 | 1,5 – 1,7 | 1,7 – 1,9 | 1,9 – 2,1 | 2,1 и выше | Итого |
| Доля предприятий, % | 5 | 10 | 20 | 45 | 20 | 100 |
Определите среднюю, моду и показатели вариации. Сделайте вывод о характере распределения предприятий-заемщиков по уровню ликвидности.
9. По результатам проверки сахаристость свеклы характеризуется следующими данными:
| Сахаристость, % | 12 - 14 | 14 - 16 | 16 - 18 | 18 и выше | Итого |
| Количество проб | 1 | 4 | 3 | 2 | 10 |
Определите средний уровень и дисперсию сахаристости свеклы, долю проб сахарной свеклы с наивысшей сахаристостью и дисперсию этой доли.
10. Исчислить дисперсию, если известно, что средняя величина признака равна 250 руб., а коэффициент вариации – 30%.
11. По данным обследований домохозяйств, общая площадь в расчете на одного члена домохозяйства составляла, м 2:
| Общая площадь на одного члена домохозяйства, м2 | до 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 и более | Итого |
| Число домохозяйств | 42 | 54 | 47 | 37 | 20 | 200 |
Определите характеристики распределения: среднюю, медиану, среднее квадратическое отклонение, коэффициент вариации. Сделайте вывод о характере распределения домохозяйств по уровню обеспеченности жильем.
Тест
1. Дисперсия - это:
а) средний модуль отклонений индивидуальных значений признака от средней;
б) средний квадрат этих отклонений;
в) сумма квадратов отклонений индивидуальных значений признака от средней.
2. Какой из показателей вариации характеризует абсолютный размер колеблемости признака около средней величины?
а) коэффициент вариации;
б) дисперсия;
в) коэффициент осцилляции;
г) относительное линейное отклонение.
3. Средние значения признака в двух совокупностях одинаковы. Может ли быть разной вариация в этих совокупностях?
а) да;
б) нет.
4. Средние значения признака в двух совокупностях разные. Может ли быть одинаковой вариация признака в этих совокупностях?
а) да;
б) нет.
5. Какой из показателей вариации характеризует относительный размер колеблемости признака около средней величины?
а) квартильное отклонение;
б) дисперсия;
в) размах вариации;
г) среднее квадратическое отклонение;
д) относительное линейное отклонение.
6. Если все значения признака увеличить на определенную величину, то дисперсия:
а) увеличится на такую же величину;
б) уменьшится на такую же величину;
в) не изменится;
г) предсказать изменение дисперсии невозможно.
7. Если все значения признака увеличить в k раз, то дисперсия:
а) увеличится в k раз;
б) уменьшится в k раз;
в) увеличится в k 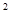 раз;
раз;
г) уменьшится в k 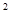 раз;
раз;
8. Выберите правильную взвешенную формулу дисперсии:
а) 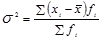 ; б)
; б) 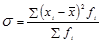 ;
;
в) 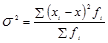 ; г)
; г) 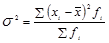 ;
;
д) 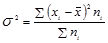 .
.
9. Средний модуль отклонений индивидуальных значений признака от средней величины называют:
а) дисперсией;
б) средним линейным отклонением;
в) линейным коэффициентом вариации;
г) размахом вариации.
10. Правило сложения дисперсий состоит в том, что:
а) общая дисперсия равна сумме групповых дисперсий;
б) общая дисперсия равна сумме межгрупповой и средней из групповых дисперсий;
в) межгрупповая дисперсия равна сумме групповых дисперсий;
г) средняя из групповых дисперсий равна сумме межгрупповой и общей дисперсий.
11. В каких пределах изменяется эмпирическое корреляционное отношение?
а) [0; µ]; б) [1; 0]; в) [0; 1]; г) [µ;0].
12. Средняя выработка рабочих цеха составляет 12 деталей/час. Определите среднее квадратическое отклонение выработки при условии, что средний квадрат равен 160.
а) 12; б) 148;
в) 16; г) 4.
13. Определить среднюю величину, если известно, что коэффициент вариации равен 30%, а дисперсия признака – 800.
а) 36,67; б) 94,3;
в) 26,67; г) 2666,67.
14. При производстве 450 изделий А израсходовано 1350 кг материала В. Определите среднее квадратическое отклонение расхода материала В на единицу изделия А при условии, что сумма квадратов равна 8100.
а) 3; б) 4;
в) 9; г) 15.
15. Налоговой инспекцией одного из районов города проверено 86 коммерческих киосков, в 37 обнаружены финансовые нарушения. Определите дисперсию доли коммерческих киосков, имеющих финансовые нарушения.
а) 0,43;
б) 0,57;
в) 0,245.
16. Средние расходы домохозяйств в расчете на одну потребительскую единицу составляли, руб. в месяц: на питание – 520 при среднем квадратическом отклонении 60; на коммунальные услуги – 240 при среднем квадратическом отклонении 60. Степень вариации расходов на питание и коммунальные услуги:
а) одинакова;
б) вариация расходов на питание больше;
в) вариация расходов на питание .меньше;
г) сравнить вариацию невозможно.
17. По данным статистики 60% новообразованных предприятий малого бизнеса прекращают свою деятельность в течение первых двух лет. Определите дисперсию доли таких МП:
а) 0,60;
б) 0,40;
в) 0,24;
г) 0,76.
18. Экзамен по информатике сдали 25 человек из 30. Определить дисперсию доли студентов сдавших экзамен:
а) 0,141;
б) 0,125;
в) 0,160;
г) 0,175.
19. Определите коэффициент вариации, если известно, что средняя равна 100, а дисперсия 64.
а) 36%;
б) 64%;
в) 8%;
г) 5%.
20. Определите дисперсию, если известно, что средняя величина равна 40, а средний квадрат значения признака 2500.
а) 2540; б) 2460;
в) 4100; г) 900.








