Для дискретных рядов распределения мода – это варианта с наибольшей частотой.

Дата: 2025-05-25; Просмотры: 5
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Пример 2. Распределение торговых фирм города по уровню оптовых цен на товар «Х» имеет следующий вид:

 

Цена, долл. США 22 23 24 25 26 Итого
Число торговых фирм 13 49 57 61 15 195
Сумма накопленных частот, S 13 62 119 180 195  

 

Это дискретный вариационный ряд, т.к. признак (цена) изменяется прерывно, то есть через определенное число единиц, в данном случае через единицу. Наибольшую частоту – 61 - имеет цена 25 долл. США, следовательно, она и является модальной.

Для интервальных вариационных рядов распределения мода рассчитывается по следующей формуле:

 

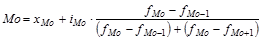, (1.6.5)

 

где Мо – мода;

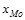- нижняя граница модального интервала;

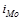- величина модального интервала;

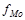- частота модального интервала;

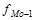- частота интервала, предшествующего модальному интервалу;

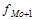- частота интервала, следующего за модальным интервалом.

Пример 3. Имеются следующие данные о распределении работников предприятия по уровню среднемесячной заработной платы:

 

Заработная плата, долл. США х 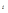Число работников, чел. f Сумма накопленных частот S
До 600 600 – 700 700 – 800 800 – 900 900 – 1000 Свыше 1000 20 40 80 70 35 15 20 60 140 210 245 260
Итого 260  

 

Первоначально определим по наибольшей частоте признака модальный интервал. Наибольшее число работников – 80 человек – имеют заработную плату в интервале 700 – 800 долл. США, который и является модальным.

 

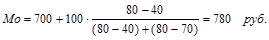
Медиана – это значение изучаемого признака, расположенного в середине ранжированного ряда распределения.

Ранжированный ряд – ряд, расположенный в порядке возрастания или убывания значений признака.

Для определения медианы сначала определяют ее место в ряду, используя формулу:

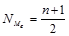, (1.6.6)

где n – число членов ряда

 

 

Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую из двух вариантов, расположенных в середине ряда.

 

В примере 1 для определения медианы производится ранжирование данных.

 

Ранжированный ряд: 1300; 1300; 1300; 1330; 1350; 1370; 1380; 1450;1470.

Место медианы - .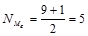

Ме = 1350 ч (1350 – значение признака, находящиеся на 5-ом месте в ранжированном ряду).