Таким образом, условиями применения средних величин являются: наличие качественно однородной совокупности и достаточно большой ее объем.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.
На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:
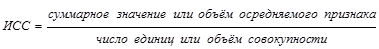 (1.6.1)
(1.6.1)
Так, например, для расчета средней себестоимости единицы продукции необходимо общие затраты на выпуск продукции разделить на количество выработанной продукции:
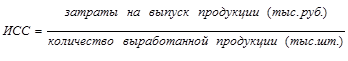
Числитель исходного соотношения средней представляет собой ее определяющий показатель. Для средней себестоимости единицы продукции таким определяющим показателем являются на выпуск продукции. Независимо от того, какой первичной информацией мы располагаем - известны ли нам общие затраты на выпуск продукции или средняя себестоимость единицы продукции и количество выработанной продукции или какие-либо другие исходные данные - в любом случае среднюю себестоимость единицы продукции можно получить только через данное исходное соотношение средней.
Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней.
Если, например, требуется рассчитать среднюю процентную ставку по кредиту, то исходное соотношение будет следующим:
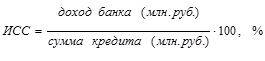
Если же необходимо определить средний размер вклада в банке, то потребуется следующее исходное соотношение:
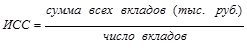
Поэтому, каким именно образом будет реализовано исходное соотношение средней, зависит от того, в каком виде представлены исходные данные для ее расчета.
1.6.2 Виды средних и способы их вычисления
В экономических исследованиях и плановых расчетах применяются два класса средних:
§ степенные средние;
§ структурные средние.
К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, кубическая и т.д. Величины, для которых исчисляется средняя, обозначаются буквой х 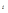 . Средняя обозначается через
. Средняя обозначается через 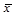 . Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта сверху символизирует процесс осреднения индивидуальных значений. Частота – повторяемость индивидуальных значений признака – обозначается буквой f .
. Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта сверху символизирует процесс осреднения индивидуальных значений. Частота – повторяемость индивидуальных значений признака – обозначается буквой f .
Формулы средних величин могут быть получены на основе степенной средней, для которой определяющей функцией является уравнение:
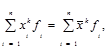 (1.6.2)
(1.6.2)
откуда
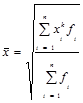 (1.6.3)
(1.6.3)
В дальнейшем при написании формул средних подстрочные значки i , n использоваться не будут, но подразумевается, что суммируются все произведения 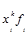 .
.
В зависимости от того, какое значение приобретает показатель степени k, получают различные виды средних величин, их формулы представлены в таблице 1.6.1.
Как видно из данных табл. 1.6.1, взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, то есть умножают на нее. Частоты f при этом называются статистическими весами или просто весами средней.
Однако необходимо учитывать, что статистический вес – понятие более широкое, чем частота. В качестве веса могут применяться какие-либо другие величины (в табл. 1.6.1 они обозначены буквой w). Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными – частостями.
Таблица 1.6.1
Формулы различных видов степенных средних величин
| Зна- чение k | Наименование средней | Формула средней величины | |
| простая | взвешенная | ||
| -1 | Гармоническая | 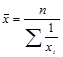
| 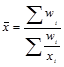
|
| 0 | Геометрическая | 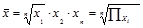
| 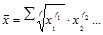
|
| 1 | Арифметическая | 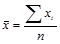
| 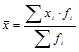
|
| 2 | Квадратическая | 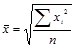
| 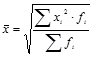
|
Наиболее распространенным видом средних величин является средняя арифметическая. Средняя арифметическая простая (невзвешенная) используется в тех случаях, когда расчет осуществляется по несгруппированным данным.
Пример: уставный капитал сформирован 7 учредителями акционерной компании, размер взноса каждого из них составляет, млн. ден. ед.: 7, 12, 4, 6, 10, 9, 8. Средний взнос одного учредителя составил (см. табл. 1.6.1):
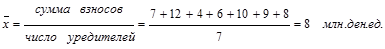
По формуле средней арифметической простой вычисляются также средние в хронологическом ряду, если интервалы времени, за которые приводятся значения признаков, равны.
При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.
Пример: по результатам сдачи экзамена по дисциплине «Рынок ценных бумаг» студентами группы ЭК – 31 получены следующие данные:
Таблица 1.6.2
Результаты сдачи экзамена по дисциплине
«Рынок ценных бумаг»
| Оценка знаний студентов, балл | х 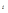
| 5 | 4 | 3 | 2 | Итого |
| Количество оценок | f 
| 10 | 12 | 5 | 3 | 30 |
Определим по данному дискретному вариационному ряду средний балл оценок, что можно сделать только, используя формулу средней арифметической взвешенной (см. табл. 1.6.1):
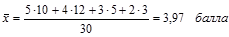
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы).
Так, в приведенном выше примере доля оценок соответственно составляет 33,3% (0,333); 40,0% (0,400); 16,7% (0,167) и 10,0% (0,100) от их общего количества. Тогда, с учетом несложного преобразования формулы средневзвешенной арифметической получим:
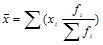 (1.6.4)
(1.6.4)
или
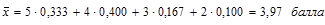
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам. Рассмотрим следующий пример:
Таблица 1.6.3
Распределение скважин в одном из районов
бурения по глубине
| Группы скважин по глубине, м | Число скважин |
| До 500 500 - 1000 1000 - 1500 1500 - 2000 Свыше 2000 | 4 9 17 8 2 |
| Итого | 40 |
Для определения средней глубины скважин найдем середины интервалов скважин. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам интервалов, примыкающих к ним (второго и предпоследнего). С учетом этого середины интервалов будут следующими:
| 250 | 750 | 1250 | 1750 | 2250 |
Используя среднюю арифметическую взвешенную (см. табл. 1.6.1), определим среднюю глубину скважин в одном из районов бурения:
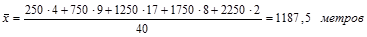
Средняя арифметическая имеет определенные математические свойства, более полно раскрывающие ее сущность. Так, сумма отклонений отдельных вариант от средней равна нулю, а сумма квадратов таких отклонений приближается к минимуму. Эти два свойства лежат в основе изучения вариации признаков.
Если отдельные значения вариант увеличить (уменьшить) на величину А или в k раз, то средняя изменится соответственно.
Например, если денежные вклады граждан в Сбербанк скорректировать на уровень инфляции, составляющий 1,3, то средний размер вклада увеличится соответственно в 1,3 раза.
Средняя не изменится при пропорциональном изменении всех весов, но ее размер изменится, если произойдут структурные сдвиги.
Например, при неизменной курсовой стоимости акций отдельных эмитентов средняя стоимость акций может увеличиться за счет увеличения доли «дорогих» акций в общем количестве их продажи.
Средняя гармоническая используется для осреднения индивидуальных значений признаков из обратных величин путем их суммирования.
Для несгруппированных данных используется средняя гармоническая простая, если данные сгруппированы, то используют среднюю гармоническую взвешенную (см. табл. 1.6.1).
Пример: рассмотрим расчет средней прибыли на одну акцию по двум фирмам за отчетный период по сгруппированным данным, представленным в табл. 1.6.4:
Таблица 1.6.4
Финансовые показатели фирм
| № фирмы | Прибыль на одну акцию, руб. | Сумма прибыли, тыс. руб. |
| 1 | 9,0 | 810 |
| 2 | 8,0 | 480 |
Средняя прибыль на одну акцию может быть определена только на основе следующего исходного соотношения:
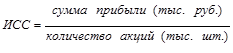
Сумму прибыли мы получим простым суммированием суммы прибыли по фирмам. Данные же о количестве акций отсутствуют, но их можно получить, разделив сумму прибыли по каждой фирме на прибыль на одну акцию. С учетом этого определим искомую среднюю по формуле среднегармонической взвешенной (см. табл. 1.6.1):
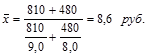
Таким образом, средняя прибыль на одну акцию за отчетный период по двум фирмам составляла 8,6 руб.
Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов.
Средняя геометрическая наиболее широкое применение получила в анализе динамики для определения среднего темпа роста.
Пример: Количество зарегистрированных преступлений за четыре года возросло в 1,73 раза, в том числе за первый год – в 1,18, за второй – в 1,12, за третий – в 1,16, за четвертый – в 1,13 раза. Среднегодовой темп роста количества зарегистрированных преступлений составляет:
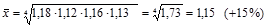
Таким образом, число зарегистрированных преступлений ежегодно возрастало в среднем на 15%.
Если временные интервалы неодинаковы, используют среднюю геометрическую взвешенную (см. табл. 1.6.1).
Средняя квадратическая лежит в основе вычислений ряда сводных расчетных показателей. Наиболее широко этот вид средней используется при расчете показателей вариации, что будет рассмотрено в соответствующей главе.
В статистическом анализе также применяются степенные средние 3-го порядка и более высоких порядков.
1.6.3 Структурные средние
В отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, структурные средние выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.
Наиболее часто используемыми в экономической практике структурными средними являются:
§ мода;
§ медиана.
Мода – значение изучаемого признака чаще всего встречающееся в ряду распределения.
Пример 1. Проведена малая выборка из партии электрических лампочек для определения продолжительности их службы. Получены следующие результаты:
| № лампочки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Срок горения, час. | 1350 | 1300 | 1470 | 1330 | 1300 | 1380 | 1370 | 1450 | 1300 |
Мода (Мо) будет равна 1300 часов, так как 1300 – значение признака, встречающиеся чаще всего (три раза) в ряду распределения.








