Возведение в квадрат суммы и разности двух выражений.
23. 12. 2022 г. 7 класс. Алгебра.
Возведение в квадрат суммы и разности двух выражений.
Цели и задачи урока: познакомиться с формулами квадрата разности и квадрата суммы.
В прошлый раз мы с вами познакомились с первой формулой сокращённого умножения, с формулой разности квадратов. Сегодня мы поговорим ещё о двух формулах, это формулы квадрат суммы и квадрат разности.
Рассмотрим выражение
(a + b)2
Сразу ясно, что такое квадрат суммы. Взяли сумму и возвели её в квадрат. Распишем данный квадрат и выполним раскрытие скобок, после чего приведём подобные слагаемые.
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
Если убрать преобразования, то имеем:
(a + b)2 = a2 + 2ab + b2
Эта формула и называется формулой квадрата суммы. Т. е. квадрат суммы двух слагаемых равен квадрату первого слагаемого плюс удвоенное произведение первого на второе слагаемое плюс квадрат второго слагаемого.
Теперь перейдём к квадрату разности. Опять же, следуя из названия, есть некая разность, и она возводится в квадрат
(a – b)2 = (a – b)(a – b) = a2 – ab – ab + b2 = a2 – 2ab + b2
(a – b)2 = a2 – 2ab + b2
Эта формула называется формулой квадрата разности.
Кстати, эту формулу можно доказать иначе:
(a +(–b))2 = (a +(–b))(a + (–b)) = a2 + a(–b) + a(–b) + b2 = a2 + 2a(–b) + b2 = a2 – 2ab + b2
Где же применяются формулы квадрат суммы и квадрат разности?
Пример 1:
Вычислить 912
912 = (90 + 1)2 = 902 + 2 ⋅ 90 ⋅ 1 + 12 = 8100 + 180 + 1 = 8281
Пример 2:
Вычислить 782
782 = (80 – 2)2 = 802 – 2 ⋅ 80 ⋅ 2 + 22 = 6400 – 320 + 4 = 6084
Пример 3:
Применяем формулу квадрат суммы.
(a + 2b)2 = a2 + 2a2b + (2b)2= a2 + 4ab + 4b2
Пример 4:
(2a – 5b)2 = (2a)2 – 2 ⋅ 2a ⋅ 5b + (5b)2= 4a2 – 20ab +25b2
Пример 5:
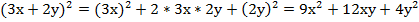 .
.
Комментарий: пример решен с применением формулы квадрата суммы.
Пример 6:
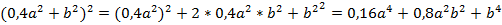 .
.
Пример 7:
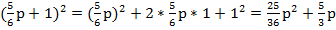 +1.
+1.








