3. Информация, располагаемая в столбцах (графах) таблицы должна завершаться итоговой строкой.
4. Графы и строки полезно нумеровать.
5. Если названия отдельных граф повторяются между собой, содержат повторяющиеся термины или несут единую смысловую нагрузку, то необходимо им присвоить объединяющий заголовок.
6. Числа целесообразнее, по возможности, округлять. Округление чисел в пределах одной и той же графы или строки следует проводить с одинаковой степенью точности (до целого знака или до десятого и так далее). Если все числа одной и той же графы или строки даны с одним десятичным знаком, а одно из чисел имеет точно два знака после запятой, то числа с одним знаком после запятой следует дополнять нулем, тем самым, подчеркнув их одинаковую точность.
7. Взаимосвязанные данные, характеризующие одну из сторон анализируемого явления (например, число предприятий и удельный вес заводов (в % к итогу) и т.д.), целесообразно располагать в соседних друг с другом графах.
8. Отсутствие данных об анализируемом социально-экономическом явлении может быть обусловлено различными причинами, и это по-разному отмечается:
а) если данная позиция (на пересечении соответствующих графы и строки) вообще не подлежит заполнению, то ставится знак «Х»;
б) если по какой-либо причине отсутствуют сведения, то ставится многоточие «...» или «нет свед.»;
в) если отсутствует явление, то клетка заполняется тире (-). Для отображения очень малых чисел используют обозначения (0,0) или (0,00).
9. Графы и строки должны содержать единицы измерения, соответствующие поставленным в подлежащем и сказуемом показателям. При этом используются общепринятые сокращения единиц измерения (чел., руб., кВт-ч и так далее).
10. В случае необходимости дополнительной информации к таблице могут даваться примечания.
Тренировочные задания
1. Имеются следующие данные о распределении числа вкладчиков по двум коммерческим банкам (данные условные).
| № груп- пы | Банк «А» | Банк «Б» | ||
| Группы вкладчиков по величине вкладов, руб. | Удельный вес, % к итогу | Группы вкладчиков по величине вкладов, руб. | Удельный вес, % к итогу | |
| 1 | до 100 | 3 | до 300 | 5 |
| 2 | 100 - 300 | 10 | 300 - 1500 | 35 |
| 3 | 300 - 500 | 12 | 1500 - 2000 | 6 |
| 4 | 500 - 1000 | 15 | 2000 - 4000 | 24 |
| 5 | 1000 - 3000 | 18 | 4000 - 6000 | 8 |
| 6 | 3000 - 5000 | 25 | 6000 - 20000 | 17 |
| 7 | 5000 - 10000 | 8 | 20000 - 50000 | 3 |
| 8 | 10000 - 30000 | 2 | 50000 и более | 2 |
| 9 10 | 30000 - 50000 50000 и более | 3 4 | ||
| Итого: | 100 | Итого: | 100 | |
Постройте вторичную группировку данных о распределении вкладчиков по величине вклада банка «А» в соответствии с группировкой банка «Б».
Решение:
В первую группу (до 300) входит полностью первая и вторая группы банка «А». Таким образом, получаем:
3+10=13%
Вторую группу (300 - 1500) образуют вкладчики полностью третьей, четвёртой группы банка «А» и часть пятой. Для того чтобы образовать группу до 1500 человек, необходимо от интервала пятой группы взять 1/4. Таким образом, получаем:
12+15+1/4 *18=31,5%
Третью группу (1500 - 2000) составляет также 1/4 часть интервала пятой группы:
1/4*18=4,5%
Четвертую группу (2000 - 4000) составляют оставшаяся 1/2 часть вкладчиков пятой группы и 1/2 часть вкладчиков шестой группы. Отсюда, получаем:
1/2*18+1/2*25=21,5%
Пятую группу (4000 - 6000) составляют оставшаяся 1/2 часть шестой группы и 1/5 часть седьмой группы:
1/2*25+1/5*8=14,1%
Шестую группу (6000-20000) образуют вкладчики оставшейся седьмой группы и 1/5 часть от восьмой группы:
4/5*8+1/4*5=7,65%
Во вновь образуемую седьмую группу (20000 - 50000) войдет вся восьмая группа, за исключением 1/4 её части, то есть 3/4:
3/4*5=3,75%
Восьмая группа новой группировки совпадает с девятой группой предыдущей. Таким образом, получаем 4%.
Результаты вторичной группировки представлены в следующей таблице:
| № груп- пы | Группы вкладчиков по величине вкладов, руб. | Удельный вес, % к итогу |
| 1 | до 300 | 13,0 |
| 2 | 300 - 1500 | 31,5 |
| 3 | 1500 - 2000 | 4,5 |
| 4 | 4000 - 6000 | 14,1 |
| 5 | 6000 - 20000 | 7,65 |
| 6 | 20000 - 50000 | 3,75 |
| 7 | 50000 и более | 4,0 |
| Итого: | 100,0 | |
2. Пользуясь формулой Стерджесса, определите интервал группировки сотрудников фирмы по уровню доходов, если общая численность сотрудников составляет 150 человек, а минимальный и максимальный доход, соответственно, равен 3 000 и 25 000 руб.
Решение:
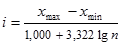
Подставляем в формулу исходные данные и получаем:
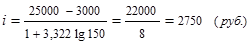
Таким образом, интервал группировки сотрудников фирмы по уровню доходов составляет 2 750 руб.
3. Известны следующие данные по Центральному федеральному округу о потреблении овощей и продовольственных бахчевых культур на душу населения в 2003 г.:
| № п/ п | Центральный федеральный округ | Потребление овощей и продовольственных бахчевых культур, (в год; кг) |
| 1 | Белгородская | 100 |
| 2 | Брянская | 99 |
| 3 | Владимирская | 111 |
| 4 | Воронежская | 101 |
| 5 | Ивановская | 76 |
| 6 | Калужская | 105 |
| 7 | Костромская | 153 |
| 8 | Курская | 111 |
| 9 | Липецкая | 98 |
| 10 | Московская | 78 |
| 11 | Орловская | 94 |
| 12 | Рязанская | 100 |
| 13 | Смоленская | 102 |
| 14 | Тамбовская | 124 |
| 15 | Тверская | 122 |
| 16 | Тульская | 103 |
| 17 | Ярославская | 134 |
| 18 | г. Москва | 64 |
// Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 442
Построить группировку по Центральному федеральному округу по величине потребления овощей и продовольственных бахчевых культур на душу населения, выделив не более трех групп с равными интервалами.
4. Известны следующие данные об успеваемости группы ФК-31 в зимнюю сессию по статистике (2004 года): 4, 3, 5, 4, 4, 3, 3, 2, 4, 5, 3, 2, 3, 2, 4, 3, 3, 4, 4, 5.
Постройте ряд распределения студентов по баллам оценок, полученных в сессию.
5. Имеются следующие данные о распределении населения Белгородской области по величине среднедушевых денежных доходов за 2003 г.:
| Доходы населения, руб. в месяц | В % |
| Все население в том числе со среднедушевыми денежными доходами до 1000,0 1000,1-1500,0 1500,1-2000,0 2000,1-3000,0 3000,1-4000,0 4000,1-5000,0 5000,1-7000,0 свыше 7000,0 | 100 5,6 11,6 13,9 24,8 16,8 10,3 10,1 6,9 |
// Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 113
Построить вторичную группировку данных о распределении населения по величине среднедушевых денежных доходов за 2003 г.: до 1500,0; 1500,1-2500,0; 2500,1-3500,0; 3500,1-4500,0; 4500,1-5500,0; 5500,1-6500,0; свыше 6500,0.
6. Известны следующие данные о результатах сдачи абитуриентами вступительных экзаменов в БГТУ им. В.Г. Шухова на факультет экономики и менеджмента в августе 2005 г. (баллов):
155 151 160 145 159 160 145
145 144 148 160 155 159 155
155 151 155 147 147 145 159
Постройте:
а) ряд распределения абитуриентов по результатам сдачи ими вступительных экзаменов, выделив четыре группы абитуриентов с равными интервалами;
б) ряд, делящий абитуриентов на поступивших и не поступивших в вуз, учитывая, что проходной балл составил 148 баллов.
Укажите, по какому группировочному признаку построен каждый из этих рядов распределения: атрибутивному или количественному?
7. Имеются следующие данные о распределении регионов городов по удельному весу убыточных предприятий на начало года (данные условные):
| Удельный вес убыточных предприятий | Число районов (городов) | Удельный вес, в % к итогу |
| до 10 | 7 | 10,1 |
| 10 - 20 | 12 | 48,6 |
| 20 и более | 20 | 41,3 |
| Итого: | 39 | 100,0 |
Произвести вторичную группировку районов по удельному весу убыточных предприятий, взяв за основу следующие группы: до 10, 10-15, 15-20, 20 и более.
8. Известно распределение населения по размеру среднедушевого дохода в Белгородской области за 2004 г.:
| № | Среднедушевой денежный доход в месяц, руб. | Численность населения, % |
| 1 | до 1000,0 | 3,2 |
| 2 | 1000,1 – 1500,0 | 8,0 |
| 3 | 1500,1 – 2000,0 | 10,9 |
| 4 | 2000,1 – 3000,0 | 22,5 |
| 5 | 3000,1 – 4000,0 | 17,7 |
| 6 | 4000,1 – 5000,0 | 12,3 |
| 7 | 5000,1 – 7000,0 | 13,6 |
| 8 | свыше 7000,0 | 11,8 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 67
В целях сопоставления данных распределить население Белгородской области в следующие группы:
| Среднедушевой денежный доход в месяц, руб. | Численность населения, млн. чел. |
| до 1500,0 | |
| 1500,1 – 2000,0 | |
| 2000,1 – 2500,0 | |
| 2500,1 – 3000,0 | |
| 3000,1 – 4000,0 | |
| 4000,1 – 5000,0 | |
| 5000,1 -6000,0 | |
| свыше 6000,0 |
9. Имеются следующие данные:
Основные показатели деятельности
аудиторско-консалтинговых групп России за 2004 г.
| № груп-пы | Совокуп-ная выручка, тыс. руб. | Прирост совокупной выручки за год, % | Среднее число специалис-тов, чел. | Число аттес-тованных аудиторов, чел. |
| 1 | 15441 | 6,2 | 35 | 12 |
| 2 | 14890 | 30,0 | 8 | 5 |
| 3 | 11439 | 11,5 | 10 | 5 |
| 4 | 13970 | 38,0 | 20 | 10 |
| 5 | 9959 | 28,1 | 18 | 9 |
| 6 | 7453 | 31,0 | 23 | 12 |
| 7 | 14790 | 1,9 | 12 | 7 |
| 8 | 8242 | 19,8 | 12 | 9 |
| 9 | 8811 | 36,8 | 11 | 7 |
| 10 | 12633 | 5,2 | 27 | 15 |
| 11 | 16189 | 51,8 | 12 | 10 |
| 12 | 14873 | 67,8 | 18 | 10 |
| 13 | 7958 | 47,8 | 11 | 5 |
| 14 | 9625 | 15,3 | 9 | 7 |
| 15 | 17312 | 21,9 | 20 | 8 |
| 16 | 11461 | 4,0 | 27 | 11 |
| 17 | 8587 | 11,7 | 14 | 9 |
| 18 | 8453 | 35,5 | 10 | 6 |
| 19 | 12701 | 48,5 | 26 | 13 |
| 20 | 17562 | 7,7 | 15 | 10 |
| 21 | 9521 | 3,8 | 24 | 14 |
| 22 | 13909 | 56,3 | 22 | 7 |
| 23 | 15870 | 28,9 | 36 | 18 |
| 24 | 8659 | 16,6 | 34 | 9 |
| 25 | 17801 | 23,5 | 40 | 18 |
| 26 | 11432 | 23,4 | 35 | 20 |
| 27 | 9398 | 11,5 | 40 | 8 |
| 28 | 14850 | 42,4 | 12 | 9 |
| 29 | 8290 | 17,6 | 17 | 6 |
| 30 | 10806 | 82,5 | 14 | 8 |
// www.raexpert.ru
На основе этих данных проведите анализ, взяв в качестве группировочного признака – совокупную выручку, выделив при этом не более 4-х групп с равными интервалами. Рассчитайте по каждой группе:
1) совокупную выручку;
2) среднее число специалистов;
3) число аттестованных аудиторов;
4) выручку на одного специалиста.
Результаты группировки представьте в табличной форме и сформулируйте выводы.
10. Следующие данные характеризуют распределение работников банка по величине заработной платы (данные условные):
| Заработная плата, долл. США | Численность работников, тыс. чел. |
| 90 – 160 160 – 230 230 – 300 300 – 370 370 – 440 440 – 510 510 – 580 580 – 650 650 – 720 720 – 790 790 – 860 860 и выше | 25 10 30 41 44 60 82 40 20 24 9 5 |
| Итого | 390 |
Используя приведенные данные, сделайте вторичную группировку, построив ряд распределения со следующими интервалами: до 150; 150 – 250; 250 – 350; 350 – 450; 450 – 550; 550 – 650; 650 – 750; 750 – 850; 850 и выше.
11. По приведенным ниже данным составьте статистическую таблицу, озаглавьте ее, определите подлежащее и сказуемое, а также вид представленной в таблице группировки по аналитической функции.
За 2003 год в Белгородской области введено в действие основных фондов на сумму 10371,0 млн. руб., в том числе в отрасли, производящие товары – 5883,0; в отрасли, оказывающие рыночные и нерыночные услуги – 4488,0 млн. руб.  Объем капиталовложений за этот же период в целом по Белгородской области составлял 14940,0 млн. руб., из них в отрасли, производящие товары 6513,1, в отрасли, оказывающие рыночные и нерыночные услуги – 8427,02 млн. руб.
Объем капиталовложений за этот же период в целом по Белгородской области составлял 14940,0 млн. руб., из них в отрасли, производящие товары 6513,1, в отрасли, оказывающие рыночные и нерыночные услуги – 8427,02 млн. руб. 
_______
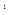 // Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 214
// Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 214
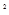 // Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 393
// Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 393
12. Результаты обследования работников малого предприятия по полу и уровню образования характеризуются следующими данными:
| № п/п | Пол | Образование |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | мужской мужской женский мужской женский мужской мужской мужской мужской женский мужской женский мужской мужской женский женский женский женский мужской женский женский мужской мужской женский мужской женский женский мужской женский мужской | среднее специальное незаконченное высшее среднее специальное среднее специальное среднее высшее среднее специальное среднее высшее высшее незаконченное высшее высшее среднее специальное высшее среднее специальное среднее специальное незаконченное высшее среднее среднее среднее специальное незаконченное высшее среднее высшее незаконченное высшее высшее среднее специальное высшее высшее незаконченное высшее среднее |
Произведите группировку работников: 1) по полу; 2) по уровню образования.
13. По приведенным ниже данным произведите группировку 30 негосударственных пенсионных фондов (НПФ) по величине общего объема пенсионных резервов, выделив четыре группы НПФ с открытыми интервалами.
Рассчитайте по каждой группе число НПФ, размер имущества для обеспечения уставной деятельности, количество специалистов НПФ, количество участников НПФ и количество участников НПФ, получающих негосударственную пенсию. Наряду с абсолютными размерами показателей, приведите относительные величины структуры.
Результаты группировки изложите в сводных групповых таблицах и проанализируйте.
Показатели деятельности негосударственных
пенсионных фондов (НПФ) России за 2004 г.
| № п/ п | Общий объем пенсион-ных резервов, тыс. руб. | Размер имущества для обеспечения уставной деятельности, тыс. руб. | Коли-чество специа-листов НПФ, чел. | Коли-чество участ-ников НПФ, чел. | Количество участников НПФ, получающих негосударствен-ную пенсию, чел. |
| 1 2 3 4 5 | 317079 312235 266373 168442 343286 | 23429 28173 75696 52364 72897 | 11 13 18 23 14 | 16674 8907 39524 11781 18169 | 152 8686 8408 1399 290 |
| 6 7 8 9 10 | 323523 133220 106011 229437 191748 | 18329 30629 49281 95333 16594 | 25 5 2 37 14 | 43228 3410 5134 82932 22438 | 16386 22 9 1570 762 |
| 11 12 13 14 15 | 119110 173838 198922 87930 231152 | 153161 31063 182505 35422 30000 | 10 11 11 7 31 | 5002 23977 6701 3565 40996 | 2 3723 334 239 695 |
| 16 17 18 19 20 | 153111 88691 102895 206541 192650 | 32689 4044 25770 30005 57000 | 11 8 9 29 14 | 31185 3019 40991 14316 15200 | 7941 127 1227 889 6354 |
| 21 22 23 24 25 | 100334 69904 6497 65075 53598 | 103330 11808 20651 8277 9200 | 4 50 4 8 14 | 7921 21134 341 14827 5479 | 5032 1727 23 707 84 |
| 26 27 28 29 30 | 50074 49767 44813 47743 63184 | 3881 16352 20648 25573 36102 | 5 4 4 11 12 | 253 2362 30113 19560 19864 | 28 295 39 267 276 |
// www.raexpert.ru
Тест
1. Распределение однородной совокупности по значениям варьирующего признака осуществляется с помощью группировки:
а) типологической;
б) структурной;
в) аналитической.
2. В ряду распределения семей по количеству детей вариантом является:
а) количество семей;
б) количество детей.
3. В ряду распределения городов по количеству жителей частотой является:
а) количество городов;
б) количество жителей.
4. В ряду распределения фирм по количеству занятых вариантом является:
а) количество занятых;
б) количество фирм.
5. В ряду распределения рабочих по разряду частотой является:
а) разряд рабочего;
б) количество рабочих.
6. Выявить взаимосвязь между признаками можно с помощью группировки:
а) типологической;
б) аналитической;
в) комбинационной;
г) структурной.
7. Наибольшее значение признака в интервале называется:
а) нижней границей;
б) верхней границей.
8. В классическом варианте аналитической группировки совокупность делится на группы по результативному признаку.
а) верно;
б) неверно.
9. Типологическая группировка применяется с целью:
а) выделения социально-экономических типов явлений;
б) изучения структуры явлений и структурных сдвигов, происходящих в них;
в) выявления связи и зависимости между явлениями;
г) изучения динамики социально-экономических явлений.
10. Равные интервалы при проведении группировки используются при условии, что значение признака в диапазоне вариации изменяются равномерно.
а) верно;
б) неверно.
11. Основанием группировки может быть:
а) качественный признак;
б) количественный признак;
в) как качественный, так и количественный признак.
12. Наименьшее значение признака в интервале называется:
а) нижней границей;
б) верхней границей.
13. Пользуясь формулой Стерджесса, определите интервал группировки сотрудников фирмы по уровню доходов, если общая численность сотрудников составляет 20 человек, а минимальный и максимальный доход соответственно равен 1500 и 5000 руб.:
а) 700 руб.;
б) 500 руб.;
в) 175 руб.
14. Определите по формуле Стерджесса число групп в группировке, если число единиц в совокупности равно 150:
а) 6;
б) 7;
в) 8;
г) 9.
15. Вторичной группировкой называют:
а) агрегирование первичных статистических данных;
б) распределение качественно неоднородной совокупности на классы;
в) формирование групп по дискретному вариационному признаку;
г) результаты перегруппировки данных.
16. Накопленные частоты используются при построении:
а) огивы;
б) гистограммы.
17. Полигон распределения используется для графического изображения:
а) дискретных вариационных рядов;
б) интервальных вариационных рядов;
в) кумулятивных рядов.
18. Вариационным рядом распределения является:
а) распределение промышленных предприятий по отраслям экономики;
б) распределение городов по количеству жителей;
в) распределение предприятий по организационно-правовой форме.
19. Какой вид статистического графика может использоваться для изображения ряда распределения?
а) диаграммы сравнения;
б) гистограмма;
в) диаграммы структуры;
20. Приведена группировка данных об уровне выполнения норм выработки рабочими двух цехов. Построить вторичную группировку, пересчитав данные цеха №1 в соответствии с группировкой цеха №2:
| Цех №1 | Цех №2 | ||
| Группы рабочих по % выполнения норм выработки | Число рабочих ( % к итогу) | Группы рабочих по % выполнения норм выработки | Число рабочих ( % к итогу) |
| до 90 | 2,0 | до 100 | 9,0 |
| 90 – 100 | 8,0 | 100 – 120 | 40,0 |
| 100 – 110 | 40,0 | 120 – 150 | 25,0 |
| 110 – 120 | 25,0 | 150 – 180 | 15,0 |
| 120 – 150 | 20,0 | 180 – 200 | 7,0 |
| 150 и выше | 5,0 | 200 и выше | 4,0 |
| Итого: | 100,0 | Итого: | 100,0 |
а) 8 б) 6 в) 10
1 13 65
20 120 20
20 30 2
25 27 1
26; 4; 2.
1.4 Графический способ изображения статистических показателей
1.4.1 Понятие о статистическом графике и его
основные элементы
Без применения графических изображений невозможно представить современную науку. Они стали незаменимыми в исследовательской работе и в международных сравнениях и сопоставлениях социально-экономических явлений.
Графическое изображение, прежде всего, позволяет осуществить контроль достоверности статистических показателей, так как представленные на графике они делают более очевидными имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления.
Графики также широко используются для изучения структуры явлений, их изменения во времени и размещения в пространстве. В них более выразительно проявляются сравниваемые характеристики и отчетливо видны основные тенденции развития и взаимосвязи, присущие изучаемому явлению или процессу.
Таким образом, статистический график - это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков.
Каждый график включает ряд основных элементов:
§ графический образ;
§ поле графика;
§ пространственные ориентиры;
§ масштабные ориентиры;
§ экспликацию графика.
Графический образ (основа графика) — это геометрические знаки, то есть совокупность точек, линий, фигур, с помощью которых изображаются статистические показатели. Важно правильно выбрать графический образ, который должен соответствовать цели графика и способствовать наибольшей выразительности изображаемых статистических данных.
Поле графика — это часть плоскости, где расположены графические образы. Поле графика имеет определенные размеры, которые зависят от назначения графика.
Пространственные ориентиры графика задаются в виде системы координатных сеток. Система координат необходима для размещения геометрических знаков в поле графика. Наиболее распространенной является система прямоугольных координат. Для построения статистических графиков используется обычно только первый и изредка первый и четвертый квадранты.
В практике графического изображения применяются также полярные координаты. Они необходимы для наглядного изображения циклического движения во времени.
Масштабные ориентиры статистического графика определяются масштабом и системой масштабных шкал. Масштаб статистического графика - это мера перевода числовой величины в графическую.
Масштабной шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа. Шкала имеет большое значение в графике. В ней различают три элемента:
1) линию (или носитель шкалы);
2) определенное число помеченных черточками точек, которые расположены на носителе шкалы в определенном порядке;
3) цифровое обозначение чисел, соответствующих отдельным помеченным точкам.
Как правило, цифровым обозначением снабжаются не все помеченные точки, а лишь некоторые из них, расположенные в определенном порядке. По правилам числовое значение необходимо помещать строго против соответствующих точек, а не между ними.
Носитель шкалы может представлять собой как прямую, так и кривую линию. В соответствии с этим различают шкалы прямолинейные (например, миллиметровая линейка) и криволинейные - дуговые и круговые (циферблат часов).
Экспликация - словесное описание содержания графика. Оно включает в себя название графика, которое должно в краткой форме передавать его содержание, подписи вдоль масштабных шкал и пояснения к отдельным частям графика.
1.4.2 Виды графических изображений и способы
их построения
Статистические графики по форме графического образа делятся на:
§ линейные (статистические кривые);
§ плоскостные:
- столбиковые;
- полосовые;
- квадратные;
- круговые;
- секторные;
- фигурные;
- точечные;
- фоновые;
§ объемные (поверхностные распределения).
По способу построения статистические графики делятся на:
§ диаграммы:
- диаграммы сравнения;
- структурные диаграммы;
- диаграммы динамики;
§ статистические карты:
- картограммы;
- картодиаграммы.
Диаграммы - наиболее распространенный способ графических изображений. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т.д. При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку.
Статистические карты - графики количественного распределения по поверхности. Они представляют собой условные изображения статистических данных на контурной географической карте, то есть показывают пространственное размещение и пространственную распространенность статистических данных.
При построении точечных диаграмм в качестве графических изображений применяются совокупности точек, при построении линейных применяются линии.
Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются в виде геометрических фигур и, в свою очередь, подразделяются на столбиковые, полосовые, круговые, квадратные, фигурные.
Статистические карты по графическому образу подразделяются на:
- картограммы;
- картодиаграммы.
В зависимости от круга решаемых задач выделяют:
§ диаграммы сравнения;
§ структурные диаграммы;
§ диаграммы динамики.
Особым видом графиков являются диаграммы распределения величин, представленных вариационным рядом:
§ гистограмма,
§ полигон,
§ огива,
§ кумулята.
1.4.3 Диаграммы сравнения
Диаграммы сравнения применяются для графического отображения статистических данных с целью их наглядного сопоставления друг с другом в тех или иных разрезах.
Сравнительные диаграммы делятся на:
§ диаграммы простого сопоставления;
§ структурные диаграммы;
§ изобразительные (фигур-знаков).
Диаграммы простого сопоставления дают наглядную сравнительную характеристику статистических совокупностей по какому-либо варьирующему признаку. При этом сопоставляемые совокупности и их части классифицируются по какому-либо атрибутивному или количественному признаку так, что отражаемый диаграммой статистический ряд представляет собой дискретный ряд цифр, на основе которого и строится график.
Диаграммы простого сопоставления между собой делятся на:
§ полосовые;
§ столбиковые.
Основной особенностью этих диаграмм является одномерность графического выражения величин варьирующего признака и их одномасштабность для различных столбцов или полос, характеризующих величину отражаемого признака в разных классификационных группах.
На столбиковых диаграммах статистические данные изображаются в виде вытянутых по вертикали прямоугольников. Построение столбиковой диаграммы требует применения вертикальной масштабной шкалы. Основания столбиков размещаются на горизонтальной линии, а высота столбиков устанавливается пропорционально изображаемым величинам.
При построении столбиковых диаграмм необходимо выполнять следующие требования: шкала, по которой устанавливается высота столбика, которая должна начинаться с нуля; шкала должна быть непрерывной; основания столбиков должны быть равны между собой; наряду с разметкой шкалы соответствующими надписями следует снабжать сами столбцы.
Пример: покажем построение столбиковой диаграммы по данным табл. 1.4.1, характеризующим количество частных предприятий и организаций в Белгородской области на 1 января за 1999 – 2005 гг. (рис. 1.4.1).
Таблица 1.4.1
Число частных предприятий и организаций
на 1 января за 1999– 2005 гг.
| Годы | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Число частных предприятий и организаций, тыс. | 12,0 | 12,8 | 14,6 | 15,8 | 17,5 | 18,8 | 17,0 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 106
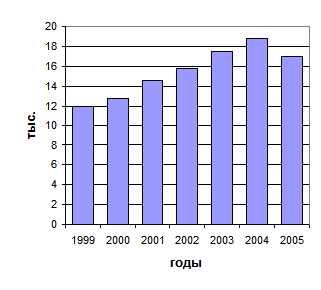
Рис. 1.4.1 Число частных предприятий и организаций в Белгородской области на 1 января за 1999 – 2005 гг.
Полосовые диаграммы (см. рис. 1.4.2) состоят из прямоугольников, расположенных горизонтально. В этом случае масштабная шкала - горизонтальная ось. Принцип их построения тот же, что и столбиковых.
Пример: покажем построение полосовой диаграммы по данным табл. 1.4.2, характеризующим денежные доходы населения Белгородской области за 1980 – 2004 гг. (рис. 1.4.2).
Таблица 1.4.2
Денежные доходы населения
за 1980 – 2004 гг.
| Годы | 1980 | 1990 | 1995 | 2000 | 2001 | 2002 | 2003 | 2004 |
| Денеж- ные доходы, млн. руб. | 1590,9 | 3263,5 | 6882,0 | 28061,9 | 38378,8 | 50053,7 | 60937,3 | 72916,2 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 65
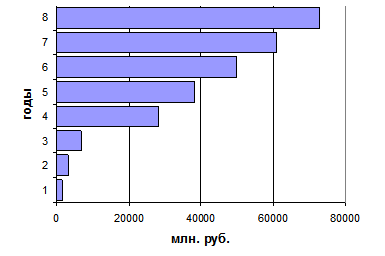
Рис. 1.4.2 Денежные доходы населения Белгородской области
за 1980 – 2004 гг.
Полосовые и столбиковые диаграммы являются однородными. Нетрудно заметить, что столбиковая диаграмма переходит в полосовую при повороте первой на 90 градусов. Выбор столбиковой или полосовой диаграммы в каждом конкретном случае равновозможен и обусловлен лишь эстетическими соображениями.
Размещение столбиков или полос в поле графика может быть различным:
§ на одинаковом расстоянии друг от друга;
§ вплотную друг к другу;
§ в частичном наложении друг на друга.
Более сложный вид принимают столбиковые и полосовые диаграммы при изображении на них статистических данных, показывающих какое-либо явление в нескольких разрезах. Такие диаграммы называются полосовыми или столбиковыми диаграммами с комбинированной группировкой показателей (см. рис. 1.4.3).
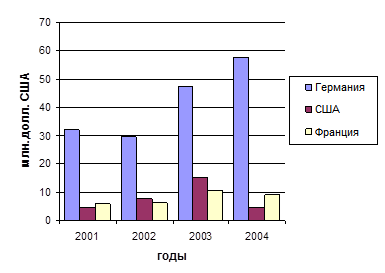
Рис. 1.4.3 Внешняя торговля (импорт) Белгородской области со странами вне СНГ за 2001 – 2004 гг. 
Для сопоставления изменяющихся во времени показателей, а также при сравнении величин, относящихся к одному и тому же периоду, могут использоваться квадратные и круговые диаграммы. В отличие от столбиковых или полосовых диаграмм они выражают величину изображаемого явления размером своей площади. Чтобы изобразить квадратную диаграмму, необходимо из сравниваемых статистических величин извлечь квадратные корни, а затем построить квадраты со сторонами, пропорциональными полученным результатам. Круговые диаграммы строятся аналогично. Разница состоит лишь в том, что на графике вычерчиваются круги, радиусы которых пропорциональны квадратному корню из изображаемых величин.
_________
 // Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 227
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 227
Например, если изобразить в виде кругов наличие собственных легковых автомобилей на 1000 человек населения Белгородской области за 2000 – 2002 гг., то сначала нужно извлечь квадратные корни из этих цифр (табл. 1.4.3).
Таблица 1.4.3
Наличие собственных легковых автомобилей на 1000 человек
населения Белгородской области за 2000 – 2002 гг.
| Годы | 2000 | 2001 | 2002 |
| Число собственных легковых автомобилей на 1000 человек населения, шт. | 137,3 | 148,0 | 158,6 |
// Белгородской области – 50 лет. Юбил. стат. сб./ Белгородский облкомстат. – 2003 г., с. 104
Это составит: за 2000 г. – 11,7; за 2001 г. – 12,2; за 2002 г. – 12,6. Затем установим масштаб и по этим данным построим круговую диаграмму (рис. 1.4.4).
Рис. 1.4.4 Рост числа собственных легковых автомобилей на 1000 человек населения Белгородской области за 2000 – 2002 гг.
Показательные диаграммы прямого сопоставления статистических величин могут быть сделаны более выразительными, легче схватываемыми и запоминаемыми, если простые геометрические фигуры заменить символами, воспроизводящими в какой-то степени внешний образ отображаемых графиком статистических совокупностей или символизирующими их.
Простейшей изобразительной диаграммой является такая в которой в качестве графических знаков служат силуэтные изображения - символы сравниваемых статистических совокупностей, пропорциональные по своим размерам объемам этих совокупностей. Следующим типом изобразительных диаграмм являются диаграммы, в которых используются знаки-символы как масштабные знаки, как орудия счета.
Как правило, фигурные диаграммы широко используются для рекламы.
1.4.4 Структурные диаграммы
Вторую большую группу показательных графиков составляют структурные диаграммы. Это такие диаграммы, в которых отдельные статистические совокупности сопоставляются по их структуре, характеризующейся соотношением разных параметров совокупности или ее отдельных частей.
Простейшим видом структурных статистических диаграмм являются диаграммы удельных весов, отражающие структуры сравниваемых совокупностей по процентному соотношению в них отдельных частей, выделяемых по тому или иному количественному или атрибутивному признаку. Эти диаграммы получаются путем преобразования простой полосовой диаграммы с подразделенными полосами. Полосовые диаграммы удельных весов могут вскрыть экономические существенные особенности многих изучаемых экономических явлений.
Другим методом графического изображения структур статистических совокупностей по соотношению удельных весов является составление структурных круговых или секторных диаграмм (рис. 1.4.5). Этот способ является наиболее распространенным, поскольку идея целого очень хорошо и наглядно выражается кругом, который представляет всю совокупность. Секторные диаграммы удобно строить следующим образом: вся величина явления принимается за сто процентов, рассчитываются доли отдельных частей в процентах. Круг разбивается на секторы пропорционально частям изображаемого целого.
Сумма всех углов круга, равная 360 градусов, приравнивается к 100%, а, следовательно, 1% принимается равным 3,6 градусов.
Пример: построим секторную диаграмму по данным таблицы 1.4.4.
Построение секторной диаграммы начинается с определения центральных углов секторов. Для этого процентное выражение отдельных частей совокупностей умножают на 3,6 градуса. Например, для данных таблицы 1.4.4.
2004 г.: 47,3*3,6  = 170,3
= 170,3  ; 52,7*3,6
; 52,7*3,6  = 189,7
= 189,7  ; 13,1*3,6
; 13,1*3,6  = 47,2
= 47,2  ; 9,0*3,6
; 9,0*3,6  = 32,4
= 32,4  ;12,6*3,6
;12,6*3,6  = 45,4
= 45,4  ; 3,1*3,6
; 3,1*3,6  =11,2; 14,9*3,6
=11,2; 14,9*3,6  = 53,6
= 53,6  .
.
По найденным значениям углов круги делятся на соответствующие секторы (рис. 1.4.5).
Таблица 1.4.4
Структура инвестиций в основной капитал по источникам финансирования в Белгородской области
(в процентах к итогу)
| 2004 | |
| Инвестиции в основной капитал – всего в том числе по источникам финансирования: собственные средства привлеченные средства из них: кредиты банков заемные средства других организаций бюджетные средства средства внебюджетных фондов прочие | 100 47,3 52,7 13,1 9,0 12,6 3,1 14,9 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 210
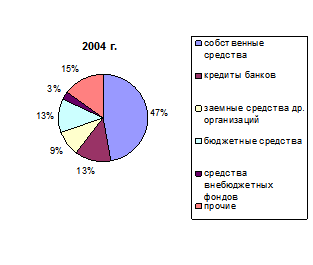
Рис. 1.4.5 Структура инвестиций в основной капитал по источникам финансирования в Белгородской области в 2004 г.
Секторные диаграммы выглядят убедительно при существенных различиях сравниваемых структур, а при небольших различиях она может быть недостаточно выразительна. Значительным преимуществом полосовых структурных диаграмм по сравнению с секторными диаграммами является их большая емкость, возможность отразить на небольшом пространстве большой объем полезной информации.
Для одновременного изображения трех величин, связанных между собой таким образом, что одна величина является произведением двух других, применяются диаграммы, называющиеся "знаком Варзара".
Знак Варзара представляет собой прямоугольник, у которого один сомножитель принят за основание, другой за высоту, а вся площадь равна произведению.
Например, произведение посевной площади и урожайности дает валовой сбор. Если в прямоугольнике одну сторону брать пропорционально посевной площади, а другую – урожайности, то площадь прямоугольника и представляет собой знак Варзара, то есть валовой сбор.
1.4.5 Диаграммы динамики
Линейные диаграммы целесообразно применять, если имеется ряд динамики с большим числом уровней. Линейные диаграммы воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать:
§ когда целью исследования является изображение общей тенденции и характера развития явления;
§ когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения;
§ когда наиболее существенным является сопоставление темпов роста, а не уровней.
Для построения линейных диаграмм используют систему прямоугольных координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т.д.), а по оси ординат - размеры отображаемых явлений или процессов. На оси ординат наносят масштабы. Особое внимание следует обратить на их выбор, так как от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в диаграмме, так как нарушение равновесия дает неправильное изображение развития явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Если в ряду динамики данные за некоторые годы отсутствуют, это должно быть уточнено при построении графика. Равным периодам времени и размерам уровня должны соответствовать равные отрезки масштабной шкалы.
Рассмотрим построение линейной диаграммы на основании данных таблицы 1.4.5.
Таблица 1.4.5
Динамика расходов консолидированного бюджета Белгородской области на социально – культурные мероприятия
за 2000-2004 гг.
| Годы | 2000 | 2001 | 2002 | 2003 | 2004 |
| Расходы, млн. руб. | 3139,5 | 3858,5 | 5617,9 | 6500,4 | 8329,7 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 193
В прямоугольной системе координат нанесем на ось абсцисс показатели времени, а на ось ординат – данные о динамике расходов консолидированного бюджета Белгородской области на социально – культурные мероприятия (рис. 1.4.6). Масштаб 0,5 см = 1000 млн. руб. Из графика видно, что положение кривой определяется не только данными о расходах бюджета, но и интервалами времени между датами.
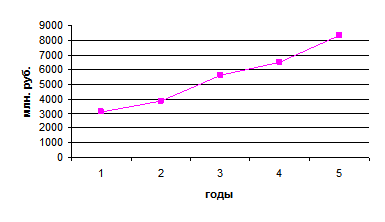
Рис. 1.4.6 Динамика расходов консолидированного бюджета Белгородской области на социально – культурные
мероприятия за 2000 – 2004 гг.
Нередко на одном линейном графике приводится несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя в разных странах. Примером графического изображения сразу нескольких показателей может служить рис. 1.4.7.
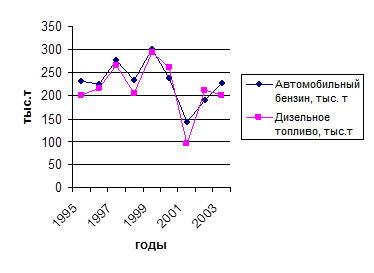
Рис. 1.4.7 Динамика ввоза горюче-смазочных материалов промышленными организациями оптовой торговли
в Белгородскую область за 1995 – 2003 гг. 
Линейные диаграммы с равномерной шкалой имеют один недостаток, снижающий их познавательную ценность. Этот недостаток заключается в том, что равномерная шкала позволяет измерять и сравнивать только отраженные на диаграмме абсолютные приросты или уменьшения показателей на протяжении исследуемого периода. Однако при изучении динамики важно знать относительные изменения исследуемых показателей по сравнению с достигнутым уровнем или темпы их изменения. Именно относительные изменения экономических показателей в динамике искажаются при изображении их на координатной диаграмме с равномерной вертикальной шкалой. Кроме того, в обычных координатах теряет всякую наглядность и даже становится невозможным изображение рядов динамики с резко изменяющимися уровнями, которые обычно имеют место в динамических рядах за длительный период времени.
_________
 // Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 332
// Белгородская область в 2003 году. Статистический сборник/ Белгородстат. – 2004, с. 332
В этих случаях следует отказаться от равномерной шкалы и положить в основу графика полулогарифмическую систему.
Полулогарифмической сеткой называется сетка, в которой на одной оси нанесен линейный масштаб, а на другой логарифмический. В данном случае логарифмический масштаб наносится на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (годам, кварталам, месяцам, дням и прочее). Техника построения логарифмической шкалы следующая: необходимо найти логарифмы исходных чисел; начертить ординату и разделить на несколько равных частей. Затем нанести на ординату (или равную ей параллельную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов. Далее записать соответствующие логарифмы чисел и их антилогарифмы, например (0,000; 0,3010; 0,4771; 0,6021; ...; 1,000, что дает 1, 2, 3, 4 ..., 10). Полученные антилогарифмы окончательно дают вид искомой шкалы на ординате. Логарифмический масштаб лучше понять на примере.
Допустим, нам надо изобразить на графике динамику продажи организациями оптовой торговли отдельных видов продовольственных товаров в Белгородской области за 1996 – 2002 гг. С этой целью находим логарифмы для каждого уровня ряда по каждому виду товаров (см. таблицу 1.4.6, где Y 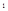 - мука, тыс. т; Y
- мука, тыс. т; Y 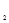 - сахар, тыс. т).
- сахар, тыс. т).
Таблица 1.4.6
Динамика продажи организациями оптовой торговли
отдельных видов продовольственных товаров
в Белгородской области за 1996 – 2004 гг.
| 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 
| 2003 | 2004 
| |
Y 
| 0,8 | 2,6 | 3,8 | 2,9 | 2,1 | 1,9 | 2,7 | 2,8 | 6,4 |
Y 
| 11,5 | 6,6 | 2,5 | 1,9 | 1,8 | 11,3 | 16,1 | 9,0 | 7,7 |
 // Белгородской области – 50 лет. Юбил. стат. сб./ Белгородский облкомстат. – 2003 г., с. 115
// Белгородской области – 50 лет. Юбил. стат. сб./ Белгородский облкомстат. – 2003 г., с. 115
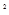 // Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 175
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 175
Найдя минимальное и максимальное значения логарифмов продажи организациями оптовой торговли отдельных видов продовольственных товаров, строим масштаб с таким расчетом, чтобы все данные разместились на графике. В соответствии с масштабом находим соответствующие точки, которые соединим прямыми линиями. В результате получим график (см. рис. 1.4.8) с использованием логарифмического масштаба на оси ординат. Полной логарифмической диаграммой он будет в том случае, если по оси абсцисс будет построен логарифмический масштаб. В рядах динамики это никогда не применяется, так как логарифмирование времени лишено всякого смысла.
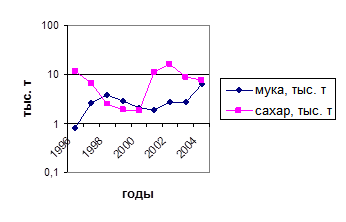
Рис. 1.4.8 Динамика продажи муки и сахара в Белгородской
области за 1996 – 2004 гг.
Разновидностью линейной диаграммы является радиальная диаграмма, построенная в полярных координатах и предназначенная для отражения процессов, ритмически повторяющихся во времени (см. рис. 1.4.9). Чаще всего эти диаграммы применяются для иллюстрации сезонных колебаний, и в этом отношении они имеют преимущество перед статистическими кривыми.
Радиальные диаграммы делятся на два вида:
§ замкнутые;
§ спиральные.
Эти два вида диаграмм отличаются друг от друга по технике построения, все завит оттого, что взято в качестве базы отсчета - центр круга или окружность. Замкнутые диаграммы отражают весь внутригодичный цикл динамики какого-либо одного года (рис. 1.4.9). Их построение сводится к следующему: вычерчивается круг, среднемесячный показатель приравнивается к радиусу этого круга, затем весь круг делится на двенадцать равных секторов, посредством проведения радиусов, которые изображаются в виде тонких линий. Каждый радиус изображает месяц, причем расположение месяцев аналогично циферблату часов. На каждом радиусе делается отметка в определенном месте, согласно масштабу, исходя из данных на соответствующий месяц. Если данные превышают среднегодовой уровень, то отметка делается вне окружности на продолжении радиуса. Затем отметки различных месяцев соединяются отрезками.
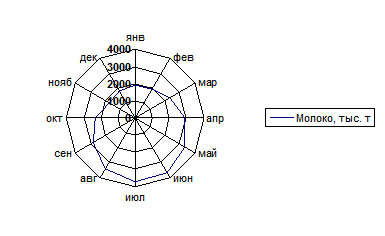
Рис. 1.4.9 Производство молока в хозяйствах всех категорий
в РФ за 2004 г. 
Если в качестве базы отсчета берется окружность, такого рода диаграммы называются спиральными (рис. 1.4.10).
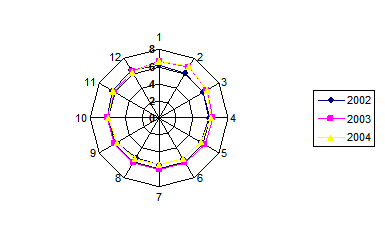
Рис. 1.4.10 Общая численность безработных в РФ по месяцам
за 2002-2004 гг. (на конец периода), млн. чел. 
_________
 // «Вопросы статистики» №6/ 2005, с. 73
// «Вопросы статистики» №6/ 2005, с. 73
 // «Вопросы статистики» №6/ 2005, с. 83
// «Вопросы статистики» №6/ 2005, с. 83
Спиральные диаграммы отличаются от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь динамический ряд в виде одной кривой. Особенно наглядна такая диаграмма тогда, когда наряду с сезонным ритмом ряд обнаруживает неуклонный рост из года в год.
1.4.6 Статистические карты
Карты статистические представляют собой вид графических изображений статистических данных на схематичной географической карте, характеризующих уровень или степень распространения того или иного явления на определенной территории.
Средствами изображения территориального размещения являются штриховка, фоновая раскраска или геометрические фигуры. Различают картограммы и картодиаграммы.
Картограмма - это схематическая географическая карта, на которой штриховкой различной густоты, точками или окраской различной степени насыщенности показывается сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления (например, плотность населения по областям или республикам, распределение районов по урожайности зерновых культур и т.п.). Картограммы делятся на фоновые и точечные.
Картограмма точечная - вид картограммы, где уровень какого-либо явления изображается с помощью точек. Точка изображает одну единицу совокупности или некоторое их количество, чтобы показать на географической карте плотность или частоту появления определенного признака.
Картограмма фоновая - вид картограммы, на которой штриховкой различной густоты или окраской различной степени насыщенности показывают интенсивность какого-либо показателя в пределах территориальной единицы.
Вторую большую группу статистических карт составляют картодиаграммы, представляющие собой сочетание диаграмм с географической картой. В качестве изобразительных знаков в картодиаграммах используются диаграммные фигуры (столбики, квадраты, круги, фигуры, полосы), которые размещаются на контуре географической карты. Картодиаграммы дают возможность географически отразить более сложные статистико-географические построения, чем картограммы.
Тренировочные задания
1. Изобразите при помощи столбиковой диаграммы данные о динамике потребительских цен на все товары и услуги населению Белгородской области в 2004 г.:
| Месяцы | ИПЦ на все товары и услуги, % |
| 1 | 101,8 |
| 2 | 101,1 |
| 3 | 99,9 |
| 4 | 101,5 |
| 5 | 100,3 |
| 6 | 100,6 |
| 7 | 100,8 |
| 8 | 100,6 |
| 9 | 101,0 |
| 10 | 101,6 |
| 11 | 101,0 |
| 12 | 101,1 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 216
Решение:
В соответствии с изложенными выше правилами на горизонтальной оси размещаются основания двенадцати столбиков на одинаковом расстоянии друг от друга, в данном случае 0,3 см. Ширина столбиков принята 0,5 см. Масштаб вертикальной оси – 0,5 % на 1 см. Наглядность диаграммы достигается сравнением величины столбиков (рис. 1.4.11).
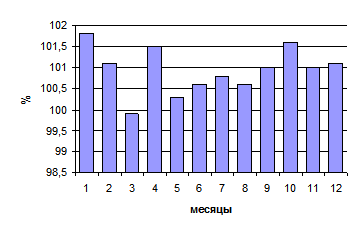
Рис. 1.4.11 Индексы потребительских цен на все товары и услуги населению Белгородской области в 2004 г.
2. Изобразите при помощи полосовой диаграммы данные о внешней торговли (экспорте) Белгородской области со странами вне СНГ за 2004 г. (млн. долл. США).
| Страны | Экспорт Белгородской области, млн. долл. США |
| Италия Румыния Чехия Польша Финляндия Турция | 44,7 40,0 13,3 23,1 1,7 7,3 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 227
Решение:
На вертикальной оси поместим основания шести полос на одинаковом расстоянии друг от друга, в данном случае 0,8 см. Ширина столбиков принята 0,7 см. Масштаб на горизонтальной оси – 10 млн. долл. США на 2 см. Наглядность диаграммы достигается сравнением величины полос (рис. 1.4.12).
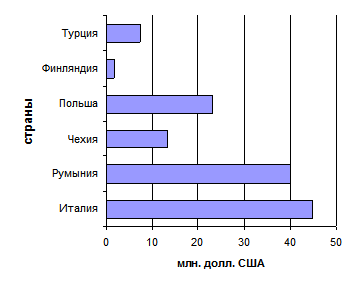
Рис. 1.4.12 Внешняя торговля (экспорт) Белгородской области
со странами вне СНГ за 2004 г.
3. При помощи столбиковой диаграммы изобразите данные о числе заключенных браков населением Белгородской области, тыс. чел.:
| 2000 | 2001 | 2002 | 2003 | 2004 |
| 9016 | 10764 | 10856 | 12318 | 9898 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 47
4. При помощи столбиковой диаграммы изобразите данные о числе совершенных разводов населением Белгородской области, тыс. чел.:
| 2000 | 2001 | 2002 | 2003 | 2004 |
| 6853 | 8214 | 8995 | 8194 | 6510 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 47
5. По данным о структуре доходов от оказания услуг подвижной электросвязи населению Белгородской области за 2000–2004 гг. постройте полигон распределения:
| Годы | 2000 | 2001 | 2002 | 2003 | 2004 |
Подвижная электросвязь  , % , %
| 2,0 | 0,9 | 1,3 | 0,6 | 43,1 |
 С 2004 г. учитываются организации ОАО «Вымпелком-регион» и ОАО «Реком»
С 2004 г. учитываются организации ОАО «Вымпелком-регион» и ОАО «Реком»
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 161
6 . По данным о структуре продаж алкогольных напитков и пива населению Белгородской области постройте диаграммы, изображающие структуру. Укажите, к какому виду графиков они относятся.
| Показатель | Годы | |
| 1990 | 2002 | |
| Алкогольные напитки и пиво, % Всего: | 100,0 | 100,0 |
| В том числе: Водка и ликероводочные изделия | 61,6 | 78,2 |
| Виноградные и плодовые вина | 23,6 | 9,4 |
| Коньяк | 4,3 | 0,8 |
| Шампанские и игристые вина | 0,9 | 2,0 |
| Пиво | 9,6 | 9,6 |
// Белгородской области – 50 лет. Юбил. стат. сб./ Белгородский облкомстат. – 2003 г., с. 112
7. При помощи квадратной диаграммы сопоставьте следующие данные о городском жилищном фонде в Белгородской области за 2000 -2004 гг. (млн. кв. м.):
| 2000 | 2001 | 2002 | 2003 | 2004 |
| 19,2 | 19,7 | 20,1 | 20,5 | 21,0 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 73
8 . С помощью фигур-знаков изобразите графически данные о продаже цемента по Белгородской области за 2002 - 2004 гг., тыс. т:
| 2002 | 2003 | 2004 |
| 25,6 | 34,0 | 40,8 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 175
9. Изобразите в виде квадратной и круговой диаграммы данные о реализации шин по Белгородской области за 2002 – 2004 гг., тыс. шт.:
| 2002 | 2003 | 2004 |
| 12,3 | 14,9 | 23,7 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 175
10. По данным о перевозках пассажиров по видам транспорта общего пользования в Белгородской области за 2002 - 2004 гг. (млн. чел.) постройте диаграммы:
а) квадратные; б) круговые; в) секторные.
| 2002 | 2003 | 2004 | |
| Транспорт - всего | 298,3 | 275,7 | 248,8 |
| в том числе: железнодорожный автобусный троллейбусный трамвайный воздушный, тыс. | 8,4 188,2 91,5 10,2 37,4 | 7,5 180,1 10,7 77,4 41,2 | 7,5 156,0 9,7 75,6 49,0 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 154
11. Постройте радиальную диаграмму по данным об объеме платных услуг населению РФ по месяцам за 2004 год, млрд. руб.:
| I | II | III | IV | V | VI | VII | VIII | IX | Х | XI | XII |
| 125,2 | 126,9 | 136,0 | 138,5 | 139,3 | 146,8 | 153,9 | 155,6 | 157,8 | 156,6 | 158,7 | 170,8 |
// «Вопросы статистики» №6/2005, с. 80
12. Имеются следующие данные:
| Российская Федерация | Центральный федеральный округ | Белгородская область | |
| Территория на 01.01.2003 г., тыс. кв. км. Численность населения, тыс. чел. | 17075,4 145181,9 | 650,7 37991,0 | 27,1 1512,4 |
// Белгородской области – 50 лет. Юбил. стат. сб./ Белгородский облкомстат. – 2003 г., с. 27
Построить картограмму “Плотность населения РФ, Центрального федерального округа и Белгородской области на 01.01.2003 г.”:
а) точечную;
б) фоновую.
Что показывает построенная картограмма?
13. Имеются следующие данные, характеризующие динамику внешней торговли Белгородской области (млн. долл. США):
| Годы | Внешнеторговый оборот | В том числе | |
| экспорт | импорт | ||
| 1996 1997 1998 1999 2000 2001 2002 2003 2004 | 1072 1023 1056 871 1062 1385 1103 1615 2290 | 713 601 581 376 473 581 498 696 976 | 359 422 475 495 589 804 605 919 1315 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 226
Постройте линейные диаграммы. Сделайте выводы.
14. По данным последней Всероссийской переписи населения о конфессиональной принадлежности жителей России постройте секторную диаграмму:
| Конфессиональная принадлежность жителей России | В % |
| Численность взрослого населения России всего: в том числе: Православные Мусульмане Буддисты Иудеи Прочие конфессии Атеисты Верующие вне конфессий | 100,0 62,0 6,7 0,3 0,2 1,8 15,0 14,0 |
// «Эксперт» №27 (474), 2005
15. Дана структура оборота розничной торговли по формам собственности в Белгородской области за 2000-2004 гг. (в процентах к итогу).
| 2000 | 2001 | 2002 | 2003 | 2004 | |
| Оборот розничной торговли – всего в том числе по формам собственности: государственная и муниципальная частная прочие | 100 3,2 89,6 7,2 | 100 2,9 90,9 6,2 | 100 2,6 91,4 6,0 | 100 2,1 92,5 5,4 | 100 1,7 92,4 5,9 |
// Белгородская область в цифрах в 2004 году. Крат. стат. сб./ Белгородстат. – 2005, с. 169
Постройте линейные диаграммы. Сделайте выводы.
16. Постройте диаграмму удельных весов по данным о структуре импорта фруктов в Россию, полученных от группы компаний JFC, %:
| Импорт | |
| Бананы Цитрусовые Яблоки Груши Виноград Остальные | 27 26 20 7 5 15 |
| Всего | 100 |
// «Эксперт» №5 (452), 2005
Тест
1. Графики количественного распределения по поверхности называются:
а) диаграммы;
б) статистические карты.
2. Для изображения взаимосвязи между факторными и результативными признаками на графике применяются диаграммы:
а) столбиковые;
б) линейные.
3. Какие виды статистических графиков могут использоваться для изображения рядов распределения:
а) диаграммы сравнения;
б) диаграммы структуры;
в) кумулята.
4. Простейшим видом структурных статистических диаграмм являются:
а) секторные диаграммы;
б) диаграммы удельных весов.
5. При построении линейных диаграмм используются масштабные шкалы:
а) равномерные;
б) логарифмические.
6. Вид графических изображений статистических данных на схематичной географической карте, характеризующих уровень или степень распространения того или иного явления на определенной территории – это:
а) полулогарифметическая сетка;
б) карта статистическая.
7. Какие диаграммы получаются путем преобразования простой полосовой диаграммы с подразделенными полосами?
а) диаграммы удельных весов;
б) секторные диаграммы.
8. Назовите вид радиальной диаграммы:
а) спиральная;
б) плоскостная.
9. Для одновременного изображения трех величин, связанных между собой таким образом, что одна величина является произведением двух других, применяются диаграммы, называющиеся -
а) “знаком Варзара”;
б) моделью Лоренца.
10. Изобразительными знаками в картодиаграммах являются:
а) точки и штриховка; б) круги, квадраты и другие фигуры.
1.5 Статистические показатели
1.5.1 Понятие, формы выражения и виды статистических показателей
Понятие системы показателей
Статистический показатель представляет собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности.








