В случае, когда размах вариации признака в совокупности велик и значения признака варьируют неравномерно, то надо использовать группировку с неравными интервалами.
Величина интервалов, изменяющихся в арифметической и геометрической прогрессии, определяется следующим образом:
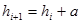 , (1.3.3)
, (1.3.3)
а в геометрической прогрессии:
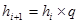 , (1.3.4)
, (1.3.4)
где а - константа: для прогрессивно-возрастающих интервалов имеет знак «+», и знак «-» - для прогрессивно-убывающих;
q - константа: больше «1» - для прогрессивно-возрастающих и меньше «1» - в другом случае.
Применение неравных интервалов обусловлено тем, что в первых группах небольшая разница в показателях имеет большое значение, а в последних группах эта разница не существенна.
Например, при построении группировки предприятий легкой промышленности по показателю объем произведенной продукции за год, который варьирует от 1,0 млн. руб. до 150,0 млн. руб., нецелесообразно рассматривать равные интервалы, т.к. учитываются как малые, так и крупнейшие предприятия отрасли. Поэтому следует образовывать неравные интервалы: 1,0-10,0; 10,0-50,0; 50,0-150,0.
Интервалы группировок могут быть:
§ закрытыми;
§ открытыми.
Закрытыми называются интервалы, у которых имеются верхняя и нижняя границы.
Открытые - это те интервалы, у которых указана только одна граница: верхняя - у первого, нижняя - у последнего. Например, группы коммерческих банков по числу работающих в них сотрудников (чел.): до 200, 200-300, 300-400, 400 и более.
При группировке единиц совокупности по количественному признаку границы интервалов могут быть обозначены по-разному, в зависимости от того, непрерывный это признак или дискретный.
Если основанием группировки служит непрерывный признак, например, группы строительных фирм по объему основных средств (млн. руб.): 120-390, 390-660, 660-930, 930-1200, то одно и то же значение признака выступает и верхней и нижней границами двух смежных интервалов. В данном случае объем работ 390 млн. руб. составляет верхнюю границу первого интервала и нижнюю границу второго, 660 млн. руб. - соответственно второго и третьего и т. д., т. е. верхняя граница i - го интервала равна нижней границе (i+1) - го интервала.
При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы объекта, значения признака у которых совпадают с границами интервалов. Например, во вторую или третью группу должна войти строительная фирма с объемом основных средств 660 млн. рублей?
Если верхняя граница формируется по принципу «исключительно», то фирма должна быть отнесена к третьей группе, в противном случае – ко второй. Для того чтобы правильно отнести к той или иной группе единицу объекта, значение признака которой совпадает с границами интервалов, можно использовать открытые интервалы (по нашему примеру группы строительных фирм по объему основных средств преобразуются в следующие: до 390, 390-660, 660-930, 930 и выше). В данном случае, вопрос отнесения отдельных единиц совокупности, значения которых являются граничными, к той или иной группе решается на основе анализа последнего открытого интервала.
Возможны два случая обозначения последнего открытого интервала:
1) 930 млн. руб. и более;
2) более 930 млн. руб.
В первом случае, строительные фирмы с объемом работ 930 млн. руб. попадут в третью группу; во втором случае - во вторую группу.
Если в основании группировки лежит дискретный признак, то нижняя граница i-го интервала равна верхней границе i-1-го интервала, увеличенной на 1. Например, группы строительных фирм по числу занятого персонала (чел.) будут иметь вид: 500-650, 651-700, 701-800.
При определении границ интервалов статистических группировок иногда исходят из того, что изменение количественного признака приводит к появлению нового качества. В этом случае граница интервала устанавливается там, где происходит переход от одного качества к другому. Строя такую группировку, следует дифференцированно устанавливать границы интервалов для разных отраслей народного хозяйства. Это достигается путем использования группировок со специализированными интервалами.
Специализированные - это такие интервалы, которые применяются для выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях.
При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно-возрастающими, ни прогрессивно-убывающими. Такие интервалы называются произвольными и, как правило, используются при группировке предприятий, например, по уровню рентабельности.
Пример: произведем анализ крупнейших российских страховых компаний по итогам 2004 г., применяя метод группировок, таблица 1.3.1.
Таблица 1.3.1
Основные показатели деятельности
российских страховых компаний по итогам 2004 г.
| № компании | Страховые взносы, млн. руб. | Собственные средства, млн. руб. | Уровень выплат, % |
| 1 | 23528 | 4859 | 36 |
| 2 | 16366 | 3444 | 44 |
| 3 | 12516 | 2879 | 68 |
| 4 | 11395 | 2066 | 58 |
| 5 | 10137 | 2096 | 40 |
| 6 | 7942 | 2103 | 48 |
| 7 | 6724 | 1384 | 60 |
| 8 | 6260 | 1979 | 26 |
| 9 | 6195 | 6044 | 29 |
| № компании | Страховые взносы, млн. руб. | Собственные средства, млн. руб. | Уровень выплат, % |
| 10 | 3432 | 7668 | 16 |
| 11 | 6949 | 996 | 18 |
| 12 | 3831 | 627 | 33 |
| 13 | 3321 | 1031 | 36 |
| 14 | 3134 | 767 | 39 |
| 15 | 3069 | 887 | 28 |
| 16 | 2526 | 1336 | 69 |
| 17 | 2403 | 660 | 39 |
| 18 | 1849 | 1581 | 45 |
| 19 | 14174 | 670 | 77 |
| 20 | 6930 | 637 | 94 |
| 21 | 5288 | 562 | 25 |
| 22 | 3862 | 756 | 12 |
| 23 | 2784 | 475 | 31 |
| 24 | 2215 | 1020 | 57 |
| 25 | 1458 | 430 | 52 |
| 26 | 1429 | 543 | 11 |
| 27 | 1354 | 392 | 48 |
| 28 | 1345 | 397 | 48 |
| 29 | 1188 | 1349 | 26 |
| 30 | 2807 | 693 | 14 |
// «Эксперт» №18 (465), 2005
В качестве группировочного признака возьмём страховые взносы. Образуем 4 группы страховых компаний с равными интервалами.
Величину интервала определим по формуле:
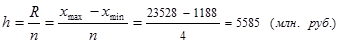
Обозначим границы групп: 1188 – 6773 - 1-я группа;
6773 – 12358 - 2-я группа;
12358 – 17943 - 3-я группа;








