Тема: Применение математических методов в профессиональной деятельности среднего медицинского персонала
Специальность: 31.02.01 Лечебное дело
Дисциплина: ЕН.02 Математика
111
Лекция №21
Количество часов: 2ч
Тема: Применение математических методов в профессиональной деятельности среднего медицинского персонала
При выполнении своих профессиональных обязанностей медицинским работникам часто приходится производить различные математические вычисления. От правильности проведенных расчетов зависит здоровье, а иногда и жизнь пациентов. В этом разделе рассмотрим наиболее часто встречающиеся ситуации, где необходимо применение математических методов.
В хозяйственных и статистических расчетах, во многих отраслях науки части величин принято выражать в процентах. Очень часто на практике приходится встречаться со случаями приготовления растворов с определенной массовой долей растворенного вещества, смешением двух растворов разной концентрации или разбавлением крепкого раствора водой.
В данной теме рассмотрены типовые задачи на проценты и методы их решения.
Обучающийся должен уметь:
решать основные задачи на проценты; решать задачи на смеси, сплавы, растворы;
составлять и решать пропорции; рассчитывать концентрацию раствора; рассчитывать количество сухого вещества на заданный объем жидкости.
Обучающийся должен знать:
определение процента; определение концентрации растворов; методы решения задач на проценты.
Пропо́рция
1.Пропо́рция (лат. proportio — соразмерность, выровненность частей), равенство двух отношений, т. е. равенство вида a : b = c : d, или, в других обозначениях, равенство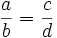 
(часто читается как: «a относится к b так же, как c относится к d»). Если a : b = c : d, то a и d называют крайними, а b и c — средними членами пропорции.
Основные свойства пропорций
Обращение пропорции. Если a : b = c : d, то b : a = d : c
Перемножение членов пропорции крест-накрест. Если a : b = c : d, то ad = bc.
Перестановка средних и крайних членов. Если a : b = c : d, то
a : c = b : d (перестановка средних членов пропорции),
d : b = c : a (перестановка крайних членов пропорции).
Увеличение и уменьшение пропорции. Если a : b = c : d, то
(a + b) : b = (c + d) : d (увеличение пропорции),
(a – b) : b = (c – d) : d (уменьшение пропорции).
Составление пропорции сложением и вычитанием. Если a : b = c : d, то
(a + с) : (b + d) = a : b = c : d (составление пропорции сложением),
(a – с) : (b – d) = a : b = c : d (составление пропорции вычитанием).
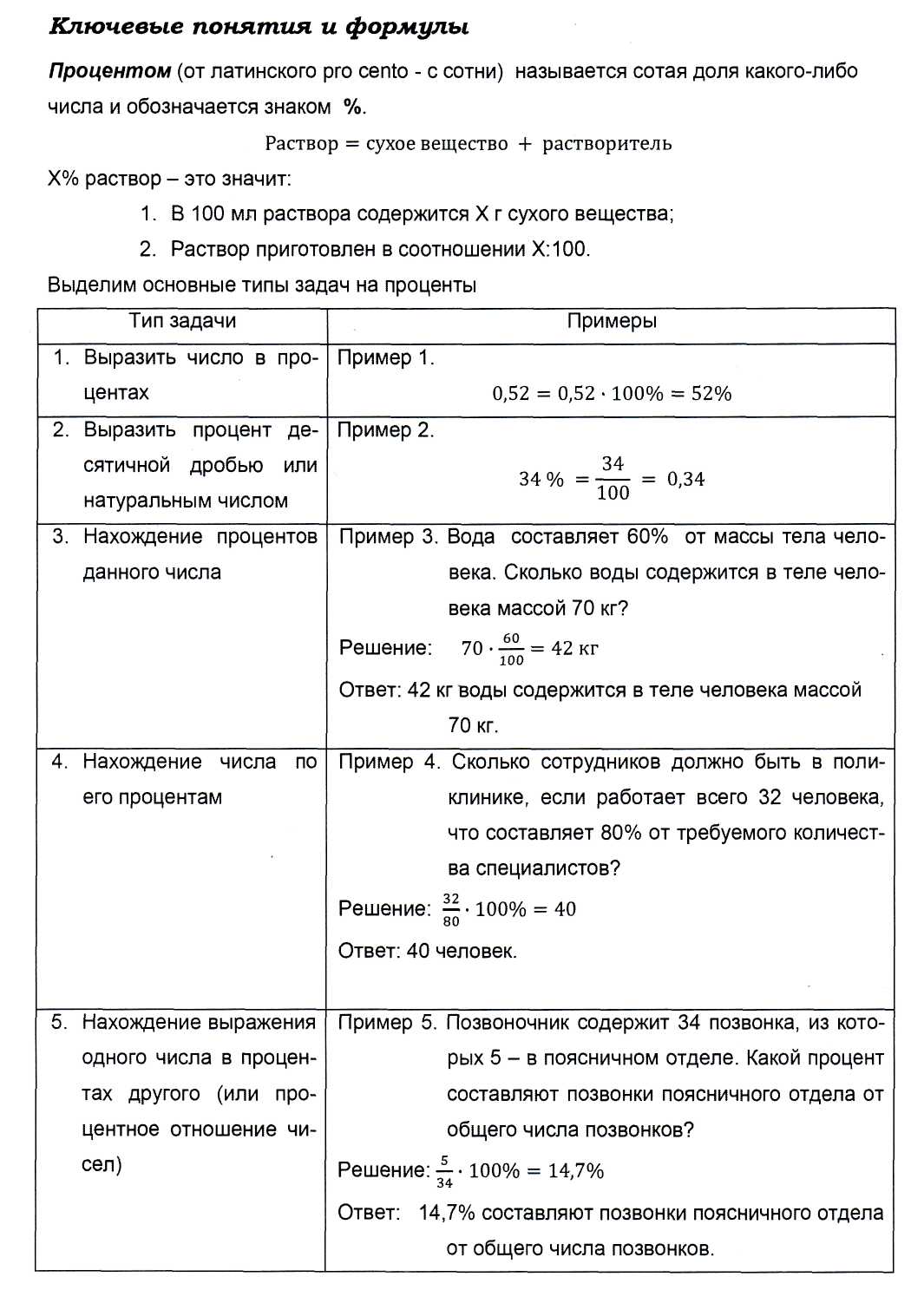
2.Проценты
Процент – одна сотая часть числа.
Нахождение p % числа A: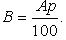 
Нахождение числа A, если p % его равны B: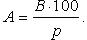 
Пропорциональность
Пропорция – равенство двух отношений: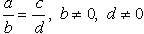 
(a, d – крайние члены пропорции; b, c – средние члены пропорции).
Основное свойство пропорции: ad=bc.
Выражение члена пропорции через остальные:
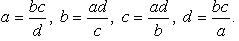
Применение математических методов
в профессиональной деятельности среднего медицинского персонала
Практические задания
1.
Определить процентную концентрацию раствора, приготовленного в соотношении:
а) 1:1000; б) 2:5000; в) 3:6000; г) 4: 1000; д) 9:2000.
2.
Определить концентрацию в соотношении, если процентная концентрация составила:
а) 0,4 %; б) 0,08%; в)0,005%; г) 0,25%; д) 0,1%.
3.
Отделение функциональной диагностики обслуживало 40 человек в день.
После внедрения компьютерных технологий пропускная способность отделения увеличилась на 35%. Сколько человек стало обслуживать отделение?
4.
С наступлением холодов количество больных с острыми респираторными
заболеваниями (ОРЗ) увеличилось до 15 человек в день, а до этого составляло около 10 человек. На сколько процентов возросло число больных с ОРЗ?
5.
26 человек поступили в травмпункт с переломом конечностей, что составило 13% от всех обратившихся. Сколько человек поступило в травмпункт?
6.
Объем крови в организме человека составляет 7% от массы тела. В малом круге кровообращения содержится 20-25%, а в большом - 75-85%. Определите объем циркулирующей крови в большом круге кровообращения человека весом 90 кг.