Совместные и несовместные события.
ПЛАН ЗАНЯТИЯ
Дисциплина: ЕН.03 Теория вероятностей и математическая статистика
Преподаватель: Старченко Е.А
Курс: 3
Группа: 1 ПКС-20
Специальность: 09.02.03 Программирование в компьютерных системах»
Дата: 21.09.22
Время проведения: 11.50-13.20, 3 пара
Тема: Случайные события. Достоверные, невозможные события
Цель занятия:
дидактическая: сформировать понятие случайного события, изучить виды событий.
развивающая: развивать абстрактное мышление, логику
Вид занятия лекция
Литература
Теория вероятностей и математическая статистика : учеб. пособие / Е. А. Трофимова, Н. В. Кисляк, Д. В. Гилёв ; [под общ. ред. Е. А. Трофимовой] ; М-во образования и науки Рос. Федерации, Урал. федер. ун-т. – Екатеринбург : Изд-во Урал. ун-та, 2018, стр. 8
Интернет-ресурсы:
https://poisk-ru.ru/s201t10.html
ЗАДАНИЕ: законспектировать лекцию, ответить на контрольные вопросы. Работы в электронном виде отправить для проверки.
КОНСПЕКТ ЛЕКЦИИ
План
1. Виды событий
2. Операции над событиями и их свойства
В естественных науках познание действительности происходит в результате испытаний (экспериментов) или наблюдений, т. е. опыта в широком понимании слова.
Под испытанием (наблюдением), в общем смысле, подразумевается наличие определенного комплекса условий. Возможный результат — исход испытания или наблюдения — называется событием, независимо от его значимости.
Элементарное событие (исход) – событие, которое нельзя разложить на более простые (обозначают w).
Сложное событие – событие, которое можно разложить на более простые.
Пример. Событие, состоящее в получении месячного дохода в сумме 5,1 тыс. руб. является элементарным, а в интервале от 5 до 6 тыс. руб. – сложным.
При построении теории события идеализируются, т. е. игнорируются ситуации, несущественные для данного явления.
1. Виды событий
События бывают достоверными, невозможными и случайными.
1) Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.
2) Невозможным называют событие, которое в результате испытания заведомо не произойдёт. Пример невозможного события: в условиях земного тяготения подброшенная монета трах-тибидох улетит вверх.
3) И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. Пример: в результате броска монеты выпадет «орёл». В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила и направление броска, сопротивление воздуха и т.д.
Подчёркнутый критерий случайности очень важен – так, карточный шулер может очень ловко имитировать случайность и давать выигрывать клиенту, но ни о каких случайных факторах, влияющих на итоговый результат, речи не идёт.
Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события. В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл, выпадет решка. Естественно, подразумевается, что данное испытание проводится в таких условиях, что монета не может встать на ребро или, скажем, зависнуть в невесомости.
События (любые) обозначают большими латинскими буквами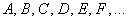 
либо теми же буквами с подстрочными индексами, например: 
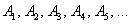. При этом стараются избегать буквы 
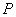, которая зарезервирована под другие нужды.
Запишем следующие случайные события:
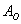– в результате броска монеты выпадет «орёл»;
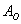
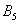– в результате броска игральной кости (кубика) выпадет 5 очков;
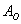
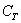– из карточной колоды будет извлечена карта трефовой масти.
Да, события прямо так и записывают в практических задачах, при этом в уместных случаях удобно использовать «говорящие» подстрочные индексы (хотя можно обойтись и без них).
И следует в третий раз подчеркнуть, что случайные события обязательно удовлетворяют вышеприведённому критерию случайности. В этом смысле особо показателен 3-й пример: если из колоды изначально удалить все карты трефовой масти, то событие 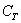становится невозможным. Наоборот, если испытателю известно, что, например, дама треф лежит снизу, то он при желании может сделать событие 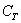достоверным =) Таким образом, в данном примере предполагается, что карты хорошо перемешаны и их «рубашки» неразличимы, т.е. колода не является краплёной.
Важной характеристикой случайных событий является их равновозможность. Два или большее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другое. Например:
– выпадение орла или решки при броске монеты;
– выпадение 1, 2, 3, 4, 5 или 6 очков при броске игрального кубика;
– появление трефы, пики, бубны или червы при случайном извлечении карты из полной колоды.
При этом предполагается, что монета и кубик однородны и имеют геометрически правильную форму, а колода хорошо перемешана и «идеальна» с точки зрения неразличимости рубашек карт.
Совместные и несовместные события.
Могут ли быть те же события НЕ равновозможными? Легко. Так, если у монеты или кубика смещён центр тяжести, то гораздо чаще будут выпадать вполне определённые грани. Если кто-то ловко спрятал в рукаве туза треф, то становится менее возможным, что оппоненту будет сдана трефа, и, главное, менее возможно, что будет сдан туз.
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
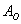– в результате броска монеты выпадет орёл;
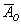– в результате этого же броска выпадет решка.
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
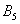– в результате броска игрального кубика выпадет 5 очков;
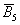– в результате этого же броска выпадет число очков, отличное от пяти.
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
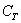– из колоды будет извлечена карта трефовой масти, либо
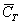– извлечена пика, черва или бубна.
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий.
Очевидно, что любая пара противоположных событий, например, 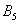и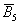 
(выпадение / невыпадение «пятёрки») образует полную группу. Но, разумеется, полную группу могут образовывать не только противоположные события:
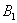– в результате броска игрального кубика выпадет 1 очко;
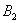– … 2 очка;
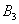– … 3 очка;
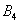– … 4 очка;
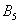– … 5 очков;
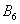– … 6 очков.
События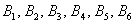 
несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания обязательно появится одно из этих шести событий).
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 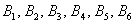элементарны, но событие 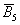не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).
В примере с картами события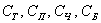 
(извлечение трефы, пики, червы или бубны соответственно) несовместны и образуют полную группу, но они неэлементарны. Если считать, что в колоде 36 карт, то каждое из перечисленных выше событий включает в себя 9 элементарных исходов. Аналогично – события 
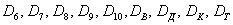(извлечение шестёрки, семёрки, …, короля, туза) несовместны, образуют полную группу и неэлементарны (каждое включает в себя 4 исхода).
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных.
События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого.
Например:
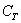– из колоды карт будет извлечена трефа;
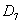– из колоды карт будет извлечена семёрка.
Данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.