Теорема умножения вероятностей.
Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило:
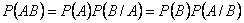
Доказательство. Докажем теорему для случая, когда опыт имеет конечное число несовместных равновероятных исходов.
Пусть:
· событие  появилось в
появилось в 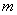 исходах опыта;
исходах опыта;
· событие 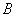 появилось в
появилось в 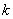 исходах опыта;
исходах опыта;
· событие 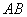 появилось в
появилось в 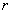 исходах опыта.
исходах опыта.
Вероятность события 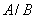 вычислим по классическому определению. Поскольку событие
вычислим по классическому определению. Поскольку событие 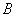 произошло, то всего возможных в этом случае исходов -
произошло, то всего возможных в этом случае исходов - 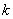 ; при этом из этих
; при этом из этих 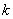 возможных исходов благоприятны событию
возможных исходов благоприятны событию  те исходы, которые составляют событие
те исходы, которые составляют событие 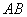 , т.е.
, т.е. 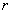 исходов:
исходов:
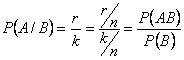 ,
,
или
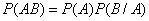 .
.
Следствие 1. Обобщим теорему на случай трех событий:
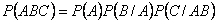
Следствие 2. Обобщим теорему на случай  событий: в случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились:
событий: в случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились:
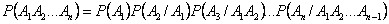 .
.
Пример. В группе 20 студентов. Из них двое курят, 12 – в очках, 6 – курят и носят очки. Найти вероятность того, что студент курит, если он носит очки.
Решение. Пусть событие  - студент курит;
- студент курит; 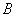 - студент носит очки.
- студент носит очки.

Тогда
 .
.
Заметим, что условная и безусловная вероятности события  в данной задаче различны:
в данной задаче различны: 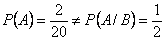 .
.
События называются независимыми, если появление одного из них не влияет на вероятность появления другого: 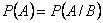 .
.
Если события независимые, то теорема умножения вероятностей принимает вид:
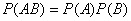 - критерий независимости событий.
- критерий независимости событий.
В рассмотренном примере события  и
и  - зависимы, поскольку
- зависимы, поскольку
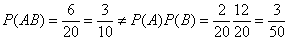 .
.
Пример. Бросают три монетки и игральную кость. Событие  - выпал герб, событие
- выпал герб, событие  - выпало число очков, равное 6. Пространством элементарных исходов опыта является множество
- выпало число очков, равное 6. Пространством элементарных исходов опыта является множество 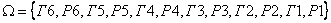 . Тогда
. Тогда 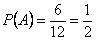 ,
, 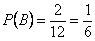 ,
, 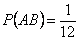 . Таким образом,
. Таким образом, 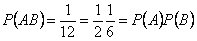 , т.е. события
, т.е. события  и
и 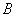 - независимы.
- независимы.
Свойства независимых событий
Теорема
Если события  и
и 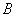 независимы, то:
независимы, то:
1) события  и
и 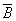 независимы;
независимы;
2) события 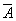 и
и 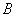 независимы;
независимы;
3) события 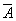 и
и 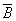 независимы.
независимы.
Доказательство. 1) 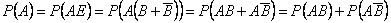
Поскольку события  и
и 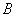 независимы, то:
независимы, то:
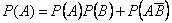 .
.
Итак,
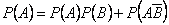
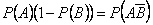 .
.
Поскольку 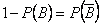 , то
, то 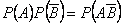 , что свидетельствует о независимости событий
, что свидетельствует о независимости событий  и
и 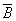 .
.
2) 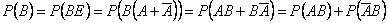
Поскольку события  и
и 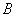 независимы, то:
независимы, то:
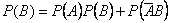 .
.
Итак,
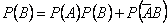
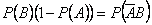 .
.
Поскольку 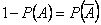 , то
, то 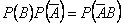 , что свидетельствует о независимости событий
, что свидетельствует о независимости событий 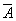 и
и 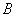 .
.
3) Если события  и
и 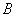 независимы, то по 2) события
независимы, то по 2) события 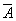 и
и 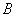 независимы; и по 1)
независимы; и по 1) 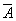 и
и 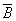 независимы.
независимы.
Определение. События 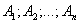 независимы в совокупности, если
независимы в совокупности, если
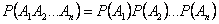 .
.
Определение. События 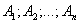 попарно независимы, если в любой паре
попарно независимы, если в любой паре 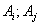 события
события 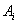 и
и 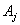 независимы.
независимы.
Независимость в совокупности и попарная независимость событий – понятия разные.
Пример. Три грани треугольной пирамиды окрашены соответственно в белый, зеленый, желтый цвета. На последней грани присутствуют все три цвета. Случайным образом выбирают грань. Найти вероятности событий:  =«на грани есть желтый цвет»;
=«на грани есть желтый цвет»;
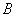 =«на грани есть белый цвет»;
=«на грани есть белый цвет»;
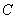 =«на грани есть зеленый цвет»;
=«на грани есть зеленый цвет»;
Решение. Желтый цвет имеется на двух гранях из четырех, т.о. 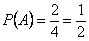 ; аналогично:
; аналогично: 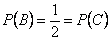 . Вероятность того, что на выпавшей грани есть два цвета -
. Вероятность того, что на выпавшей грани есть два цвета - 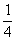 , т.е.
, т.е. 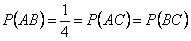 . Таким образом,
. Таким образом,
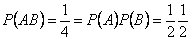
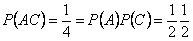
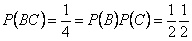 ,
,
Т.е. все события попарно независимы. Однако события не являются независимыми в совокупности:
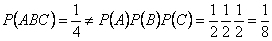
Теорема. (О появлении хотя бы одного из независимых событий)
Пусть вероятность появления каждого из п событий 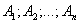 , независимых в совокупности, равна
, независимых в совокупности, равна 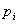 . Вероятность появления хотя бы одного события, равна
. Вероятность появления хотя бы одного события, равна
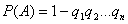 ,
, 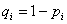
Доказательство. Поскольку по закону Де Моргана
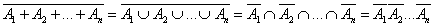 ,
,
то
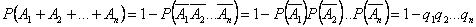 .
.
Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая карта.
Решение. Пусть событие  означает «среди четырех вынутых карт есть хотя бы одна бубновая карта». Тогда
означает «среди четырех вынутых карт есть хотя бы одна бубновая карта». Тогда 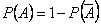 . Событие
. Событие 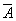 означает, что все четыре карты не бубновой масти. Вероятность того, что случайно взятая из колоды карта не бубновая - и
означает, что все четыре карты не бубновой масти. Вероятность того, что случайно взятая из колоды карта не бубновая - и 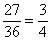 , тогда
, тогда 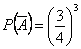 ,
, 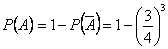
9. Формула полной вероятности и формула Байеса. Пример.
Если событие А может произойти только при выполнении одного из событий 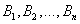 , которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле
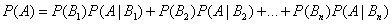 .
.
Эта формула называется формулой полной вероятности.
Вновь рассмотрим полную группу несовместных событий 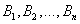 , вероятности появления которых
, вероятности появления которых 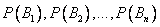 . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий 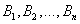 , которые будем называть гипотезами. Тогда по формуле полной вероятности
, которые будем называть гипотезами. Тогда по формуле полной вероятности
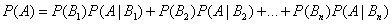
Если событие А произошло, то это может изменить вероятности гипотез 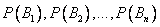 .
.
По теореме умножения вероятностей
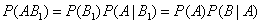 ,
,
откуда
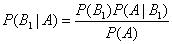 .
.
Аналогично, для остальных гипотез
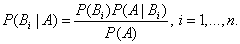
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез 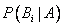 называются апостериорными вероятностями, тогда как
называются апостериорными вероятностями, тогда как 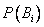 - априорными вероятностями.
- априорными вероятностями.
Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через 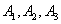 обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
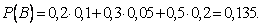
Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Решение. Возможны три гипотезы:
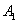 - на линию огня вызван первый стрелок,
- на линию огня вызван первый стрелок,
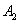 - на линию огня вызван второй стрелок,
- на линию огня вызван второй стрелок,
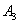 - на линию огня вызван третий стрелок.
- на линию огня вызван третий стрелок.
Так как вызов на линию огня любого стрелка равновозможен, то 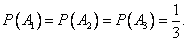
В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
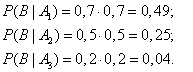
по формуле Байеса находим вероятность гипотезы 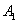 после опыта:
после опыта:
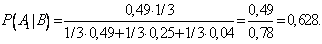
Пример. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.
а) Каков процент брака на конвейере?
б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?
Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: 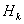 – взятая наудачу деталь обработана на
– взятая наудачу деталь обработана на 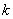 -ом станке,
-ом станке, 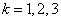 .
.
Условные вероятности (в условии задачи они даны в форме процентов):
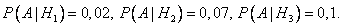
Зависимости между производительностями станков означают следующее:
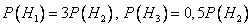 .
.
А так как гипотезы образуют полную группу, то 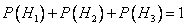 .
.
Решив полученную систему уравнений, найдем: 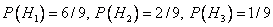 .
.
а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:
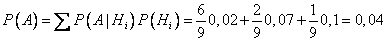 .
.
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.
б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:
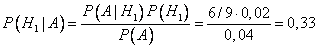 ,
,
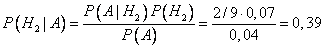 ,
,
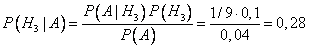 .
.
 Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.
Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.
10. Испытания Бернулли.
Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении nиспытаний событие A появится ровно k раз.
Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в nнезависимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:
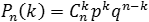
где C n k — число сочетаний, q = 1 − p
Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.
По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию Aпротивопоставляется событие «не A», т.е. выпуск бракованного изделия.
Таким образом, имеем: n = 10; p = 0,8; q = 0,2.
Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):
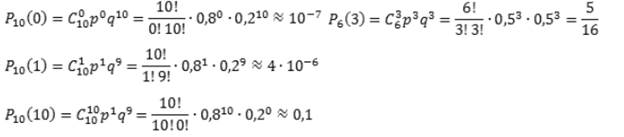
11. Понятие случайной величины. Функция распределения случайной величины.
Понятие случайной величины является одним из основных понятий теории вероятностей. Под данным термином подразумевается величина, значения которой зависят от случая и для которой определена функция распределения вероятностей. Функцией распределения вероятностей случайной величины ξ называется вероятность того, что ξ примет значение, меньшее, чем произвольное число х:
F(x) = P{ξ .
Случайные величины принято обозначать греческими буквами, а принимаемые ими значения – строчными латинскими [23]. В зависимости от характера принимаемых значений различают 2 основных класса случайных величин: дискретные и непрерывные.
Дискретные случайные величины могут принимать только конечное или счетное множество значений. Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределенияданной случайной величины.
Пусть ξ – дискретная случайная величина, единственно возможными значениями которой являются числа x1,x2,...,xn. Обозначим через
pi = P(ξ = xi)(i=1,2,...,n)
вероятности этих значений. Тогда закон распределения случайной величины ξ задает таблица
| ξ | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
Непрерывной называется случайная величина, все возможные значения которой целиком заполняют некоторый конечный или бесконечный промежуток числовой оси. Для любой непрерывной случайной величины существует неотрицательная функция f(x), при любых х удовлетворяющая равенству: F(x)=∫−∞xf(x)dxF(x)=∫−∞xf(x)dx.
Функция f(x) называется плотностью распределения вероятностей непрерывной случайной величины.
Плотность распределения вероятностей обладает следующими свойствами:
1. f(x)≥0.
2. При любых x1 и x2 удовлетворяет равенству P{x1⩽ξ<x2}=∫x1x2f(x)dxP{x1⩽ξ<x2}=∫x1x2f(x)dx.
3. ∫f(x)dx = 1.
F(x) является первообразной функцией для функции f(x):
F'(x) = f(x),
поэтому функцию F(x) называют также интегральным, а плотность вероятностей f(x) - дифференциальным закономраспределения случайной величины ξ. Функция распределения имеет также смысл для дискретных случайных величин.
В теории вероятностей в отношении непрерывных случайных величин доказана следующая важная теорема [27].
Теорема. Вероятность (до опыта) того, что непрерывная случайная величина ξ примет заранее указанное строго определенное значение а, равна нулю.
Рассмотрим теперь вероятностное пространство {Ω, Θ, P}, на котором определены n случайных величин
ξ1 = f1(ω), ξ2 = f2(ω),...,ξn = fn(ω).
Тогда вектор (ξ1,ξ2,...,ξn) называется случайным вектором или n-мерной случайной величиной.
Обозначим через {ξ11,ξ22,...,ξnn} множество тех элементарных событий ω, для которых одновременно выполняются неравенства
ξ11,ξ22,...,ξnn.
Это событие принадлежит множеству Θ, т.е.
{ξ11,ξ22,...,ξnn}∈Θ.
Таким образом, при любом наборе чисел определена вероятность
F(x1,x2,...,xn) = P{ξ11,ξ22,...,ξnn}.
Функция F(x1,x2,...,xn) от n аргументов называется n-мерной функцией распределения случайного вектора (ξ1,ξ2,...,ξn).
Геометрическая интерпретация рассматривает вектор (ξ1,ξ2,...,ξn) как координаты точки n-мерного евклидова пространства. Функция F(x1,x2,...,xn) при такой интерпретации дает вероятность попадания точки (ξ1,ξ2,...,ξn) в n-мерный параллелепипед ξ11,ξ22,...,ξnn с ребрами, параллельными осям координат.
Функция распределения, указывая на то, какие значения может принимать случайная величина и с какими вероятностями, представляет собой наиболее полную характеристику последней. Однако общую количественную характеристику о случайной величине могут дать некоторые постоянные числа, получаемые по определенным правилам из функций распределения. К числу этих постоянных относятся математическое ожидание и дисперсия.
Для произвольной случайной величины ξ с функций распределения f(x) математическим ожиданием называется интеграл
Mξ = ∫xdF(x).
Для непрерывных случайных величин, распределенных по нормальному закону, математическое ожидание равно генеральному среднему, а его наилучшей точечной оценкой является выборочное среднее. Наилучшей точечной оценкой асимметрично распределенных непрерывных случайных величин является медиана.
Дисперсией случайной величины ξ называется математическое ожидание квадрата уклонения ξ от Mξ:
Dξ = M(ξ - Mξ)2.
Таким образом, математическое ожидание представляет собой характеристику центральной тенденции (типичного значения) случайной величины, а дисперсия – меры ее рассеяния.
В заключение следует также охарактеризовать независимые и зависимые случайные величины. Две случайные величины считаются независимыми, если возможные значения и закон распределения каждой из них один и тот же при любом выборе допустимых значений другой. В противном случае случайные величины называются зависимыми. Несколько случайных величин являются взаимно независимыми, если возможные значения и законы распределения любой из них не зависят от того, какие возможные значения приняли остальные случайные величины.
12. Теорема о свойствах функции распределения случайной величины.
Функцией распределения случайной величины 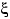 мы назвали функцию
мы назвали функцию 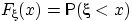 . Основные свойства этой функции заключены в теореме:
. Основные свойства этой функции заключены в теореме:
Теорема 20. Любая функция распределения обладает следующими свойствами:
(F1)
она не убывает: если 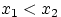 , то
, то 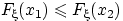 ;
;
(F2)
cуществуют пределы 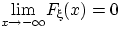 и
и 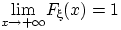 ;
;
(F3)
она в любой точке непрерывна слева: 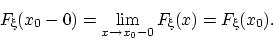
Доказательство свойства (F1). Для любых чисел 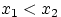 событие
событие 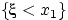 влечёт событие
влечёт событие 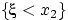 , т.е.
, т.е. 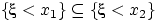 . Но вероятность — монотонная функция событий, поэтому
. Но вероятность — монотонная функция событий, поэтому
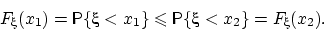
QED
Для доказательства остальных свойств нам понадобится свойство непрерывности вероятностной меры.
Доказательство свойства (F2). Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции 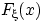 . Остается лишь доказать равенства
. Остается лишь доказать равенства
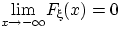 ,
, 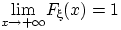 и
и 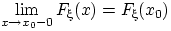 .
.
Для этого в каждом случае достаточно найти предел по какой-нибудь подпоследовательности  , так как существование предела влечёт совпадение всех частичных пределов.
, так как существование предела влечёт совпадение всех частичных пределов.
Докажем, что 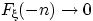 при
при 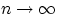 . Рассмотрим вложенную убывающую последовательность событий
. Рассмотрим вложенную убывающую последовательность событий 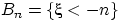 :
:
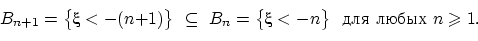
Пересечение 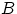 всех этих событий состоит из тех и только тех
всех этих событий состоит из тех и только тех 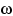 , для которых
, для которых 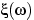 меньше любого вещественного числа. Но для любого элементарного исхода
меньше любого вещественного числа. Но для любого элементарного исхода 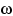 значение
значение 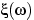 вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий
вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий 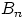 не содержит элементарных исходов, т.е.
не содержит элементарных исходов, т.е. 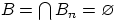 . По свойству непрерывности меры,
. По свойству непрерывности меры, 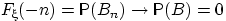 при
при 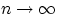 .
.
Точно так же докажем остальные свойства.
Покажем, что 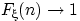 при
при 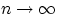 , т.е.
, т.е. 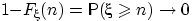 . Обозначим через
. Обозначим через 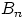 событие
событие 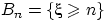 . События
. События 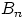 вложены:
вложены:
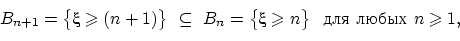
а пересечение 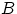 этих событий снова пусто — оно означает, что
этих событий снова пусто — оно означает, что 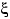 больше любого вещественного числа. По свойству непрерывности меры,
больше любого вещественного числа. По свойству непрерывности меры, 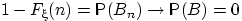 при
при 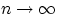 .
.
Доказательство свойства (F3). Достаточно доказать, что 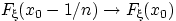 при
при 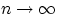 . Иначе говоря, доказать сходимость к нулю следующей разности:
. Иначе говоря, доказать сходимость к нулю следующей разности:
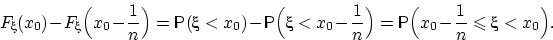
Следующая теорема говорит о том, что три доказанных свойства полностью описывают класс функций распределения. То, что любая функция распределения ими обладает, мы с вами доказали, а теорема утверждает, что любая функция с такими свойствами есть функция распределения.
Теорема 21. Если функция 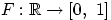 удовлетворяет свойствам (F1)—(F3), то
удовлетворяет свойствам (F1)—(F3), то 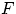 есть функция распределения некоторой случайной величины
есть функция распределения некоторой случайной величины 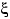 , т.е. найдётся вероятностное пространство
, т.е. найдётся вероятностное пространство 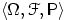 и случайная величина
и случайная величина 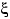 на нём такая, что
на нём такая, что 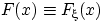 .
.
Эту теорему мы доказывать не станем. Хотя её можно попробовать доказать конструктивно — предъявив то вероятностное пространство (проще всего отрезок 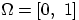 с
с 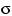 -алгеброй борелевских множеств и мерой Лебега) и ту случайную величину, о существовании которых идёт речь.
-алгеброй борелевских множеств и мерой Лебега) и ту случайную величину, о существовании которых идёт речь.
Помимо отмеченных в теореме 20, функции распределения обладают следующими свойствами:
(F4)
В любой точке 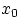 разница
разница 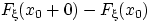 равна
равна 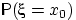 :
:
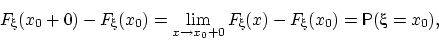
или, иначе говоря, 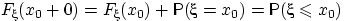 .
.
Заметим, что разница 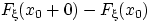 между пределом при стремлении к
между пределом при стремлении к 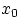 справа и значением в точке
справа и значением в точке 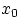 есть величина скачка функции распределения. Эта величина равна нулю, если функция распределения непрерывна (справа) в точке
есть величина скачка функции распределения. Эта величина равна нулю, если функция распределения непрерывна (справа) в точке 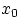 . Слева функция распределения непрерывна всегда.
. Слева функция распределения непрерывна всегда.
Замечание 13. Очень часто функцией распределения называют 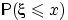 . Эта функция отличается от определённой выше лишь тем, что она непрерывна справа, а не слева. Соответственно, вероятность
. Эта функция отличается от определённой выше лишь тем, что она непрерывна справа, а не слева. Соответственно, вероятность 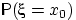 для неё равна величине скачка слева, а не справа.
для неё равна величине скачка слева, а не справа.
(F5)
Для любой случайной величины 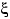 имеет место равенство:
имеет место равенство:
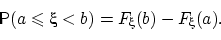
| (13) |
Если же функция распределения 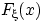 непрерывна в точках
непрерывна в точках 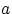 и
и 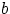 , то
, то
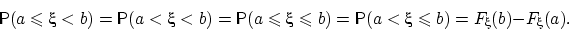
Доказательство. Докажем только равенство (13). Все остальные равенства следуют из него и свойства (F4).
Заметим, что 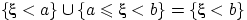 , и первые два события несовместны. Поэтому
, и первые два события несовместны. Поэтому 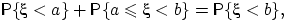 или
или 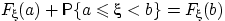 , что и требовалось доказать.
, что и требовалось доказать.
13. Понятие дискретной случайной величины. Ряд и многоугольник распределения. Пример.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Примеры
Проще говоря, дискретные случайные величины — это величины, количество значений которых можно пересчитать. Например:
1. Число попаданий в мишень при nn выстрелах. Принимаемые значения 0…n0…n
2. Количество выпавших орлов при nn бросков монетки. Принимаемые значения 0…n0…n
3. Число очков, выпавших при бросании игральной кости. Случайная величина принимает одно из значений — {1,2,3,4,5,6}{1,2,3,4,5,6}
Существуют также непрерывные случайные величины. Например, координаты точки попадания при выстреле.
Рассмотрим прерывную случайную величину  с возможными значениями
с возможными значениями 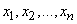 . Каждое из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью. В результате опыта величина Х примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий:
. Каждое из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью. В результате опыта величина Х примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий:
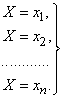 (5.1.1)
(5.1.1)
Обозначим вероятности этих событий буквами p с соответствующими индексами:
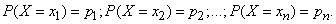
Так как несовместные события (5.1.1) образуют полную группу, то
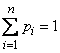 ,
,
т.е. сумма вероятностей всех возможных значений случайной величины равна единице. Эта суммарная вероятностькаким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое из событий (5.1.1). Этим мы установим так называемый закон распределения случайной величины.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину мы будем говорить, что она подчинена данному закону распределения.
Установим форму, в которой может быть задан закон распределения прерывной случайной величины  . Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:
. Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:
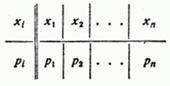
Такую таблицу мы будем называть рядом распределения случайной величины  .
.
Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Для наглядности полученные точки соединяются отрезками прямых. Такая фигура называется многоугольником распределения (рис. 5.1.1). Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную величину; он является одной из форм закона распределения.
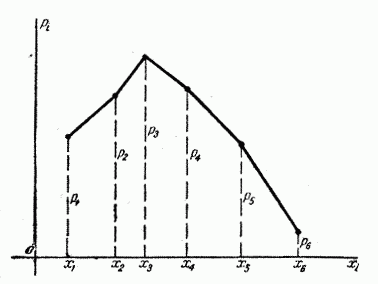
Рис. 5.1.1.
Иногда удобной оказывается так называемая «механическая» интерпретация ряда распределения. Представим себе, что некоторая масса, равная единице, распределена по оси абсцисс так, что в 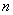 отдельных точках
отдельных точках 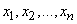 сосредоточены соответственно массы
сосредоточены соответственно массы 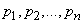 . Тогда ряд распределения интерпретируется как система материальных точек с какими-то массами, расположенных на оси абсцисс.
. Тогда ряд распределения интерпретируется как система материальных точек с какими-то массами, расположенных на оси абсцисс.
Рассмотрим несколько примеров прерывных случайных величин с их законами распределения.
Пример 1. Производится один опыт, в котором может появиться или не появиться событие  . Вероятность события
. Вероятность события  равна 0,3. Рассматривается случайная величина
равна 0,3. Рассматривается случайная величина  – число появлений события
– число появлений события  в данном опыте (т.е. характеристическая случайная величина события
в данном опыте (т.е. характеристическая случайная величина события  , принимающая значение 1, если оно появится, и 0, если не появится). Построить ряд распределения и многоугольник распределения величины
, принимающая значение 1, если оно появится, и 0, если не появится). Построить ряд распределения и многоугольник распределения величины  .
.
Решение. Величина  имеет всего два значения: 0 и 1. Ряд распределения величины
имеет всего два значения: 0 и 1. Ряд распределения величины  имеет вид:
имеет вид:
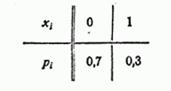
Многоугольник распределения изображен на рис. 5.1.2.
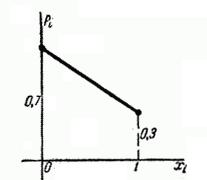
Рис. 5.1.2.
Пример 2. Стрелок производит три выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывается 5 очков. Построить ряд распределения числа выбитых очков.
Решение. Обозначим  число выбитых очков. Возможные значения величины
число выбитых очков. Возможные значения величины  :
: 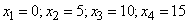 .
.
Вероятность этих значений находим по теореме о повторении опытов:
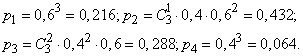
Ряд распределения величины  имеет вид:
имеет вид:

Многоугольник распределения изображен на рис. 5.1.3.
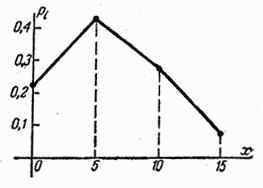
Рис. 5.1.3.
Пример 3. Вероятность появления события  в одном опыте равна
в одном опыте равна 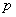 . Производится ряд независимых опытов, которые продолжаются до первого появления события
. Производится ряд независимых опытов, которые продолжаются до первого появления события  , после чего опыты прекращаются. Случайная величина
, после чего опыты прекращаются. Случайная величина  – число произведенных опытов. Построить ряд распределения величины
– число произведенных опытов. Построить ряд распределения величины  .
.
Решение. Возможные значения величины  : 1, 2, 3, … (теоретически они ничем не ограничены). Для того, чтобы величина
: 1, 2, 3, … (теоретически они ничем не ограничены). Для того, чтобы величина  приняла значение 1, необходимо, чтобы событие
приняла значение 1, необходимо, чтобы событие  произошло в первом же опыте; вероятность этого равна
произошло в первом же опыте; вероятность этого равна 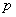 . Для того, чтобы величина
. Для того, чтобы величина  приняла значение 2, нужно, чтобы в первом опыте событие
приняла значение 2, нужно, чтобы в первом опыте событие  не появилось, а во втором – появилось; вероятность этого равна
не появилось, а во втором – появилось; вероятность этого равна 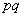 , где
, где 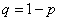 , и т.д. Ряд распределения величины
, и т.д. Ряд распределения величины  имеет вид:
имеет вид:
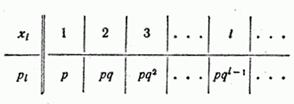
Первые пять ординат многоугольника распределения для случая 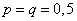 показаны на рис. 5.1.4.
показаны на рис. 5.1.4.
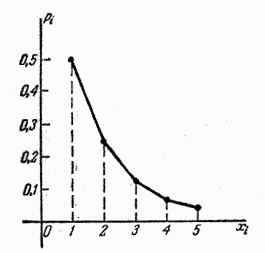
Рис. 5.1.4.
Пример 4. Стрелок ведет стрельбу по мишени до первого попадания, имея боезапас 4 патрона. Вероятностьпопадания при каждом выстреле равна 0,6. Построить ряд распределения боезапаса, оставшегося неизрасходованным.
Решение. Случайная величина  – число неизрасходованных патронов – имеет четыре возможных значения: 0, 1, 2 и 3. Вероятности этих значений равны соответственно:
– число неизрасходованных патронов – имеет четыре возможных значения: 0, 1, 2 и 3. Вероятности этих значений равны соответственно:
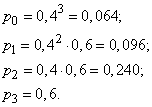
Ряд распределения величины  имеет вид:
имеет вид:

Многоугольник распределения показан на рис. 5.1.5.
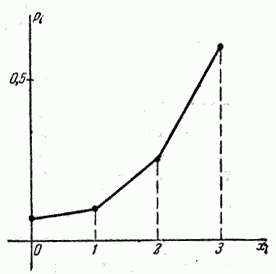
Рис. 5.1.5.
14. Теорема о свойствах функции распределения дискретной случайной величины.
если x - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
| x1 | x2 | … | xi | … |
| p1 | p2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
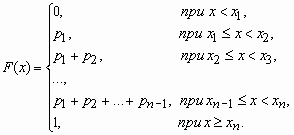
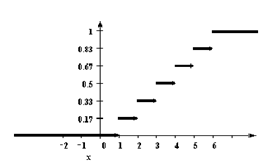
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |


15. Понятие непрерывной случайной величины. Плотность и функция распределения.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.
| |||||||||||||||
| Если рассматривать случайную величину Х, значения которой заполняют интервал (a,b) и составить перечень всех возможных её значений невозможно, то она называется непрерывной. В результате этого появилась необходимость дать общий способ задания любых типов случайных величин. Для этого вводится функция распределения вероятностей случайной величины. Функция распределения F(х) для непрерывной случайной величины имеет вид:
где: f(х) – функция плотности вероятности вычисляется по формуле:
Функцию распределения F(х) называют интегральным законом распределения, плотность вероятности f(х). называют дифференциальным законом распределения. Свойства функции распределения F(х): Свойство 1. Значения функции распределения F(х) принадлежат отрезку [0, 1]: 0 £ F(х) £ 1. Свойство 2. F(х) – неубывающая функция: F ( х1 ) £ F( х2 ), если х1< х2. Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) равна приращению функции распределения на этом интервале: Р (а £ Х <b) = F(b) – F(а). Свойство 3.Если возможные значения случайной величины принадлежат интервалу (a,b), то: F(x)=0 при x£a; F(x)=1 при x³b. Следствие 2. Если возможные значения непрерывной случайной величины расположены на всей оси х, то:
Свойства плотности вероятности f(х) : Свойство 1. Плотность вероятности не может быть отрицательной: f(х) ³ 0. Свойство 2.
Следствие. В частности, если значения случайной величины находятся в интервале (a, b), то вероятность попадания в заданный интервал
Функция распределения связана с плотностью формулой:
| |||||||||||||||
16. Теорема о свойствах плотности распределения непрерывной случайной величины.

Случайная величина Х называется непрерывной, если ее функция распределения F(x) есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Так как для таких случайных величин функция F(x) нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю
P{X=α}=0 для любого α.
В качестве закона распределения, имеющего смысл только для непрерывных случайных величин существует понятие плотности распределения или плотности вероятности.
Вероятность попадания непрерывной случайной величины X на участок от x до x+Dx равна приращению функции распределения на этом участке:
P{x£ X <x+Dx}=F(x+Dx) - F(x).
Плотность вероятности на этом участке определяется отношением
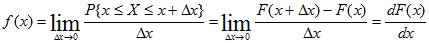 (5.6)
(5.6)
Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.
Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Эта величина называется элементом вероятности.
Вероятность попадания случайной величины X на произвольный участок [a, b[ равна сумме элементарных вероятностей на этом участке:
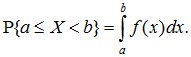 (5.7)
(5.7)
В геометрической интерпретации P{α≤X<β} равна площади, ограниченной сверху кривой плотности распределения f(x) и опирающейся на участок (α,β) (рис. 5.4).
Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:
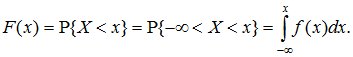 (5.8)
(5.8)
В геометрической интерпретации F(x) равна площади, ограниченной сверху кривой плотности распределения f(x) и лежащей левее точки x (рис. 5.5).
Основные свойства плотности распределения:
- Плотность распределения неотрицательна: f(x) ³ 0.
Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной.
2. Условие нормировки: 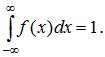 Это свойство следует из формулы (5.8), если положить в ней x=∞.
Это свойство следует из формулы (5.8), если положить в ней x=∞.
Геометрически основные свойства плотности f(x) интерпретируются так:
- вся кривая распределения лежит не ниже оси абсцисс;
- полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
17. Математическое ожидание случайной величины и его свойства.
18. Дисперсия случайной величины и её свойства.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
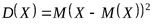 .
.
Слово «дисперсия» означает «рассеяние», т.е. дисперсия характеризует рассеяние (разбросанность) значений случайной величины около ее математического ожидания.
Из определения следует, что дисперсия – это постоянная величина, т.е. числовая характеристика случайной величины, которая имеет размерность квадрата случайной величины.
С вероятной точки зрения, дисперсия является мерой рассеяния значений случайной величины около ее математического ожидания.
Действительно, рассмотрим дискретную случайную величину, которая имеет конечное множество значений. Тогда, согласно определению, дисперсия вычисляется по формуле
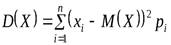 . (2)
. (2)
Если дисперсия 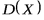 мала, то из формулы (2) следует, что малы слагаемые
мала, то из формулы (2) следует, что малы слагаемые 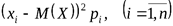 . Поэтому, если не рассматривать значения
. Поэтому, если не рассматривать значения 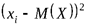 , которым соответствует малая вероятность (такие значения практически невозможны), то все остальные значения
, которым соответствует малая вероятность (такие значения практически невозможны), то все остальные значения 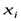 мало отклоняются от математического ожидания
мало отклоняются от математического ожидания 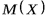 . Следовательно,при малой дисперсии возможные значения случайной величины концентрируются около ее математического ожидания (за исключением, может быть, сравнительно малого числа отдельных значений). Если дисперсия
. Следовательно,при малой дисперсии возможные значения случайной величины концентрируются около ее математического ожидания (за исключением, может быть, сравнительно малого числа отдельных значений). Если дисперсия 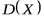 велика, то это означает большой разброс значений случайной величины, концентрация значений случайной величины около какого-нибудь центра исключается.
велика, то это означает большой разброс значений случайной величины, концентрация значений случайной величины около какого-нибудь центра исключается.
Пример. Пусть случайные величины 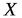 и
и 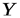 имеют следующее законы распределения
имеют следующее законы распределения
Таблица 9. Таблица 10.
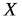
| -0,1 | 0 | 0,1 | 0,4 | 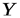
| -10 | 0,5 | 10 | |
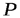
| 0,3 | 0,15 | 0,3 | 0,25 | 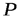
| 0,4 | 0,2 | 0,4 |
Найти математические ожидания и дисперсии этих случайных величин.
Решение. Воспользовавшись формулой для вычисления математических ожиданий, находим
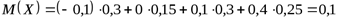 .
.
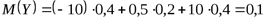 .
.
С помощью формулы (2) вычислим дисперсии заданных случайных величин
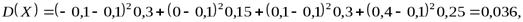
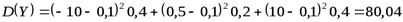 .
.
Из полученных результатов делаем вывод: математические ожидания случайных величин 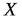 и
и 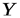 одинаковы, однако дисперсии различны. Дисперсия случайной величины
одинаковы, однако дисперсии различны. Дисперсия случайной величины 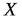 мала и мы видим, что ее значение сконцентрированы около ее математического ожидания
мала и мы видим, что ее значение сконцентрированы около ее математического ожидания 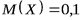 . Напротив, значения случайной величины
. Напротив, значения случайной величины 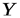 значительно рассеяны относительно
значительно рассеяны относительно 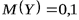 , а поэтому дисперсия
, а поэтому дисперсия 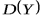 имеет большое значение. ●
имеет большое значение. ●
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины равна нулю
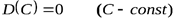 .
.
Доказательство.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат
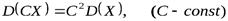 .
.
Доказательство.
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий
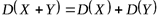 .
.
Доказательство. Воспользуемся определением дисперсии и свойствами 3, 2 математического ожидания, имеем
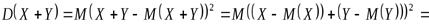
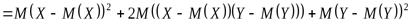 (3)
(3)
Определение. Математическое ожидание произведения отклонений случайных величин  и
и  от их математических ожиданий называетсякорреляционным моментом этих величин
от их математических ожиданий называетсякорреляционным моментом этих величин
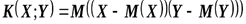 .
.
Если случайные величины, величины 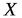 и
и 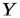 независимы, то, воспользовавшись свойствами 6 и 7 математических ожиданий, находим
независимы, то, воспользовавшись свойствами 6 и 7 математических ожиданий, находим
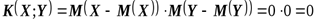 .
.
Поэтому из формулы 3 имеем
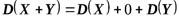 ,
,
откуда окончательно следует
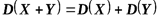 . ●
. ●
С помощью метода математической индукции это свойство может быть распространено на случай любого конечного числа независимых случайных величин.
Свойство 4. Дисперсия суммы независимых случайных величин 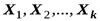 равна сумме их дисперсий
равна сумме их дисперсий
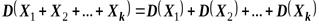 . ●
. ●
Свойство 5. Дисперсия разности двух случайных независимых величин равна сумме дисперсий этих величин
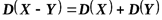 .
.
Доказательство.
Свойство 6. Дисперсия случайной величины равна математическому ожиданию
квадрата этой величины минус квадрат ее математического ожидания
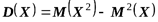 .
.
(Эта формула применяется для вычисления дисперсии)
19. Понятия центрированной и нормированной случайных величин, их числовые характеристики.

математическое ожидание центрированной случайной величины всегда равно нулю.
Здесь есть этот математический бред - http://sernam.ru/book_tp.php?id=22
20. Биномиальный закон распределения.
Обычно нас интересует лишь общее число успехов, достигнутых в последовательности из n испытаний Бернулли, а не порядок следования успехов. В этом смысле мы не делаем различий между событиями, состоящими, например, из последовательностей
{У, У, У, Н, Н}, {У, У, Н, У, Н}, {У, У, Н, Н, У}, {У, Н, У, У, Н} и т.д.
Событие “n испытаний привели m раз к успеху” содержит столько элементарных событий, сколькими способами можно распределить m символов по n местам, что совпадает с числом сочетаний 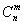 из nэлементов по m.
из nэлементов по m.
Другими словами, пространство элементарных событий состоит из  точек, каждая из которых, по определению, имеет вероятность
точек, каждая из которых, по определению, имеет вероятность 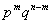 .
.
Следовательно, вероятность m успехов ( 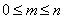 ) в серии из n испытаний Бернулли описывается формулой
) в серии из n испытаний Бернулли описывается формулой
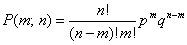 , (*)
, (*)
где p – вероятность успеха; q – вероятность неудачи в одном испытании (q = 1 – р).
Согласно существующей терминологии, число успехов в серии из n испытаний является случайной величиной, а формула (*) описывает распределение этой случайной величины и называется биномиальным законом распределения вероятности.
Заметим, что выражение 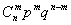 представляет собой m-ый член биномиального разложения
представляет собой m-ый член биномиального разложения 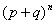 .
.
Следовательно,
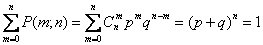 ,
,
как того и требует понятие вероятности.
Выражение, содержащее произведение вида 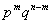 , представляет собой вероятность m успехов в серии из n испытаний Бернулли:
, представляет собой вероятность m успехов в серии из n испытаний Бернулли:
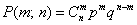 .
.
Заметим, что события
– 0 успехов,
– 1 успех,
– 2 успеха,
– …,
– n успехов в серии из n испытаний Бернулли
образуют полную группу событий, поскольку они попарно несовместимы и вместе образуют достоверное событие.
Частные случаи.
– Вероятность того, что в серии из n испытаний успех не наступит ни разу, равна 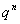 .
.
– Вероятность наступления хотя бы одного успеха в серии из n испытаний равна
 (**)
(**)
21. 
 Закон распределения Пуассона.
Закон распределения Пуассона.
Математический бред и примеры:
Рассмотрим прерывную случайную величину  , которая может принимать только целые, неотрицательные значения:
, которая может принимать только целые, неотрицательные значения:
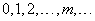 ,
,
причем последовательность этих значений теоретически не ограничена.
Говорят, что случайная величина  распределена по закону Пуассона, если вероятность того, что она примет определенное значение
распределена по закону Пуассона, если вероятность того, что она примет определенное значение 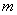 , выражается формулой
, выражается формулой
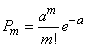
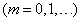 , (5.9.1)
, (5.9.1)
где а – некоторая положительная величина, называемая параметром закона Пуассона.
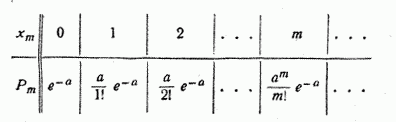
Ряд распределения случайной величины  , распределенной по закону Пуассона, имеет вид:
, распределенной по закону Пуассона, имеет вид:
Убедимся, прежде всего, что последовательность вероятностей, задаваемая формулой (5.9.1), может представлять собой ряд распределения, т.е. что сумма всех вероятностей  равна единице. Имеем:
равна единице. Имеем:
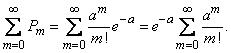
Но
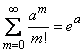 ,
,
откуда
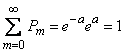 .
.
На рис. 5.9.1 показаны многоугольники распределения случайной величины  , распределенной по закону Пуассона, соответствующие различным значениям параметра
, распределенной по закону Пуассона, соответствующие различным значениям параметра  . В таблице 8 приложения приведены значения
. В таблице 8 приложения приведены значения  для различных
для различных 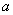 .
.
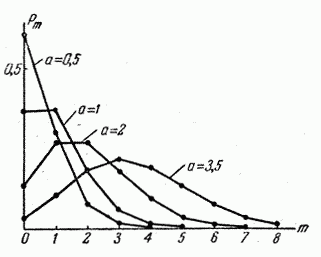
Рис. 5.9.1.
Определим основные характеристики – математическое ожидание и дисперсию – случайной величины  , распределенной по закону Пуассона. По определению математического ожидания
, распределенной по закону Пуассона. По определению математического ожидания
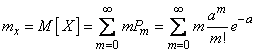 .
.
Первый член суммы (соответствующий 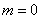 ) равен нулю, следовательно, суммирование можно начать с
) равен нулю, следовательно, суммирование можно начать с 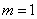 :
:
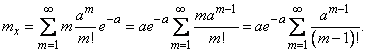
Обозначим 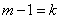 ; тогда
; тогда
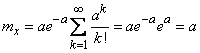 . (5.9.2)
. (5.9.2)
Таким образом, параметр 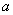 представляет собой не что иное, как математическое ожидание случайной величины
представляет собой не что иное, как математическое ожидание случайной величины  .
.
Для определения дисперсии найдем сначала второй начальный момент величины  :
:
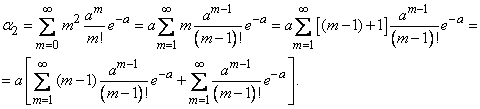
По ранее доказанному
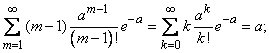
кроме того,
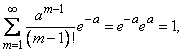
следовательно,
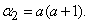
Далее находим дисперсию величины  :
:
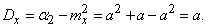 (5.9.3)
(5.9.3)
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна её математическому ожиданию 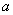 .
.
Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина  распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики – математическое ожидание и дисперсию – случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
Определим для случайной величины  , распределенной по закону Пуассона, вероятность того, что она примет значение не меньше заданного
, распределенной по закону Пуассона, вероятность того, что она примет значение не меньше заданного 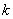 . Обозначим эту вероятность
. Обозначим эту вероятность 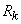 :
:
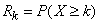 .
.
Очевидно, вероятность 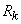 может быть вычислена как сумма
может быть вычислена как сумма
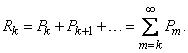
Однако значительно проще определить её из вероятности противоположного события:
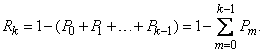 (5.9.4)
(5.9.4)
В частности, вероятность того, что величина  примет положительное значение, выражается формулой
примет положительное значение, выражается формулой
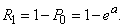 (5.9.5)
(5.9.5)
Мы уже упоминали о том, что многие задачи практики приводят к распределению Пуассона. Рассмотрим одну из типичных задач такого рода.

Рис. 5.9.2.
Пусть на оси абсцисс Ох случайным образом распределяются точки (рис. 5.9.2). Допустим, что случайное распределение точек удовлетворяет следующим условиям:
1. Вероятность попадания того или иного числа точек на отрезок  зависит только от длины этого отрезка, но не зависит от его положения на оси абсцисс. Иными словами, точки распределяются на оси абсцисс с одинаковой средней плотностью. Обозначим эту плотность (т.е. математическое ожидание числа точек, приходящихся на единицу длины) через
зависит только от длины этого отрезка, но не зависит от его положения на оси абсцисс. Иными словами, точки распределяются на оси абсцисс с одинаковой средней плотностью. Обозначим эту плотность (т.е. математическое ожидание числа точек, приходящихся на единицу длины) через  .
.
2. Точки распределяются на оси абсцисс независимо друг от друга, т.е. вероятность попадания того или другого числа точек на заданный отрезок не зависит от того, сколько их попало на любой другой отрезок, не перекрывающийся с ним.
3. Вероятность попадания на малый участок 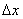 двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).
двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки (это условие означает практическую невозможность совпадения двух или более точек).
Выделим на оси абсцисс определенный отрезок длины 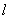 и рассмотрим дискретную случайную величину
и рассмотрим дискретную случайную величину  – число точек, попадающих на этот отрезок. Возможные значения величины будут
– число точек, попадающих на этот отрезок. Возможные значения величины будут
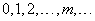 (5.9.6)
(5.9.6)
Так как точки попадают на отрезок независимо друг от друга, то теоретически не исключено, что их там окажется сколь угодно много, т.е. ряд (5.9.6) продолжается неограниченно.
Докажем, что случайная величина  имеет закон распределения Пуассона. Для этого вычислим вероятность
имеет закон распределения Пуассона. Для этого вычислим вероятность 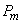 того, что на отрезок
того, что на отрезок 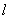 попадет ровно
попадет ровно 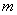 точек.
точек.
Сначала решим более простую задачу. Рассмотрим на оси Ох малый участок 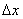 и вычислим вероятность того, что на этот участок попадет хотя бы одна точка. Будем рассуждать следующим образом. Математическое ожиданиечисла точек, попадающих на этот участок, очевидно, равно
и вычислим вероятность того, что на этот участок попадет хотя бы одна точка. Будем рассуждать следующим образом. Математическое ожиданиечисла точек, попадающих на этот участок, очевидно, равно 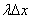 (т.к. на единицу длины попадает в среднем
(т.к. на единицу длины попадает в среднем 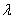 точек). Согласно условию 3 для малого отрезка
точек). Согласно условию 3 для малого отрезка 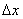 можно пренебречь возможностью попадания на него двух или больше точек. Поэтому математическое ожидание
можно пренебречь возможностью попадания на него двух или больше точек. Поэтому математическое ожидание 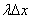 числа точек, попадающих на участок
числа точек, попадающих на участок 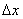 , будет приближенно равно вероятности попадания на него одной точки (или, что в наших условиях равнозначно, хотя бы одной).
, будет приближенно равно вероятности попадания на него одной точки (или, что в наших условиях равнозначно, хотя бы одной).
Таким образом, с точностью до бесконечно малых высшего порядка, при 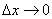 можно считать вероятность того, что на участок
можно считать вероятность того, что на участок 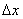 попадет одна (хотя бы одна) точка, равной
попадет одна (хотя бы одна) точка, равной 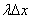 , а вероятность того, что не попадет ни одной, равной
, а вероятность того, что не попадет ни одной, равной 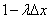 .
.
Воспользуемся этим для вычисления вероятности 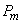 попадания на отрезок
попадания на отрезок 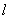 ровно
ровно 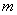 точек. Разделим отрезок
точек. Разделим отрезок 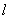 на
на 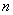 равных частей длиной
равных частей длиной 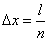 . Условимся называть элементарный отрезок
. Условимся называть элементарный отрезок 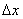 «пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно вышедоказанному вероятностьтого, что отрезок
«пустым», если в него не попало ни одной точки, и «занятым», если в него попала хотя бы одна. Согласно вышедоказанному вероятностьтого, что отрезок 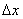 окажется «занятым», приближенно равна
окажется «занятым», приближенно равна 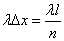 ; вероятность того, что он окажется «пустым», равна
; вероятность того, что он окажется «пустым», равна 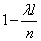 . Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n отрезков можно рассмотреть как
. Так как, согласно условию 2, попадания точек в неперекрывающиеся отрезки независимы, то наши n отрезков можно рассмотреть как 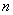 независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью
независимых «опытов», в каждом из которых отрезок может быть «занят» с вероятностью 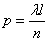 . Найдем вероятность того, что среди
. Найдем вероятность того, что среди 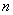 отрезков будет ровно
отрезков будет ровно 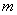 «занятых». По теореме о повторении опытов эта вероятность равна
«занятых». По теореме о повторении опытов эта вероятность равна
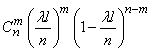
или, обозначая 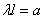 ,
,
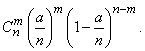 (5.9.7)
(5.9.7)
При достаточно большом  эта вероятность приближенно равна вероятности попадания на отрезок
эта вероятность приближенно равна вероятности попадания на отрезок  ровно
ровно  точек, так как попадание двух или больше точек на отрезок
точек, так как попадание двух или больше точек на отрезок 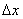 имеет пренебрежимо малую вероятность. Для того чтобы найти точное значение
имеет пренебрежимо малую вероятность. Для того чтобы найти точное значение 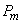 , нужно в выражении (5.9.7) перейти к пределу при
, нужно в выражении (5.9.7) перейти к пределу при 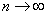 :
:
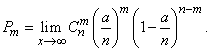 (5.9.8)
(5.9.8)
Преобразуем выражение, стоящее под знаком предела:
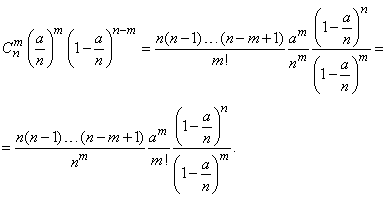 (5.9.9)
(5.9.9)
Первая дробь и знаменатель последней дроби в выражении (5.9.9) при 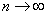 , очевидно, стремятся к единице. Выражение
, очевидно, стремятся к единице. Выражение 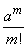 от
от  не зависит. Числитель последней дроби можно преобразовать так:
не зависит. Числитель последней дроби можно преобразовать так:
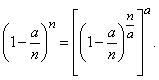 (5.9.10)
(5.9.10)
При 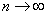
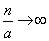 и выражение (5.9.10) стремится к
и выражение (5.9.10) стремится к 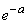 . Таким образом, доказано, что вероятность попадания ровно
. Таким образом, доказано, что вероятность попадания ровно 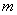 точек в отрезок
точек в отрезок 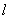 выражается формулой
выражается формулой
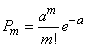 ,
,
где 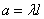 , т.е. величина Х распределена по закону Пуассона с параметром
, т.е. величина Х распределена по закону Пуассона с параметром 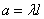 .
.
Отметим, что величина 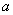 по смыслу представляет собой среднее число точек, приходящееся на отрезок
по смыслу представляет собой среднее число точек, приходящееся на отрезок 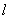 .
.
Величина 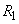 (вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок
(вероятность того, что величина Х примет положительное значение) в данном случае выражает вероятность того, что на отрезок 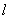 попадет хотя бы одна точка:
попадет хотя бы одна точка:
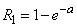 . (5.9.11)
. (5.9.11)
Таким образом, мы убедились, что распределение Пуассона возникает там, где какие-то точки (или другие элементы) занимают случайное положение независимо друг от друга, и подсчитывается количество этих точек, попавших в какую-то область. В нашем случае такой «областью» был отрезок 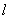 на оси абсцисс. Однако наш вывод легко распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
на оси абсцисс. Однако наш вывод легко распространить и на случай распределения точек на плоскости (случайное плоское поле точек) и в пространстве (случайное пространственное поле точек). Нетрудно доказать, что если соблюдены условия:
1) точки распределены в поле статистически равномерно со средней плотностью 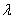 ;
;
2) точки попадают в неперекрывающиеся области независимым образом;
3) точки появляются поодиночке, а не парами, тройками и т.д., то число точек  , попадающих в любую область
, попадающих в любую область 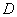 (плоскую или пространственную), распределяются по закону Пуассона:
(плоскую или пространственную), распределяются по закону Пуассона:
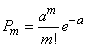
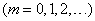 ,
,
где 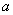 – среднее число точек, попадающих в область
– среднее число точек, попадающих в область 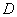 .
.
Для плоского случая
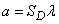 ,
,
где 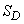 – площадь области
– площадь области 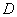 ; для пространственного
; для пространственного
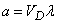 ,
,
где 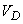 - объем области
- объем области 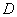 .
.
Заметим, что для пуассоновского распределения числа точек, попадающих в отрезок или область, условие постоянной плотности ( 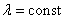 ) несущественно. Если выполнены два других условия, то закон Пуассона все равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножение плотности
) несущественно. Если выполнены два других условия, то закон Пуассона все равно имеет место, только параметр а в нем приобретает другое выражение: он получается не простым умножение плотности 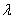 на длину, площадь или объем области, а интегрированием переменной плотности по отрезку, площади или объему. (Подробнее об этом см. n° 19.4)
на длину, площадь или объем области, а интегрированием переменной плотности по отрезку, площади или объему. (Подробнее об этом см. n° 19.4)
Наличие случайных точек, разбросанных на линии, на плоскости или объеме – неединственное условие, при котором возникает распределение Пуассона. Можно, например, доказать, что закон Пуассона является предельным для биномиального распределения:
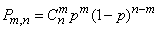 , (5.9.12)
, (5.9.12)
если одновременно устремлять число опытов 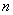 к бесконечности, а вероятность
к бесконечности, а вероятность 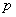 – к нулю, причем их произведение
– к нулю, причем их произведение 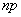 сохраняет постоянное значение:
сохраняет постоянное значение:
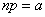 . (5.9.13)
. (5.9.13)
Действительно, это предельное свойство биномиального распределения можно записать в виде:
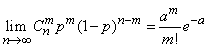 . (5.9.14)
. (5.9.14)
Но из условия (5.9.13) следует, что
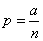 . (5.9.15)
. (5.9.15)
Подставляя (5.9.15) в (5.9.14), получим равенство
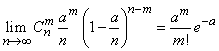 , (5.9.16)
, (5.9.16)
которое только что было доказано нами по другому поводу.
Это предельное свойство биномиального закона часто находит применение на практике. Допустим, что производится большое количество независимых опытов 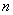 , в каждом из которых событие
, в каждом из которых событие  имеет очень малуювероятность
имеет очень малуювероятность 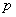 . Тогда для вычисления вероятности
. Тогда для вычисления вероятности 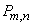 того, что событие
того, что событие  появится ровно
появится ровно 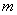 раз, можно воспользоваться приближенной формулой:
раз, можно воспользоваться приближенной формулой:
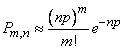 , (5.9.17)
, (5.9.17)
где 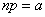 - параметр того закона Пуассона, которым приближенно заменяется биномиальное распределение.
- параметр того закона Пуассона, которым приближенно заменяется биномиальное распределение.
От этого свойства закона Пуассона – выражать биномиальное распределение при большом числе опытов и малой вероятности события – происходит его название, часто применяемое в учебниках статистики: закон редких явлений.
Рассмотрим несколько примеров, связанных с пуассоновским распределением, из различных областей практики.
Пример 1. На автоматическую телефонную станцию поступают вызовы со средней плотностью 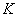 вызовов в час. Считая, что число вызовов на любом участке времени распределено по закону Пуассона, найти вероятность того, что за две минуты на станцию поступит ровно три вызова.
вызовов в час. Считая, что число вызовов на любом участке времени распределено по закону Пуассона, найти вероятность того, что за две минуты на станцию поступит ровно три вызова.
Решение. Среднее число вызовов за две минуты равно:
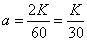 .
.
По формуле (5.9.1) вероятность поступления ровно трех вызовов равна:
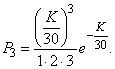
Пример 2. В условиях предыдущего примера найти вероятность того, что за две минуты придет хотя бы один вызов.
Решение. По формуле (5.9.4) имеем:
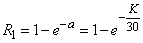 .
.
22. Равномерный закон распределения.
23. Показательный закон распределения.
24. Нормальный закон распределения.
25. Понятие системы случайных величин. Функция совместного распределения системы случайных величин.
26. Теорема о свойствах функции совместного распределения системы двух случайных величин
27. (б/д).
28. Понятие системы двух дискретных случайных величин. Матрица и функция совместного распределения.
29. Частные распределения дискретных случайных величин, входящих в систему.
30. Условные распределения дискретных случайных величин, входящих в систему. Условное математическое ожидание дискретной случайной величины.
31. Корреляционный момент и коэффициент корреляции системы двух дискретных случайных величин.
32. Независимость и некоррелированность случайных величин.
33. Понятия генеральной совокупности и случайной выборки. Пример.
34. Дискретные вариационные ряды. Пример.
35. Интервальные вариационные ряды. Пример.
36. Эмпирическая функция распределения в случае малого объема выборки.
37. Эмпирическая функция распределения в случае большого объема выборки.
38. Полигон и гистограмма.
39. Понятие точечной оценки параметра распределения и её свойства.
40. Метод выборочных моментов точечного оценивания параметров распределения . Пример
41. Метод наименьших квадратов точечного оценивания параметров распределения. Пример.
42. Точечное оценивание генеральной средней.
43. Точечное оценивание генеральной дисперсии.
44. Понятие интервального оценивания параметров распределения. Доверительная вероятность .
45. Интервальное оценивание генеральной средней.
46. Интервальное оценивание генеральной дисперсии.
47. Постановка задачи проверки статистических гипотез.
48. Проверка гипотез о равенстве средних двух совокупностей.
49. Проверка гипотез о равенстве долей двух совокупностей.
50. Проверка гипотез о числовых значениях параметров.
51. Критерий Пирсона проверки гипотез о законе распределения.
52. Критерий Колмогорова проверки гипотез о законе распределения.
53. Теоретическое и выборочное уравнения линейной парной регрессии. Нахождение выборочных параметров линейной парной регрессии.
54. Точечное и интервальное оценивание выборочных параметров линейной парной регрессии









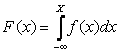 ,
,
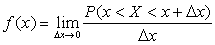 .
.
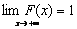 ;
; 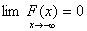 .
.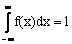 .
.
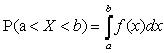 .
.
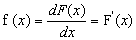 .
.