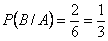Классическое определение

Дата: 2025-05-25; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Классическое «определение» вероятности исходит из понятия равновозможности как объективного свойства изучаемых явлений. Равновозможность является неопределяемым понятием и устанавливается из общих соображений симметрии изучаемых явлений. Например, при подбрасывании монетки исходят из того, что в силу предполагаемой симметрии монетки, однородности материала и случайности (непредвзятости) подбрасывания нет никаких оснований для предпочтения «решки» перед «орлом» или наоборот, то есть выпадение этих сторон можно считать равновозможными (равновероятными).

Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идет об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел.

Классическое определение вероятности можно сформулировать следующим образом:

Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:

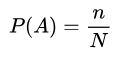
Свойство 1. Вероятность достоверного события равна единице
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Итак, вероятность любого события удовлетворяет двойному неравенству 0≤P(A)≤1

Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно 36 (так как на каждый из 6 возможных исходов одной кости возможно по 6 вариантов исхода другой). Оценим вероятность выпадения семи очков. Получить 7 очков можно лишь при следующих сочетаниях исходов броска двух костей: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих получению 7 очков, из 36 возможных исходов броска костей. Следовательно, вероятность будет равна 6/36 или, если сократить, 1/6. Для сравнения: вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше.

Определение вероятностного пространства

При построении математической модели мы должны найти компромисс между двумя обстоятельствами. С одной стороны, она должна быть достаточно подробной, чтобы учесть все существенные черты изучаемого явления. С другой стороны, необходимо отбросить все несущественные детали, затемняющие суть дела. Излишняя подробность затрудняет изучение свойств модели, а чрезмерное упрощение может привести к неправильным выводам относительно поведения реальной системы.

Мы начинаем изучение курса теории вероятностей с исследования свойств моделей таких случайных экспериментов, которые имеют конечное или счетное число исходов. Элементарным исходом мы будем называть такое событие, которое однозначно (с определенной точки зрения) говорит о том, чем закончился эксперимент. Это сразу же накладывает на множество элементарных исходов следующее важное ограничение: в каждом испытании происходит один и только один элементарный исход.

Чтобы понять, как должна выглядеть наша модель, рассмотрим пример. Однородный игральный кубик в одинаковых условиях подбрасывают много раз и отмечают число очков, выпавших на верхней грани. Ясно, что в этом эксперименте есть 6 элементарных исходов, которые мы обозначим ( означает, что выпало к очков). Пусть 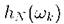- относительная частота появления исхода 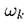. Тогда эти частоты обладают следующими свойствами:

1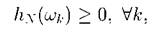

2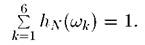

Как отмечалось выше, частоты тяготеют к некоторым числам, которые мы будем называть вероятностями этих исходов. Ясно, что они должны наследовать свойства частот. Эти предварительные рассмотрения приводят нас к следующему определению.

Определение 1. Дискретным вероятностным пространством называется пара 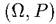, где 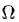-конечное или счетное множество, Р - вещественная функция, заданная на 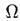, такая, что

1)

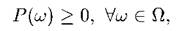
2)

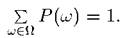
Множество 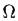называется пространством элементарных исходов, его элементы 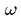-элементарными исходами, а число 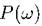- вероятностью появления элементарного исхода .

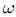Пример 1. Симметричную монету подбрасывают один раз. Здесь два элементарных исхода: выпал герб - Г, выпала цифра - Ц. Таким образом, 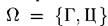. В силу симметрии естественно положить 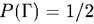5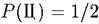

Пример 2. Однородный симметричный игральный кубик подбрасывают один раз. В этом случае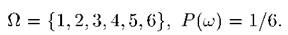

Другие примеры будут приведены на практических занятиях. Важную роль играет следующий частный случай дискретного вероятностного пространства.

Определение 2 . Говорят, что мы имеем задачу на классическое определение вероятности, если 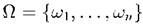-конечное множество и для всех 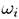, , 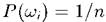т.е. все исходыравновозможны.

Обычно предположение о равновозможности исходов делается из соображений симметрии задачи. Но так ли это на самом деле (т.е. верна ли модель), можно установить только из сравнения с экспериментальными данными.

6. Геометрическая вероятность. Непрерывное вероятностное пространство. Пример.

Геометрическое определение

Несмотря на то, что классическое определение является интуитивно понятным и выведенным из практики, оно, как минимум, не может быть непосредственно применено в случае, если количество равновозможных исходов бесконечно. Ярким примером бесконечного числа возможных исходов является ограниченная геометрическая область G, например, на плоскости, с площадью S. Случайно «подброшенная» «точка» с равной вероятностью может оказаться в любой точке этой области. Задача заключается в определении вероятности попадания точки в некоторую подобласть g с площадью s. В таком случае, обобщая классическое определение, можно прийти к геометрическому определению вероятности попадания в подобласть g: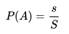

В виду равновозможности вероятность эта не зависит от формы области g, она зависит только от её площади. Данное определение естественно можно обобщить и на пространство любой размерности, где вместо площади использовать понятие «объёма». Более того, именно такое определение приводит к современному аксиоматическому определению вероятности. Понятие объёма обобщается до понятия меры некоторого абстрактного множества, к которой предъявляются требования, которыми обладает и «объём» в геометрической интерпретации — в первую очередь, это неотрицательность и аддитивность.

Непрерывное вероятностное пространство. Геометрические вероятности. Формула классической вероятности следующим образом обобщается на случай непрерывных множеств элементарных исходов .

Пусть – ограниченная замкнутая область на евклидовой плоскости, а условия опыта таковы, что вероятность попадания в произвольную подобласть области 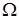пропорциональна площади этой подобласти и не зависит от ее местоположения в 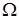. При этих условиях для вероятности наступления любого наблюдаемого в данном опыте события 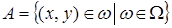справедлива формула геометрической вероятности:

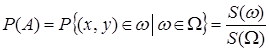, (2)

где 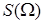– площадь области 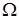, 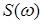– площадь подобласти .

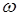Формула (2) естественным образом обобщается на случай пространств произвольной размерности:

,

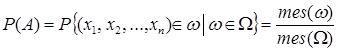где 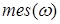– мера множества 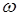(длина, площадь, объем и т. д. в зависимости от размерности того пространства, в котором рассматриваются данные множества).

Пример. На обслуживающее устройство в промежуток времени 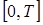должны поступить две заявки. Если разность между моментами поступления заявок меньше 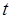, то вторая заявка теряется. Найти вероятность потери заявки.

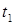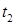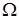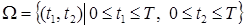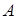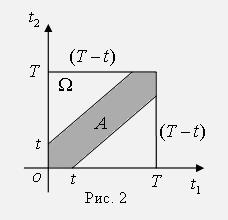
◄ Обозначим через и моменты поступления 1-й и 2-й заявок соответственно. Тогда множество можно записать в виде: . Искомое событие ={заявка будет потеряна} запишется в виде: 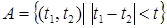. Если воспользоваться геометрически определением, то множества 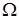и 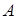изобразятся областями на плоскости, представленными на рис. 2. Площади этих фигур 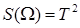, 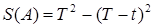. По формуле (2) находим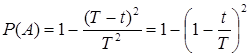

7. Теорема сложения вероятностей. Несовместные события.

Несовместные события — В теории вероятностей несколько событий называются несовместимыми, если никакие два из них не могут появиться одновременно в результате однократного испытания случайного эксперимента.

Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем .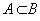

События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В.

Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

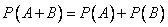
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:

.

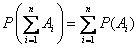Если случайные события 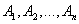образуют полную группу несовместных событий, то имеет место равенство

.

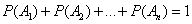Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле

.

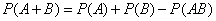События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей. Вероятность произведения независимых событий А и Ввычисляется по формуле:

.

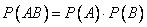Вероятность произведения зависимых событий вычисляется по формуле условной вероятности (см. следующий раздел).

Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим события: А – вынули белый шар из первого ящика,
;

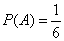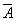- вынули черный шар из первого ящика,
;

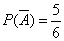В – белый шар из второго ящика,
;

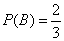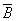- черный шар из второго ящика,
.

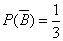Нам нужно, чтобы произошло одно из событи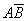й или 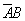. По теореме об умножении вероятностей
, .
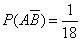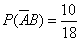Тогда искомая вероятность по теореме сложения будет
.

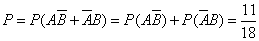Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.

Решение.

Пусть А – попадание первого стрелка, ;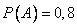

В – попадание второго стрелка, .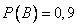

Тогда 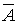- промах первого, ;

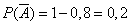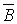- промах второго, .

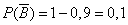Найдем нужные вероятности.

а) АВ – двойное попадание,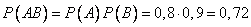

б) 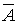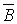– двойной промах, .

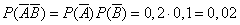в) А+В – хотя бы одно попадание,

.

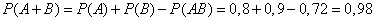г) 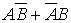– одно попадание,

.

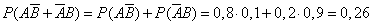Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

Решение.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

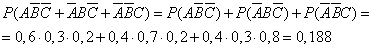
2. .

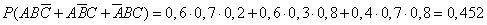3.

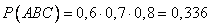
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий 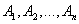, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

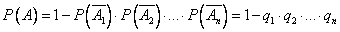
Если события 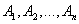имеют одинаковую вероятность 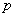, то формула принимает простой вид:

.

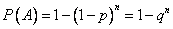Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события 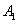(попадание первого орудия), 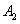(попадание второго орудия) и 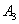(попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям 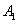, 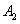и 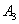(т. е. вероятности промахов), соответственно равны:

, ,

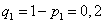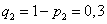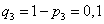
Искомая вероятность .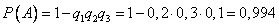

Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События "машина работает" и "машина не работает" (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: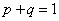

Отсюда вероятность того, что машина в данный момент не работает, равна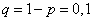

Искомая вероятность

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие "при n выстрелах стрелок попадает в цель хотя бы один раз". События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .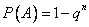

Приняв во внимание, что, по условию, 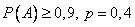(следовательно, 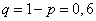), получим

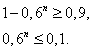
Прологарифмируем это неравенство по основанию 10:

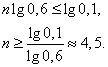
Итак, 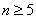, т.е. стрелок должен произвести не менее 5 выстрелов.

8. Условная вероятность. Теорема умножения вероятностей. Независимые события.

Условная вероятность

Наступление события 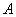может повлиять на вероятность появления события 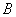. Для учета таких случаев вводится понятие условной вероятности события .

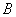Определение. Вероятность события 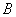, вычисленная при условии, что имело место событие 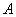, называется условной вероятностью события 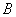и обозначается

.

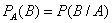Пример. Пусть событие 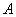- означает, что при бросании двух кубиков на первом выпала 1, а событие 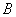- означает, что сумма очков, выпавших на двух костях больше 5. Найти вероятность .

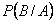Решение. Если на первомкубике выпала 1, то возможными исходами опыта являются исходы 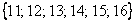. Событию 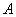при этом благоприятствуют исходы 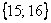, т.е. два из 6, значит,