Операции над случайными событиями. Диаграммы Венна.
(ФЭМ 1 курс, 2 семестр )
1. 
Понятие случайного эксперимента. Классификация событий, связанных со случайным экспериментом. Примеры.
Операции над случайными событиями. Диаграммы Венна.
В теории вероятностей случайными событиями являются подмножества множества элементарных исходов Ω .
Над событиями, как и над любыми множествами, можно совершать следующие операции.
Произведение (пересечение) двух событий
Операцию произведения (пересечения) двух событий A и B обозначают
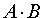, или AB , или 
.
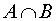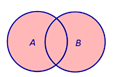
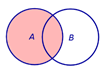
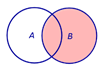
Определение 1. Произведением (пересечением) двух событий A и B называют такое событие, которое состоит из всех элементов, входящих как в событие A , так и в событие B (рис. 1).
| 
|
| Событие A | Событие B |
|
| |
| Событие | |
Рис.1
Сумма (объединение) двух событий
Операцию суммы (объединения) двух событий A и B обозначают
A + B или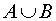 
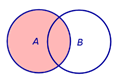
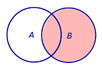
Определение 2. Суммой (объединением) двух событий A и B называют такое событие, которое состоит из элементов события A и элементов события B (рис. 2).
| 
|
| Событие A | Событие B |
|
| |
| Событие A + B | |
Рис.2
Разность двух событий
Операцию разности двух событий A и B обозначают
A \ B
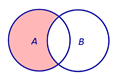
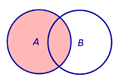
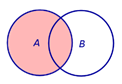
Определение 3. Разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B (рис. 3).
| 
|
| Событие A | Событие B |
|
| |
| Событие A \ B | |
Рис.3
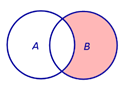
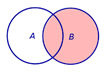
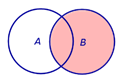
Замечание 1. Разностью событий B и A является событие B \ A , изображенное на рисунке 4.
| 
|
| Событие A | Событие B |
|
| |
| Событие B \ A | |
Рис.4
Симметрическая разность двух событий
Операцию симметрической разности двух событий A и B обозначают
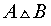
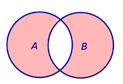
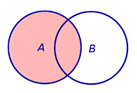
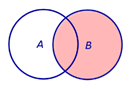
Определение 4 . Симметрической разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B , а также из тех элементов события B , которые не входят в событие A (рис. 5).
| 
|
| Событие A | Событие B |
|
| |
| Событие | |
Рис.5
Переход к противоположному событию
Событие, противоположное к событию A , обозначают
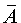или AC
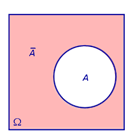
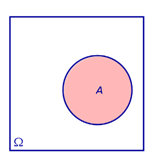
Определение 5. Противоположным событием к событию A называют событие, состоящее из тех элементов всего множества элементарных событий Ω , которые не входят в событие A (рис. 6).
| 
|
| Множество Ω | Событие A |
|
| |
| Событие | |
Рис.6
Замечание 2. Справедлива формула
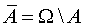
Определение 6. Событие Ω называют достоверным событием, пустое множество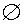 
называют невозможным событием.
Замечание 3. Рисунки, на которых наглядно показаны операции над множествами, называют диаграммами Эйлера-Венна. В частности, диаграммами Эйлера-Венна являются рисунки 1-6 .
3. Эмпирическое и аксиоматическое определения вероятности. Понятие вероятностного пространства.
Эмпирическое «определение» вероятности связано с частотой наступления события исходя из того, что при достаточно большом числе испытаний частота должна стремиться к объективной степени возможности этого события. В современном изложении теории вероятностей вероятность определяется аксиоматически, как частный случай абстрактной теории меры множества. Тем не менее, связующим звеном между абстрактной мерой и вероятностью, выражающей степень возможности наступления события, является именно частота его наблюдения.
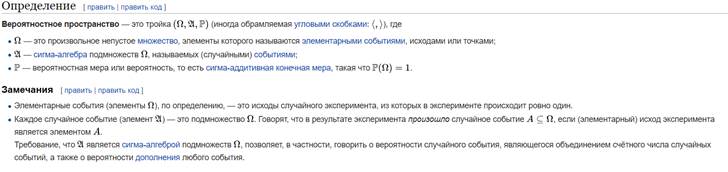Вероя́тностное простра́нство — понятие, введённое А. Н. Колмогоровым в 30-х годах XX века для формализации понятия вероятности, которое дало начало бурному развитию теории вероятностей как строгой математической дисциплины.
4. Свойства вероятности и следствия из них.
Существуют различные способы введения этой меры. Согласно аксиоматическому подходу, существование такой меры для каждого события постулируется, а свойства определяются совокупностью аксиом:
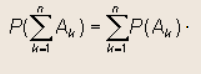Каждому событию А соответствует неотрицательное действительное число Р(А), называемое вероятностью события А.
Вероятность достоверного события равна единице, то есть .
Если А и В – несовместные события, то Р(А+В) = Р(А) + Р(В).
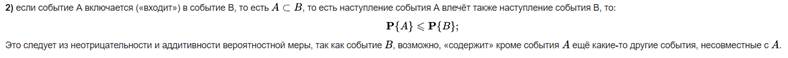
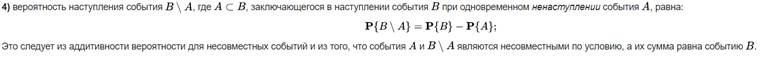
5. Классическая вероятность. Дискретное вероятностное пространство. Пример.