Тема урока: Соотношения между сторонами и углами прямоугольного треугольника.
18. 04. 2022 г. 8 класс.
Тема урока: Соотношения между сторонами и углами прямоугольного треугольника.
Цели урока:
Образовательная: – совершенствовать навыки решения задач на применение теории подобных треугольников.
Развивающая: – развивать умения устанавливать причинно-следственную связь; строить логические рассуждения, умозаключения и выводы; умение работать с геометрическим текстом.
Воспитательная: – формирование ответственного отношения к учению, формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, умения находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме.
Ход урока.
I. Организационный момент. Мотивация учебной деятельности.
II. Актуализация знаний учащихся.
Решить задачу № 576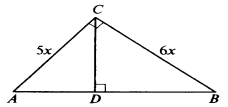 
Решение: Пусть Х — коэффициент пропорциональность, тогда АС = 5х, ВС = 6х.
Из ΔАСD (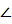 
D = 900) по теореме Пифагора АD2 = АС2 — СD2 = 25х2 — СD2.
Из ΔВСD ( 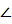D = 900) по теореме Пифагора ВD2 = СВ2 — СD2 = 36х2 — СD2
ВD2 — АD2 = (36х2 — СD2) — (25х2 — СD2) = 11х2
ВD2 — АD2 = (ВD — АD)(ВD + АD) = 11АВ, так как ВD на 11 см больше АD,
ВD + АD = АВ.
Следовательно 11х2 = 11АВ, отсюда АВ = х2
Из ΔАВС ( 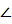С = 900) по теореме Пифагора АВ2 = АС2 + ВС2 = 25х2 + 36х2 = 61х2, отсюда АВ = х 
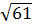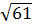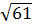; х2 = х ; х = ; АВ = 61 см.
Найти: СН, АС, ВС SАСН : SВСН.
Для решения задач на нахождение сторон и углов прямоугольного треугольника нужно вспомнить определения синуса, косинуса и тангенса.
Рассмотрим прямоугольный треугольник:
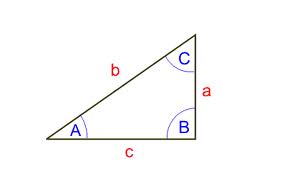Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Противолежащий катет - это тот катет, который лежит напротив угла, синус которого мы рассматриваем.
Например, для треугольника, который изображен на рисунке,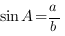 
, 
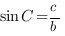
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Прилежащий катет - это тот катет, который является одной из сторон угла, косинус которого мы рассматриваем.
Например, для треугольника, который изображен на рисунке,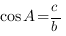 
, 
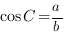
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Например, для треугольника, который изображен на рисунке,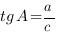 
, 
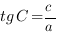
Задачи на нахождение сторон и углов прямоугольного треугольника решаются по такому алгоритму:
1. Выделяем треугольник, в который входит сторона или угол, который нам нужно найти.
2. Смотрим, какие элементы треугольника нам известны, и с помощью какой тригонометрической функции они между собой связаны.
3. Записываем соотношение, которое связывает между собой эти элементы,
Рассмотрим примеры решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике:
1. Задание В7 (№ 27217) В треугольнике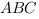 
угол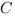 
равен 
, 
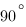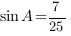. Найдите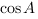 
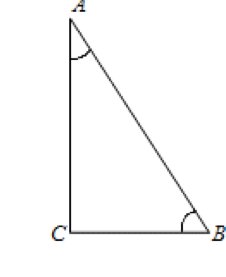
рис.1
Решим эту задачу двумя способами.
а. Так как требуется найти косинус угла, синус которого известен, мы можем воспользоваться основным тригонометрическим тождеством.
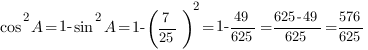
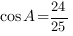
б.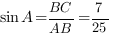 
Введем единичный отрезок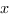 
, тогда 
, 
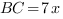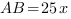
По теореме Пифагора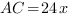 
.
Тогда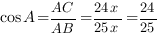 
Ответ: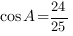
2. Задание В7 (№27220)
В треугольнике ABC угол C равен ,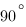 
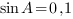. Найдите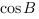 
Смотрим на рис.1:
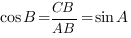
Значит,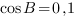 
Ответ: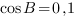
3. Задание В7 (№27221)
В треугольнике ABC угол C равен ,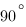 
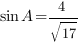. Найдите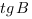 
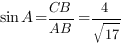
Введем единичный отрезок 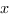, тогда 
, 
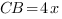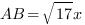
По теореме Пифагора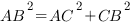 
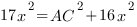
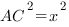
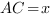
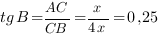
Ответ: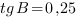 
4. Задание В7 (№27221)
В треугольнике ABC угол C равен , ,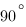 
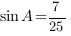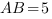. Найдите AC.
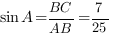
Введем единичный отрезок 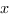, тогда ,
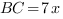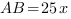
По теореме Пифагора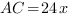
Найдем :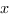 
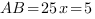- по условию.
Значит,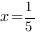 
. Отсюда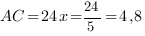 
Ответ: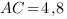 
5. Задание В7 (№27259)
В треугольнике ABC угол C равен ,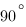 
, 
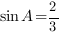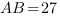. Найдите AH.
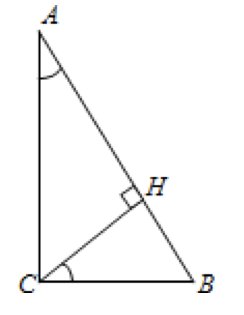
Найдем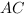 
из треугольника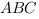
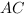- прилежвщий к углу 
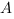катет, поэтому он связан с 
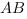через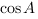
Найдем 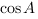с помощью основного тригонометрического тождества:
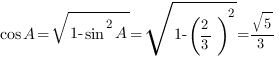
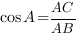, отсюда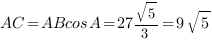 
Теперь рассмотрим треугольник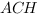 
, в котором 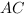- гипотенуза, а 
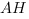- катет, связанные между собой через :
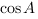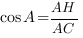, отсюда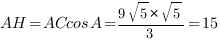 
Ответ: AH=15.