1 2.909e-03 6.000e+00 6.028e+00 7.318e+02 1.563e+05
Балтийский Госудраственный Технический Университет им. Д.Ф.Устинова « Военмех»
Лабораторная работа по курсу:
«Теория Механизмов и Динамика Машин»
на тему:
«структурный и кинематический анализ рычажного механизма»
вариант 3-15
выполнила: студентка 3 курса группы А-351
Калинина Анастасия
Проверил:
Воротынов Б.Н.
Санкт-Петербург.
2017.
1С труктурный анализ механизма:
На рисунке представлена схема исследуемого рычажного механизма, состоящего из трех звеьев, два из которых подвижны. Где 1 — кривошип, 2 — шатун, 3 — кулиса, 0,4 — неподвижные шарнирные опоры.
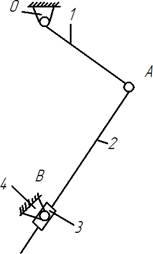 |
Табл.1
| 1 | 2 | 3 | 4 | |
| 1 | 1 | 1 | ||
| 2 | 1 | 1 | ||
| 3 | 1 | 1 | ||
| 4 | 1 | 1 |
Пассивных звеньев в механизме нет.
Число степеней свободы механизма по формуле Чебышева для плоских механизмов:
W =3n−2Pк−P в W=3*3-2*4=1.
Где n — число подвижных звеньев,
Pк — количество кинематических пар к-ого класса.
Структурное деленеие механизма:
Входное звено- кривошип : Структурные группы:
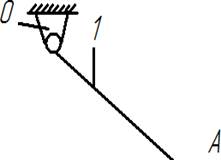 | 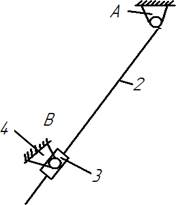 | ||
W=3*1-2*1=1 W=3*2-2*3=0
Обе структурные группы имеют 2-й класс, 2-й порядок, следовательно, и весь механизм является механизмом 2-го класса, 2-го порядка.
2. Кинематический анализ механизма:
Кинематический анализ механизма производится экспериментально-теоретически. Функцию положения F(φ) кулисы – 3 в зависимости от угла поворота кривошипа получаем экспериментально.
Будем считать.ю что кривошип вращается равномерно с ω1 = 10 с-1.
|
|
|
Полагая, что кривошип вращается равномерно, можем сказать что φ=ωt. Получаем функцию положения от времени F(t), её разлагаем в ряд Фурье и дифференциированием ряда определяем зависимости скорости V(t) и ускорения А(t) кулисы. При этом необходимо решить влопрос о достаточном числе членов ряда.
Разложение функции в ряд Фурье означает её приближенную замену тригонометрическим
F Ф (t) =
A0 +

|
2
å [A
|
|
|
j = 1
cos(w
t ) +
B sin(w
t )] =
полиномом вида:
= A0 +
 2
2
å C j j = 1
sin(w
j t + a j
Где T = 2π, t= 2π/60 = 0,105 c – время полного порота кривошипа.
|
|
С= А2B2 - амплитуда сигнала на j-той частоте
Частота сигнала для j-й гармоники θj = 2πjT.
Поскольку в данном случае функция F(t) задана таблицей значений в конечном числе точек m, то максимальное число членов ряда n=m/2=36/2=18.
Формулы для вычисления коэффициента ряда Фурье при табличном задании функции:
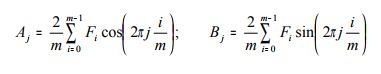
Где Fi - значения функции F(t) при t = 0,1,2,3,...m-t
В таблице ниже приведена экспериментальная зависимость функции перемещения кулисы F(φ) с шагом Δ φ — 10о по углу поворота кривошипа:
Таблица 2.1
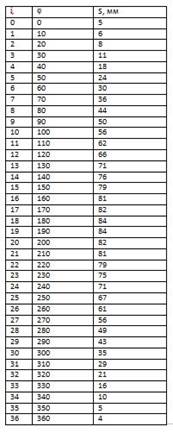
Шаг по времени при этом Δ t = Δ φ* ω = 10π/ (65*180) = 0,002909c.
Обработку данных эксперимента проведем с помощью программы ApproxFSP. На первом этапе разложим F(t) в ряд с максимально возможноым числом членов.
N=18. В этом случае значения ряда Фурье практически совпадают со данными эксперимента.
Таблица 2.2.
i t, c S, мм Ряд Произв-я 1 Произв-я 2
0 0.000e+00 5.000e+00 4.972e+00 7.582e+01 3.610e+04
1 2.909e-03 6.000e+00 6.028e+00 7.318e+02 1.563e+05
2 5.818e-03 8.000e+00 7.972e+00 5.157e+02 2.748e+04
3 8.727e-03 1.100e+01 1.103e+01 1.925e+03 6.406e+05
4 1.164e-02 1.800e+01 1.797e+01 2.362e+03 -2.603e+05
5 1.455e-02 2.400e+01 2.403e+01 1.999e+03 6.877e+04
6 1.745e-02 3.000e+01 2.997e+01 1.987e+03 -7.649e+04
7 2.036e-02 3.600e+01 3.603e+01 2.427e+03 3.645e+05
8 2.327e-02 4.400e+01 4.397e+01 2.648e+03 -3.529e+05
9 2.618e-02 5.000e+01 5.003e+01 1.727e+03 3.215e+04
10 2.909e-02 5.600e+01 5.597e+01 2.373e+03 6.136e+04
11 3.200e-02 6.200e+01 6.203e+01 1.566e+03 -3.599e+05
12 3.491e-02 6.600e+01 6.597e+01 1.456e+03 2.238e+05
13 3.782e-02 7.100e+01 7.103e+01 1.887e+03 -2.035e+04
14 4.073e-02 7.600e+01 7.597e+01 1.392e+03 -2.632e+05
15 4.364e-02 7.900e+01 7.903e+01 7.961e+02 -1.019e+05
16 4.654e-02 8.100e+01 8.097e+01 5.042e+02 -1.538e+05
17 4.945e-02 8.200e+01 8.203e+01 4.038e+02 1.871e+05
18 5.236e-02 8.400e+01 8.397e+01 7.040e+02 -2.576e+05
19 5.527e-02 8.400e+01 8.403e+01 -7.040e+02 -3.220e+05
20 5.818e-02 8.200e+01 8.197e+01 -4.076e+02 2.459e+05
21 6.109e-02 8.100e+01 8.103e+01 -4.786e+02 -1.890e+05
22 6.400e-02 7.900e+01 7.897e+01 -9.393e+02 -2.260e+05
23 6.691e-02 7.500e+01 7.503e+01 -1.689e+03 -3.300e+04
24 6.982e-02 7.100e+01 7.097e+01 -1.002e+03 1.158e+05
25 7.272e-02 6.700e+01 6.703e+01 -2.020e+03 -4.279e+05
26 7.563e-02 6.100e+01 6.097e+01 -1.701e+03 3.507e+05
27 7.854e-02 5.600e+01 5.603e+01 -2.179e+03 -4.859e+05
28 8.145e-02 4.900e+01 4.897e+01 -2.172e+03 3.801e+05
29 8.436e-02 4.300e+01 4.303e+01 -2.438e+03 -5.213e+05
30 8.727e-02 3.500e+01 3.497e+01 -2.493e+03 5.415e+05
31 9.018e-02 2.900e+01 2.903e+01 -2.217e+03 -5.498e+05
32 9.309e-02 2.100e+01 2.097e+01 -2.655e+03 6.400e+05
33 9.600e-02 1.600e+01 1.603e+01 -1.272e+03 -3.064e+05
34 9.891e-02 1.000e+01 9.972e+00 -2.648e+03 1.338e+05
35 1.018e-01 5.000e+00 5.028e+00 -4.647e+02 7.015e+05
Результаты дифференциирования рядов по времени представлены выше, а графики скорости и ускорений ниже:
Рис. 2.1
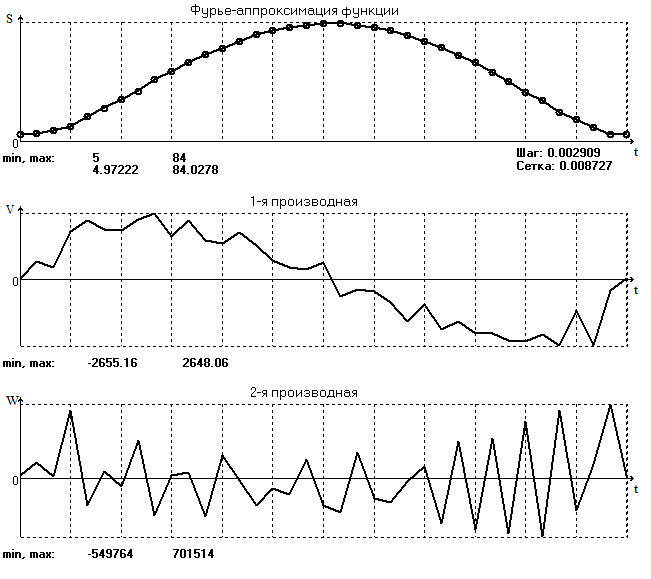
На графике скорости и особенно ускорения видны поразитные осциляции, вызванные погрешностями замера занчений F(t), появляется необходимость сглаживания этих зависимостей.
Оценим значимость членов ряда с помощью амплитудного спектра , показанного на рисунке 2.2 и табл. 2.3
Рис. 2.2.
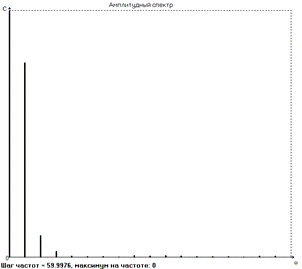
Табл. 2.3
i Част.,1/c Част., гц Ci Фазы i
0 0.000e+00 0.000e+00 4.869e+01
1 6.000e+01 9.549e+00 3.838e+01 1.4966
2 1.200e+02 1.910e+01 4.288e+00 1.5127
3 1.800e+02 2.865e+01 1.106e+00 -1.5273
4 2.400e+02 3.820e+01 2.687e-01 -1.4345
5 3.000e+02 4.774e+01 1.076e-01 -0.5944
6 3.600e+02 5.729e+01 1.470e-01 -1.2373
7 4.200e+02 6.684e+01 6.947e-02 -1.3046
8 4.800e+02 7.639e+01 3.421e-01 0.5496
9 5.400e+02 8.594e+01 2.003e-01 -0.5880
10 6.000e+02 9.549e+01 3.639e-01 0.4369
11 6.600e+02 1.050e+02 2.649e-01 -1.0935
12 7.200e+02 1.146e+02 1.470e-01 -0.1901
13 7.800e+02 1.241e+02 1.601e-01 -1.1959
14 8.400e+02 1.337e+02 1.524e-01 0.2919
15 9.000e+02 1.432e+02 6.908e-02 -0.8003
16 9.600e+02 1.528e+02 2.465e-01 -0.7654
17 1.020e+03 1.623e+02 2.485e-01 -0.0946
18 1.080e+03 1.719e+02 5.556e-02 -1.5708
Анализ амплитудного спектра исследуемой функции показывает, что основными частотами, присутствующими в сигнале (кроме Aо/2), являются лишь первые две: p1 = 60 рад/с и р2=120рад/с.
Предположим, что именно эти частоты несут информацию лишь о перемещении ползуна, а на остальных частотах содержится лишь информацию о «шуме» и проведём разложение в ряд и аппроксимацию функции с учетом только этих двух частот. Результаты представлены на рис. 2.2
и табл. 2.4, иллюстрирующие эффект сглаживания.
Рис.2.3
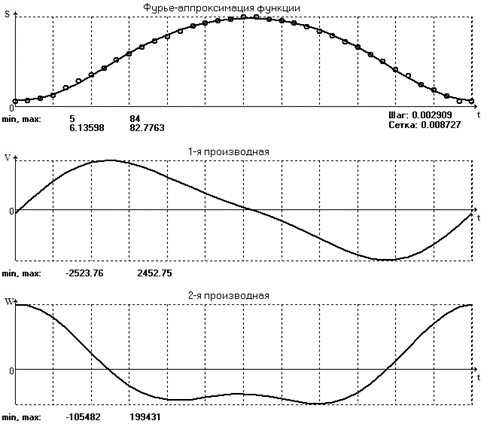
Табл. 2.4
i t, c S, мм Ряд Произв-я 1 Произв-я 2
0 0.000e+00 5.000e+00 6.136e+00 -2.007e+02 1.994e+05








