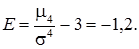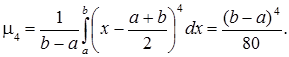Обчислення ймовірності заданого відхилення. Правило “трьох сигм”.
Нехай відомі параметри m і s нормально розподіленої випадкової величини Х. Знайдемо ймовірність того, що випадкова величина Х відхиляється від центра розсіяння m на величину, меншу за s:
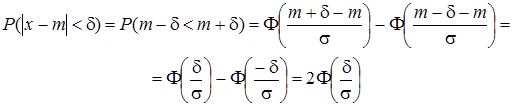(1)
Перетворимо формулу (1), поклавши d = st Þ Р(|X – m|<st) = 2F(t)
t = 1: P(|X-m|<s) = 2F(1) = 0,6827;
t = 2: P(|X-m|<2s) = 2F(2) = 0,9545;
t = 3: P(|X-m|<3s) = 2F(3) = 0,9973.
Звідси видно, що “практично вірогідним” є виконання нерівності |x – m| < 3s, тобто лише у 0,27 % випадків абсолютна величина перевищить потроєне середнє квадратичне відхилення.
У цьому складається “правило трьох сигм”. Інакше: майже вірогідним є той факт, що випадкова величина (наприклад, похибка виміру), розподілена за нормальним законом, не відхилиться від математичного сподівання по модулю більше ніж на 3s.
На практиці правило “трьох сигм” застосовується так: якщо розподіл випадкової величини невідомий, але умова правила “трьох сигм” виконана, то маємо підставу стверджувати, що випадкова величина розподілена нормально.
2.6. Поняття про теорему Ляпунова
Нормально розподілена випадкова величина широко розповсюджена на практиці. Чим це пояснюється? Відповідь нам дав видатний російський математик О.М. Ляпунов в його центральній граничній теоремі. Приводимо наслідок із цієї теореми.
Якщо випадкова величина Х уявляє собою суму великої кількості взаємно незалежних випадкових величин, вплив кожної з яких на всю суму дуже мале, то Х має розподіл, близький до нормального.
На практиці найбільш часто зустрічаються саме такі випадкові величини.
Наприклад, вимірюється деяка фізична величина. Любий вимір дає лише наближене значення цієї величини, так як на результати вимірів впливають дуже багато незалежних випадкових факторів (температура середовища, коливання приладу, вологість повітря, кваліфікація експериментатора і т.п.)
Кожний з цих факторів породжує незначну “частинну похибку”. Але завдяки тому, що число цих факторів дуже велике, сумарна їх дія породжує вже значну похибку (“точну похибку”). Цю сумарну похибку ми вважаємо випадковою величиною, розподіленою за нормальним законом.
2.7. Показниковий розподіл
В теорії масового обслуговування, дослідженні операцій, фізиці, питаннях надійності та ін. Часто зустрічаються величини, розподілені за показниковим законом.
Неперервна випадкова величина Х має показниковий, або експоненціальний, розподіл з параметром l > 0, якщо її щільність ймовірності має вигляд :
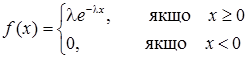
Функцію розподілу випадкової величини Х знайдемо за формулою
 |
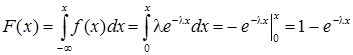
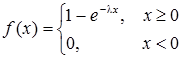
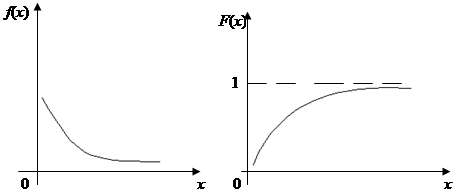Числові характеристики:
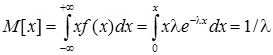
(інтеграл брали частинами: u = x, dv = dx, du = dx, v =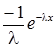 
).
Тобто математичне сподівання випадкової величини Х, розподіленої за показниковим законом, обернений коефіцієнту l.
Для визначення дисперсії, двічі інтегруючи частинами, знайдемо значення другого початкового моменту для випадкової величини Х, розподіленої за показниковим законом
a2[x] = l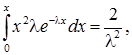 
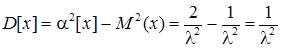
Середньоквадратичне відхилення s[x]=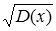 
.
Коефіцієнти варіації v =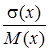 
= 1.
Значення медіани знаходимо із співвідношення F(x0) = 1/2:
.
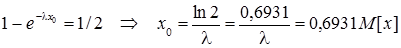Коефіцієнти асиметрії
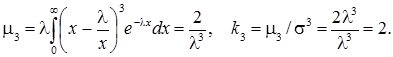
Приклад. Випадкова величина Т – час роботи радіолампи має показниковий розподіл. Визначити ймовірність того, що час роботи радіолампи буде не менше 600 годин, якщо середній час роботи радіолампи 400 годин.
M[x] = 400; l = 1/M[x] = 1/400.
P(T ³ 600) = 1 – P(T < 600) = 1 – F(600) =
= 
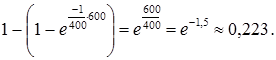
2.8. Рівномірний розподіл
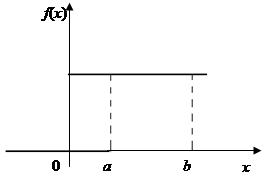
Неперервна випадкова величина має рівномірний розподіл на інтервалі (а, b), якщо всі її можливі значення неперервно заповнюють цей інтервал і рівноймовірні на ньому, тобто
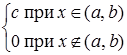
Рівномірний розподіл називають також законом рівномірної щільності. При визначенні рівномірного розподілу можна говорити про рівномірний розподіл випадкової величини Х на інтервалі або відрізку, оскільки ймовірність попадання в точку дорівнює нулю.
Виходячи з умови нормування щільності розподілу, знайдемо значення С:
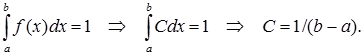
Отже
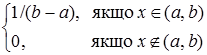
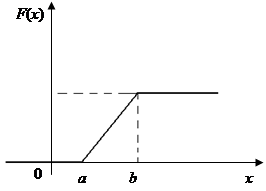
Функція розподілу
F(x) =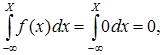 
якщо x £ a
F(x) =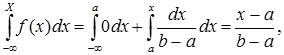 
якщо x Î (a, b]
F(x) =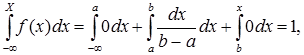 
якщо x >b .
Таким чином,
 |  | ||
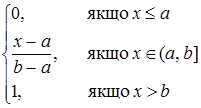
P(a < x < b) = F(b) – F(a) =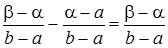 
.
Математичне сподівання M[x] =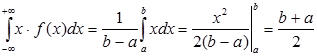 
.
Дисперсія D[x] =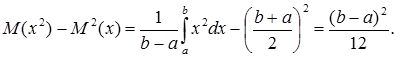 
Середньо квадратичне відхилення s[x] =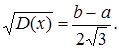 
З графіка щільності ймовірності рівномірно розподіленої випадкової величини Х випливає, що моди немає, а медіана
Me =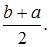 
Ексцес неперервно розподіленої випадкової величини Х має таке значення:
