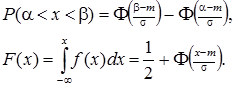Розв’язання: вказані ймовірності набувають значень
Р(X = 1) = 0,6; Р(X = 2) = 0,4×0,5 = 0,2;
Р(X = 3) = 0,4×0,5×0,6 + 0,4×0,5×0,4 = 0,2.
Знайдемо ряд розподілу
| Х | 1 | 2 | 3 |
| Р | 0,6 | 0,2 | 0,2 |
M[х] = 1×0,6 + 2×0,2 + 3×0,2 = 1,6
2.4.1.2. Мода дискретної випадкової величини. Медіана
Модою дискретної випадкової величини називається найімовірніше її значення. Вона позначається через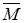 
.
Для ряду
| х | 1 | 2 | 3 | 4 |
| р | 0,1 | 0,4 | 0,3 | 0,2 |
мода 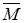= 2.
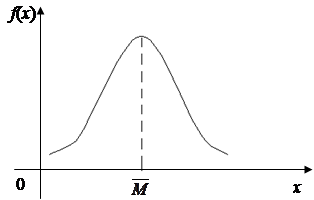Для неперервної випадкової величини модою являється те значення Х, в якому щільність ймовірності максимальна.
У загальному випадку математичне сподівання і мода випадкової величини не співпадають.
Часто застосовується ще одна характеристика положення – так звана медіана випадкової величини. Цією характеристикою, як правило, користуються тільки для неперервних випадкових величин, хоча формально її можна визначити і для дискретної випадкової величини.
Медіаною випадкової величини Х називається таке її значення M е, для якого Р(Х < M е) = P(X > M е), тобто однаково ймовірно, чи буде випадкова величина Х менша за M е, чи більша за M е.
Оскільки площа, розташована між віссю абсцис і кривою щільності ймовірності, дорівнює одиниці, то рівність можна записати у вигляді
P(X < M е) = P(X > M е) = 1/2.
Очевидно, якщо крива щільності ймовірності симетрична відносно математичного сподівання, то значення характеристики положення – математичне сподівання, моди і медіани – збігаються.
2.4.2. Моменти випадкових величин
У теорії ймовірностей і математиці широко використовуються числові характеристики, що називаються моментами. Найбільш поширені початкові та центральні моменти.
Для ряду розподілу дискретної випадкової величини
| Х | х1 | х2 | ... | хn |
| Р | р1 | р2 | ... | pn |
початковим моментом ai дискретної випадкової величини Х і-ого порядку називається математичне сподівання і-ого степеня цієї випадкової величини:
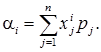
Аналогічно визначається початковий момент і-ого порядку для неперервної випадкової величини, якщо ¦(х) – щільність ймовірності:
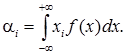
Якщо M[x] – математичне сподівання для випадкової величини Х, то центрованою випадковою величиною називається відхилення випадкової величини від математичного сподівання:
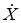= X – M[x].
Центральним моментом mi і-ого порядку дискретної випадкової величини Х називається математичне сподівання і-ого степеня центрованої випадкової величини:
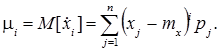
Для неперервної випадково величини Х і-ий центральний момент визначається формулою
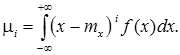
Особливе положення серед центральних моментів належить другому центральному моменту (і = 2), який позначають через D[x] або Dx і називають дисперсією випадкової величини. Для дискретних випадкових величин
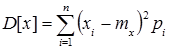
для неперервних випадкових величин
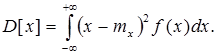
Іншими словами: дисперсія – математичне сподівання квадрата центрованої випадкової величини
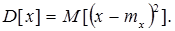
Дисперсія характеризує розкид випадкової величини відносно математичного сподівання і має розмірність квадрата випадкової величини.
На практиці часто користуються поняттям середньоквадратичного відхилення як квадратного кореня з дисперсії:
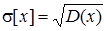
s[x] має розмірність випадкової величини. У практичних розрахунках використовується коефіцієнт варіації
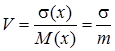
Ця величина характеризує ступінь випадковості. Наприклад, його обчислили для двох рядів дискретних випадкових величин. Той із рядів, що має більший коефіцієнт варіації, має і більший розкид випадкової величини.
Для характеристики симетрії розподілу випадкових величин відносно математичного сподівання використовують коефіцієнт асиметрії:
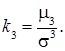
Якщо розподіл симетричний відносно математичного сподівання, то k3 = 0.Чим більша асиметрія розподілу випадкових величин відносно математичного сподівання, тим більше за модулем значення коефіцієнта асиметрії. Для характеристики крутості кривої щільності ймовірності неперервної випадкової величини використовують ексцес:
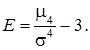
Для нормального закону розподілу Е = 0.Якщо Е > 0, вершина кривої щільності ймовірності розміщена вище кривої щільності ймовірності нормального закону, і навпаки, якщо Е < 0, то вершина кривої щільності ймовірності розміщена нижче кривої щільності ймовірності нормального закону розподілу.
2.4.3. Основні властивості числових характеристик
1. Математичне сподівання центрованої випадкової величини:
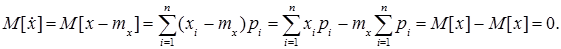
Отже математичне сподівання центрованої випадкової величини дорівнює нулеві. Доведення для неперервної випадкової величини аналогічне.
2. Дисперсія випадкових величин
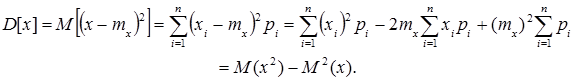
Тобто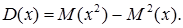 
Дисперсія випадкової величини дорівнює другому початковому моменту без квадрата математичного сподівання.
3. Аналогічно можна довести, що третій центральний момент
m3 = a2– 3a2mx + 2(mx)2.
4. Математичне сподівання константи
M[C] = C ×1 = C.
Математичне сподівання константи дорівнює самій константі.
5. Математичне сподівання суми випадкової і невипадкової величини дорівнює сумі математичних сподівань цих величин.
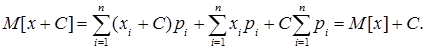
6. Константу можна виносити за знак математичного сподівання.
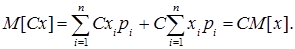
7. Дисперсія сталої величини дорівнює нулю.
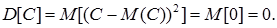
8. Дисперсія центрованої і нецентрованої випадкової величини дорівнюють одна одній.
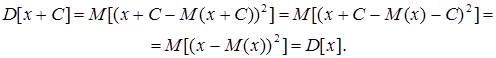
9. Постійний множник виноситься у квадраті за знак дисперсії.
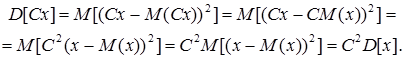
2.5. Закони розподілу випадкових величин
2.5.1. Нормальний закон розподілу ймовірності неперервної випадкової величини
Нормальний розподіл в теорії ймовірності займає особливе місце, є найбільш розповсюдженим. Нормальному закону підкоряються ті величини, значення яких визначаються багатьма незалежними причинами, причому кожна з них впливає на випадкову величину незначно. Наприклад, випадкова величина – похибка виміру – може бути представлена як сума великої кількості порівняно малих доданків – елементарних похибок, кожна з яких викликана дією окремих причин, що залежить від інших. Яким би законам розподілу не була підлегла окрема елементарна похибка, особливості їх у сумі великого числа доданків, і сума опиняється підкореною до закону, близького до нормального.
 |
Нормальний закон розподілу характеризуються щільністю ймовірності виду:
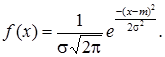
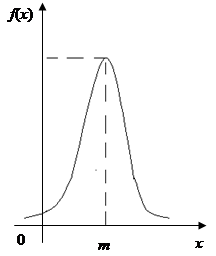
Крива розподілу по нормальному закону (крива Гауса) має холмоподібний вигляд, симетрична відносно прямої х = m.
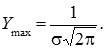
Щільність розподілу ¦(х) ® 0 при х ® ±¥.Ми бачимо, що нормальний розподіл визначається двома параметрами : m і s.
З’ясуємо їх зміст, для чого знайдемо основні числові характеристики випадкової величини Х – математичне сподівання і дисперсію.
а) за означенням математичне сподівання неперервної випадкової величини
( 
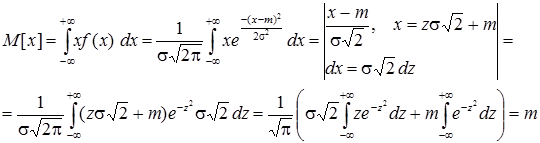
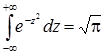– інтеграл Ейлера-Пуассона).
Таким чином, M[x] = m, тобто параметр дорівнює математичному сподіванню.
б) за визначенням дисперсії неперервної випадкової величини і враховуючи, що M[x] = mx = m, маємо
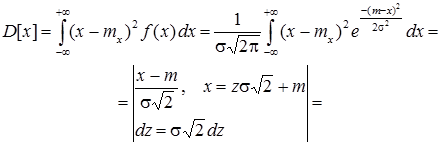
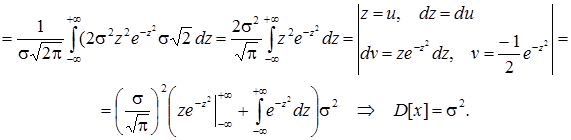
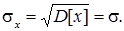
Тобто параметр s дорівнює середньому квадратичному відхиленню.
З’ясуємо, як впливають параметри m і s на форму кривої Гауса.
 |
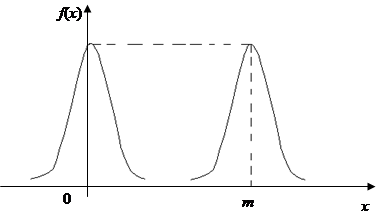Відомо, що графік функції ¦(х – m) одержується з графіка функції ¦(х) шляхом зсуву останнього на величину х = m при s = соnst; графік ¦(х) зміщується вздовж вісі ОХ, не змінюючи своєї форми f(x)
Із зростанням s максимальна ордината нормальної кривої спадає, а сама крива стає більш пологою, тобто стискується до вісі ОХ; при спаданні s нормальна крива стає більш “гостровершинною” і розтягується у додатному напрямі вісі О Y.
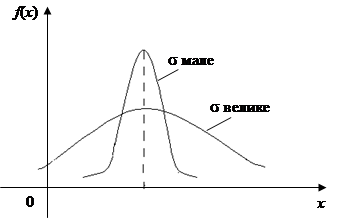
Якщо у формулі щільності ймовірностей покласти s = 1 і m = 0, то дістанемо нормовану щільність закону розподілу:
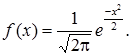
Інтеграл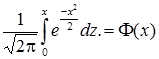 
=F(х) називають інтегралом ймовірностей або функцією Лапласа. Він не береться в елементарних функціях і для нього існують спеціальні таблиці. F(–х) = –F(х); при х ³ 5 F(х) = 1/2. Ex = 0; k3 = 0.
2.5.2. Ймовірність набування значення із заданого інтервалу випадкової величини Х, розподіленої за нормальним законом
Як відомо, якщо випадкова величина Х задана щільністю розподілу ¦(х), то ймовірність того, що Х приймає значення з інтервалу (a, b) таке:
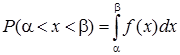. У нашому випадку
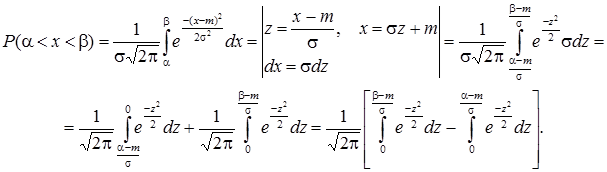
Застосовуючи до останньої різниці функцію Лапласа, остаточно дістанемо:
