Частина 2. Випадкові величини

Дата: 2025-05-25; Просмотры: 4
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

2.1. Види випадкових величин. Ряд розподілу.

Многокутник розподілу

Подальшим узагальненням і розширенням поняття випадкової події є випадкова величина.

 

Означення. Випадковою називається величина, яка у результаті випробування може прийняти те, чи інше значення, заздалегідь невідоме.

Випадкову подію можна розглядати як випадкову величину, що приймає тільки два значення – одиницю, коли подія відбулася (вірогідна) і нулю, коли – не відбулася (неможлива).

Усі результати, одержані раніше для випадкових подій, можна використати для випадкових величин. На практиці зустрічаються із двома видами випадкових величин: дискретними і неперервними.

Випадкова величина називається дискретною, якщо вона набуває окремих значень, які можна перерахувати (перенумерувати).

Приклади.

а) при киданні грального кубика число очок, що з’являється (1, 2, ..., 6);

б) число кораблів, що обробляються у порту за певний час;

в) число хлопчиків, що народжуються на кожну сотню пологів.

Неперервною випадковою величиною називається величина, можливі значення якої неперервно заповнюють деякий проміжок, і їх не можна перерахувати.

Приклади.

а) амплітуда морської хвилі у даній точці у даний момент часу;

б) швидкість повітря;

в) час очікування телефонного дзвінка.

У подальшому будемо випадкові величини позначати великими літерами X, Y, Z, ..., а їх можливі значення – маленькими літерами x, y, z, ... .

Для завдання дискретної випадкової величини треба перерахувати всі числові значення, які вона може прийняти і вказати їх ймовірності.

Задамо дискретну випадкову величину Х таблицею:

х х1 х2 ... хn
р р1 р2 ... рn

Одержана таблиця називається рядом розподілу дискретної випадкової величини Х.

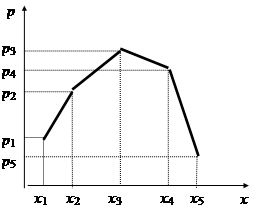Для того, щоб надати ряду розподілу більш наочний вигляд, застосовують його графічне зображення: по осі абсцис відкладають всі можливі значення випадкових величин, а по осі ординат – ймовірності цих значень. Фігура, утворена послідовним з’єднанням здобутих точок відрізками прямих, називається многокутником розподілу. І ряд розподілу, і многокутник розподілу повністю характеризують закон розподілу дискретної випадкової величини.

Оскільки х1, х2, ..., хn – всі можливі значення Х і утворюють повну групу несумісних подій, то

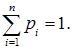
Введемо позначення: Р(Х = хі) = рі – ймовірність того, що випадкова величина Х приймає значення хі, дорівнює рі.

Приклад. Відбувається пальба по мішені. Ймовірність кожного влучення – р. Пальба відбувається до першого попадання. Випадкова величина Х – число зроблених пострілів. Побудувати ряд розподілу.

Розв’язання: можливі значення величини Х: 1, 2, 3,...Для того, щоб величина Х прийняла значення 1, необхідно, щоб подія А (влучення у ціль) відбулося при першому пострілі і його ймовірність р. Для того, щоб величина Х прийняла значення 2, необхідно, щоб при першому пострілі подія А не відбулася, а при другому – відбулася; ймовірність цього дорівнює pq (q = 1 – p).

Ряд розподілу:

Х 1 2 3 ... n
p p p q pq² ... pqⁿ‾¹

 

Для контролю підрахуємо суму ймовірностей:

 

 

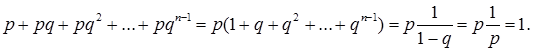
2.2. Функція розподілу

 

Всі можливі значення неперервної випадкової величини на відміну від дискретної не можна перерахувати, отже, неможливо задати закон розподілу для неперервної випадкової величини за допомогою ряду розподілу або многокутника розподілу.

Універсальною порівняно з рядом розподілу і многокутником розподілу є функція розподілу. Для функції розподілу використовуємо не ймовірність події Х = х, а ймовірність події Х < х.

 

 

Означення. Функцією розподілу (інтегральною функцією) F(х) називається ймовірність події, яка полягає в тому, що випадкова величина Х набуває значення меньше деякої змінної х: F(x) = P(X < x).

F(x) годиться як для дискретних, так і для неперервних випадкових величин.

Сформулюємо деякі загальні властивості функції розподілу (без доведення).

1. 0 £ F(x) £ 1 – ця властивість випливає із означення функції розподілу як ймовірності.

2. F(x) – неспадаюча функція свого аргументу, тобто при х2 > х1 F(x2) ³ F(x1) : F(х1) = Р(Х < x1), F(x2) = P(X < x2).

Рівність можлива тоді, коли немає шансів попасти в інтервал (х1, х2).

 

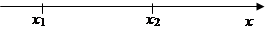
3. F(–¥) = 0.

4. F(+¥) = 1.

 

Ці рівності легко пояснити виходячи із геометричного змісту функції розподілу – ймовірність того, що випадкова величина набуває значень, розташованих зліва від точки х.

 


 

Якщо будемо необмежено переміщувати точку х вліво по осі абсцис, то попадання випадкової величини Х лівіше х у границі стає неможливою подією; природньо покласти, що ймовірність цієї події прямує до нуля, тобто F(–¥) = 0. Аналогічним чином необмежено переміщуючи точку х вправо, переконаємось, що F(+¥) = 1.

 

Графік функції F(х) є графік неспадаючої функції:

 

 

 

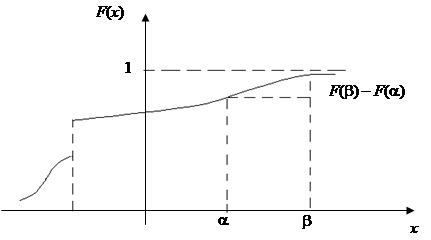Знайдемо ймовірність того, що випадкова величина Х попадає на ділянку від a до b.Умовимося лівий кінець ділянки включати, а правий не включати, тобто a £ Х < b.Виразимо ймовірність цієї події через функцію розподілу величини Х.Для цього розглянемо три події: подія А полягає в тому, що Х < b, подія В – Х < a, подія С – a £ Х < b.

Враховуючи, що А = В + С, згідно з теоремою додавання ймовірностей несумісних подій маємо:

Р(Х < b) = P(X < a) + P(a £ X < b) або F(b)=F(a)+P(a£X<b) Þ

P(a £ X < b) = F(b) – F(a), (1)

тобто ймовірність попадання випадкової величини на заданий проміжок дорівнює приросту функції розподілу на цьому проміжку.

Чим більше крутість ділянки, тим більша ймовірність попасти на проміжок (a, b).

 


Нехай функція розподілу F(x) неперервна. Знайдемо

Р(x £ X < x + Dx) = F(x + Dx) – F(x) = DF(x).

Знайдемо границю ймовірності при Dх ® 0 :

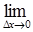P(x £ X < x + Dx)= 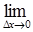DF(x) (2)

Оскільки функція розподілу неперервна, нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції. Звідси випливає, що 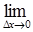DF(x) = 0.

Звідси: для неперервної випадкової величини ймовірність набування конкретного значення внаслідок досліду практично дорівнює нулю. Тоді

P(a £ X < b) = P(X = a) + P(a < X < b) =F(b) – F(a) (3)

 

Здобутий результат можна порівняти з масою точки. Густина речовини відмінна від нуля, а маса точки цієї речовини практично дорівнює нулю.

 

2.3. Щільність розподілу

 

Нехай для неперервної випадкової величини Х відома функція розподілу F(х), яку вважаємо диференційованою.

Відомо, що P(x < X < X + DX) = DF(X).

Визначимо середнє значення ймовірності на цьому проміжку, поділивши знайдену ймовірність на Dх:

.

 

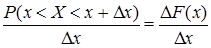Шукаємо границю цього відношення при Dх ® 0.Згідно з означенням границі відношення приросту функції до приросту аргументу маємо

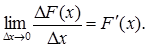
Позначимо F’(х) = ¦(х) (*) і назвемо щільністю розподілу (щільністю ймовірності, диференціальною функцією).


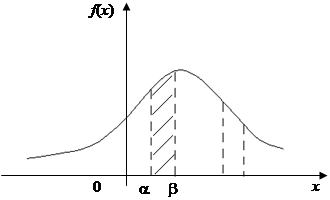
F(x) являється вичерпною характеристикою випадкових величин, але по ній важко судити про характер розподілу випадкових величин у нескінченно малому околі точки числової вісі. А тому і вводиться ще й щільність розподілу ¦(х).Крива у = ¦(х) називається кривою розподілу випадкової величини X.

 

Із означення щільності розподілу випливає, що вона не може бути від’ємною, як похідна від незростаючої функції.

Виразимо функцію розподілу F(x) через щільність розподілу ¦(х).Знайдемо інтеграл від (*) в межах від –¥ до х:

 

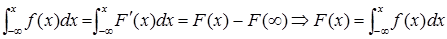(2)

 

Виразимо через щільність розподілу ймовірність попадання випадкової величини Х у заданий інтервал (a, b) :

 

Р(a < X < b) = F(b) – F(a) = 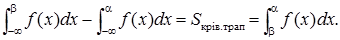(3)

 

Геометрично ймовірність попадання випадкової величини Х в інтервал (a, b) являє собою площу фігури, яка обмежена знизу віссю абсцис, зверху кривою щільності розподілу, а з боків ординатами х = a і х = b.

Ймовірність того, що випадкова величина Х попадає між точками x і х + dx:

площа прямокутника

P(x < X < x + dx) » ¦(x)dx – елемент ймовірності

 

 

Покладаючи a = –¥, b = +¥, одержуємо P(–¥ < X < +¥) = = 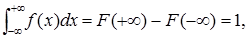тобто площа, розташована під кривою розподілу дорівнює одиниці.

Закон розподілу випадкових величин через щільність розподілу більш зручний, ніж функція розподілу, але використовується лише для неперервних випадкових величин.

 

2.4. Числові характеристики випадкових величин

Числові характеристики випадкових величин відіграють важливу роль у теорії ймовірностей і статистиці. У практиці дослідження випадкових величин іноді бувають невідомими закон їх розподілу або його параметри, може статися, що закон розподілу відомий, проте він не дає повного уявлення про випадкову величину. Тоді слід користуватися числами, які описують випадкові величини сумарно. Такі числа, які описують сумарно найістотніші характеристики розподілу, називаються числовими характеристиками випадкових величин.

 

2.4.1. Числові характеристики положення

 

До цих характеристик належать: математичне сподівання, мода і медіана.

 

2.4.1.1. Математичне сподівання

 

Розглянемо математичне сподівання дискретної випадково величини. Нехай задано ряд розподілу

 

x x1 x2 x3 ... xn
p p1 p2 p3 ... pn

 

Нехай відбулося N незалежних дослідів, в кожному із яких величина Х прийняла певне значення. Припустимо, що

х1 з’явилося m1 разів,

х2 з’явилося m2 разів,

……………………..

хі з’явилося mі разів.

Безперечно, що .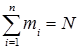

Обчислимо середнє арифметичне спостережених значень випадкових величин Х, яке позначимо через 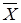або M*[X]:

 

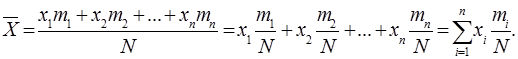
Але 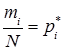– відносна частота і тоді

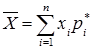(1)

Як довів Бернуллі при зростанні числа дослідів N відносна частота 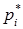наближається (сходиться за ймовірністю) до відповідної рі. Отже і середнє арифметичне 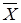(M*[x]) наближається до 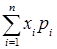.Остання величина позначається через M[x] або mx і називається математичним сподіванням випадкової величини:

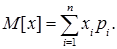(2)

Із порівняння (1) і (2) видно, що середнє арифметичне спостережених значень випадкових величин при великому числі дослідів як завгодно близько підходить до математичного сподівання.

Для неперервної випадкової величини Х математичне сподівання, природньо, виражається все не сумою, а інтегралом

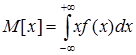(3)

де ¦(х) – щільність розподілу випадкової величини Х.

Формула (3) одержується із (2), якщо в неї замінити окремі значення хі неперервно змінюючимся параметром х, ймовірності рі – елементом ймовірності ¦(х)dx, кінцеву суму інтегралом.

Приклад. Ймовірність придбання потрібної речі у першій крамниці дорівнює 0,6, у другій – 0,5, у третій – 0,4.Скласти ряд розподілу числа відвідуваних крамниць, якщо покупець відвідує наступну крамницю за умови, що потрібної речі не виявилося у попередній. Знайти математичне сподівання.