10. Реальные газы. Водяной пар как пример реального газа.
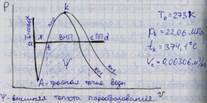
1. Запишите и рассмотрите уравнение состояния Ван-дер-Ваальса. Покажите в p - V координатах изотермы Ван-дер-Ваальса для температуры выше критической, равной критической и ниже критической. Тройная точка и критическое состояние для воды, нижняя и верхняя пограничные кривые. Области жидкости, влажного и перегретого пара в p - V , T - S и h - S диаграммах.
Уравнение состояния для реального газа pV=zRT z – коэффициент сжимаемости z = 1+B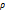 
+C 
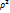+D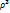 
, где B,C,D – вириальные коэффициенты, учитывающие силы взаимного притяжения и отталкивания.
Уравнение состояния Ван-дер-Ваальса
(p + a/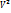 
)(υ - b) = RT
Поправка a/ 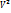учитывает действие сил взаимодействия между молекулами газа, поправка b учитывает размер молекул.
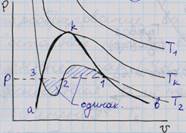
Отрезок 3-1 – реальная изотерма.
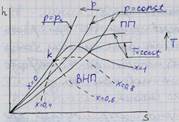
ak – нижняя пограничная кривая (НПК) разделяет жидкую фазу вещества слева и двухфазное состояние (жидкость – пар) справа, в каждой точке НПК начало кипения жидкости.
kb – линия, верхняя пограничная кривая (ВПК), разделяет двухфазное состояние и паровую (газовую) фазу. В каждой точке ВПК – сухой насыщенный пар.
k–критическая точка
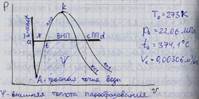
Тройная точка воды:
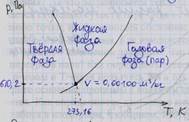
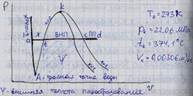
a – жидкость при 0°С
ab – подогрев жидкости при p=constдо температуры кипения (сопровождается испарением – парообразованием поверхности).
b – начало кипения
bc – изобарно-изотермический процесс парообразования с потреблением теплоты при кипении (парообразование во всем объёме).
Состояние пара - влажный насыщенный пар (ВНП) при давлении насыщения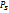 
и температуре насыщения 
.
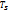с – испарение последней капли жидкости, весь пар сухой, насыщенный.
сd – изобарный перегрев пара, степень перегрева – разность температур перегретого пара и СНП при p=const.
2. Что называется теплотой парообразования? Как она изменяется с ростом давления? На что затрачивается теплота парообразования? Что называется степенью сухости пара? Как ее определить по расположению точки, изображающей состояние в области влажного пара p - V и T - S диаграмм. Теплотой парообразования r, Дж/кг называется количество теплоты, необходимое для полного превращения кипящей 1кг жидкости в сухой насыщенный пар. С ростом давления r уменьшается, в критической точке r = 0.
R = ρ + ψ , где ρ – внутренняя теплота парообразования (изменение внутренней потенциальной энергии), ψ – внешняя теплота парообразования (работа расширения ВНП).
Степенью сухости называется массовая доля сухого пара во влажном паре
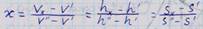
Vx, hx, Sx – объём, энтальпия и энтропия ВНП в данном состоянии.
V’, h’, S’ – объём, энтальпия и энтропия кипящей жидкости (в точке b – начале кипения).
V’’, h’’, S’’ – параметры сухого насыщенного пара (в точке с).
Энтальпия перегретого пара растёт с увеличением давления.
Степень перегрева – разность температур перегретого пара и сухого насыщенного пара при p=const.
3. Рассмотрите основные процессы с водяным паром в p - V и h - S координатах. Как определяются изменение внутренней энергии, теплота и работа в изохорном, изобарном, изотермическом, адиабатном процессах с использованием диаграммы h - S ?
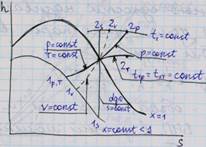
Изобарный процесс 1p2p является процессом расширения и протекает с подводом теплоты.
Степень перегрева Т2р – T1
q = h2-h1 = Δh ,т.к. h = u + pυ
Δu = (h2-p2 υ2) – (h1-p1υ1)
q = Δu + l l = Δh – Δu = p(υ 2- υ 1), l0 = 0
Изотермический процесс 1т2т является процессом расширения и протекает с подводом теплоты.
q = T(S2 - S1) = TΔS
Δu = (h2 - p2υ2) – (h1 - p1υ1) , Δu≠0 как в случае с идеальным газом.
L = q – Δu, l0 = q - Δh (l0 ≠ l в отличие от процесса с идеальным газом).
Изохорный процесс идёт с подводом теплоты и повышением давления и температуры пара. Работа расширения не совершается. На рисунке: 1v2v
q = Δu, Δu = (h2 - p2υ2) – (h1 - p1υ1) = h2 - h1 – υ (p2 - p1) l = 0, l0 = q – Δh = υ (p2 - p1)
Адиабатный процесс 1s2s представляет собой сжатие. Температура растёт, V2S<V1S, p2S>p1S. Затраченная на сжатие работа идёт на изменение внутренней энергии пара Δu = (h2-p2υ2) – (h1- p1V1),
l = -Δu; l0 = -Δh, dq = 0
11. Течение и истечение газов.
1. Сформулируйте и приведите записи закона термодинамики для движущегося газа. Поясните входящие в уравнение величины, запишите условия установившегося трехмерного и одномерного течений газа.
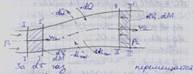
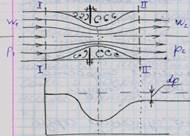
За dτ газ перемещается из I-II в I’-II’
Работа силы давления p1: p1A1w1d*τ = p1dυ 1 = p1 υ 1dM
Работа силы давления p2: -p2A2w2d*τ = -p2d υ 2 = -p2 υ 2dM
Работа проталкивания: dL = (p1υ1 - p2υ2)dM
Энергия, подведенная к газу в выделенном объеме (dQ и dLпрот) затрачивается на изменение внутренней и кинетической энергий газа, а также на совершение газом технической работы.
dQ+dM(p1υ1 – p2υ2) = (u2-u1)dM+0.5(w22 – w12)dM+dLтехн, а для 1кг d q=dh+wdw+dlтехн
Проинтегрировав, q=h2-h1+ (w22-w12)/2 + lтехн
Это уравнение первого закона термодинамики для газовых потоков в «тепловой» форме: теплота, подведенная к потоку газа, равна алгебраической сумме изменения энтальпии газа, совершаемой им технической работы и изменения кинетической энергии потока. dq=dh - vdp, - vdp = wdw + dlтехн или –(dp/ρ)= wdw+dlтехн
Располагаемая работа dl0= -υdp затрачивается на изменение кинетической энергии газа и совершение им технической работы.
Допущение о стационарности течение означает, что параметры потока в каждом сечении не зависят от времени τ
2. Как можно определить теоретическую скорость истечения идеального и реального газов, если предположить, что в пределах канала происходит полное расширение от параметров среды, из которой идет истечение, до параметров среды, в которую идет истечение?
При w2=w и h2=h: w =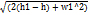 
; это уравнение справедливо как для идеальных, так и для реальных газов (w решается с помощью hs-диаграммы)
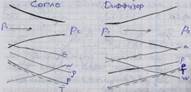
3. Дайте определение сопла и диффузора. Как изменяются вдоль сопла и диффузора удельный объем, скорость, давление, температура, скорость звука при адиабатном течении?
Cопло- канал, в котором с уменьшением давления скорость газа растет (dp<0, dw>0).
Диффузор - канал, в котором скорость газа уменьшается, а давление повышается.
Скорость звука a=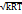 
= 
,
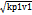(из выражения a =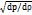 
)
4. Истечение через суживающиеся сопло. 3 характерных случая истечения из суживающегося сопла. В каком из случаев появляется необходимость применения комбинированного сопла (сопла Лаваля)?
Рассмотрим адиабатное истечение газа из ресивера в атмосферу с давлением p0 через суживающееся сопло. Параметры газа в ресивере p1, T1 при истечении не меняются. Скорость w1=0
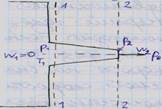
β =p0/p1, βкр=(2/(k+1))k/(k-1). β > βкр – докритический, β = βкр – критический, β < βкр – сверхкритический режимы.
А) β > βкр: давление
понижается от p1 до p2=p0, w2<a2, располагаемая работа
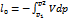полностью расходуется на увеличение кинетической энергии газа.
Б) β = βкр: также происходит полное расширение газа, на срезе сопла p2 = pкр= βкрp1=p0,
скорость на выходе равна критической скорости звука, 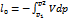полностью расходуется на увеличение кинетической энергии газа.
В) β < βкр: в пределах сопла происходит неполное расширение газа, давление понижается только до критического, на срезе сопла p2=pкр= p1βкр > p0,
скорость на выходе равна критической скорости звука.
Дальнейшее расширение газа и понижение его давления до p0 осуществляется за пределами сопла. На увеличение кинетической энергии расходуется только часть располагаемой работы, другая её часть в суживающимся сопле остается нереализованной.
В третьем случае, β < βкр, для максимального использования располагаемой энергии необходимо применить сопло Лаваля.
5. Как определяются критические значения давления, температуры, удельного объема, скорости газа? Что называется числом Маха?
Критическими называются параметры газового потока, когда скорость газа равная местной скорости звука.
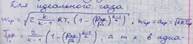
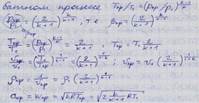
Числом Маха называется отношение скорости газа к местной (в данном сечении канала) скорости звука. M=w/a
Максимальная скорость на выходе из сопла Лаваля может быть достигнута при истечени газа в абсолютный вакуум p0/p1=0
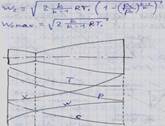
6. Рассмотрите течение с трением, коэффициент скорости, коэффициент расхода. Как определяются коэффициент потерь энергии и КПД сопла?
Действительный процесс истечения реального газа происходит при трении частиц газа между собой и о стенки канала. При этом работа, затрачиваемая на преодоление сил трения, преобразуется в теплоту, в результате чего температура и энтальпия газа в выходном сечении канала возрастают. Истечение газа с трением становится необратимым процессом и сопровождается увеличением энтропии.
Отношение действительного теплоперепада к теоретическому называется КПД канала:
При вычислении расхода газа, помимо уменьшения скорости, учитывается сужение струи:
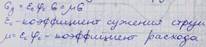
7. Рассмотрите процесс дросселирования, эффект Джоуля-Томсона, дифференциальный и интегральный дроссель- эффекты. Что понимается под температурой инверс?
Дросселирование – необратимый процесс протекания газа (пара) через местное сопротивление, в результате которого понижается давление газа без совершения им технической работы. Процесс дросселирования протекает с увеличением энтропии, после дросселирования удельный объем и скорость газа возрастают (V2>V1, w2>w1), а температура газа, в зависимости от его природы и параметров состояния, может как увеличиваться, так и уменьшаться, либо оставаться неизменной.
При дросселировании принимают h2=h1, u2+p2v2=u1+p1v1
Изменение температуры после дросселирования называется дроссель-эффектом Джоуля-Томсона.
Для идеального газа при h1=h2 и T1=T2 (эффект Джоуля-Томсона равен нулю)
Для реального газа:
- Если lпрот< Δ uпот, то Δ uкин<0, dT<0
- Если lпрот= Δ uпот, то Δ uкин=0, dT=0
- Если lпрот> Δ uпот, то Δ uкин>0, dT>0
Первая производная температуры по давлению при неизменной энтальпии называется дифференциальном дроссель-эффектом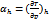 
Дифференциальный дроссель-эффект используется для определения температуры газа после дросселирования при малом уменьшении давления. При значительном уменьшении давления изменение температуры определяется интегральным дроссель-эффектом Джоуля-Томпсона: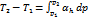 
Температурной инверсии Tинв называется температура, при которой дроссель-эффект равен нулю
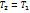
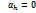
12. Цикл газовой турбины при p = const .
1(2). Приведите схемы газотурбинной установки, работающей по циклу с подводом теплоты при p = const без регенерации и с регенерацией.
Газовая турбина служит для преобразования теплоты в работу. В цикле ГТУ с непрерывным потоком теплота к рабочему телу подводится при постоянном давлении p=const.
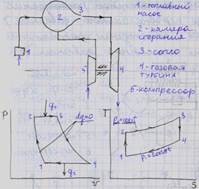
12 - адиабатное сжатие до давления p2 ;
πк = p2/p1 - степень повышения давления, ε=υ1/υ2 - степень сжатия.
23 - подвод теплоты q1 при постоянном давлении p2 (сгорание топлива), β = υ3/υ2 - степень предварительного расширения.