7. Изохорный и изотермический процессы с идеальными газами.

Дата: 2025-05-25; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Параметры и уравнения состояния.

1. Приведите характеристику движения молекул газа. Какие свойства газа опред таким характером движения?

В газах расстояние между молекулами больше размеров молекул, а силы притяжения очень малы. Поэтому газы не имеют собственной формы и постоянного объёма. Газы очень легко сжимаются, так как силы отталкивания также малы, и обладают свойством неограниченно расширяться, заполняя весь предоставленный объём.

2. Поясните физический смысл давления и температуры газа. Приведите единицы их измерения в СИ.

Давление газа - сила газа, действующая на единицу площади стенки сосуда, в котором заключён газ; эта сила обусловлена ударами беспорядочно движущихся молекул газа о стенки сосуда.
[Па, Н/м²], n - концентрация молекул, m - масса молекулы, w²- среднеквадратическая скорость.

Температура - параметр, характеризующий тепловое состояние тела, мера интенсивности теплового движения микрочастиц, среднюю кинетическую энергию теплового движения молекул.

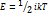, i - число степеней свободы молекул газа (i = 3 для одноатомных газов,

i = 5 для двухатомных, i = 6 для многоатомных), k = 1,38*10^-23Дж/К - постоянная Больцмана.
T – абсол. температура, [К], T = t^oC + 273,15

3. С помощью каких приборов определяется абсолют давление газа?

Абсолютное давление в атмосфере p_абс = p_бар измеряется барометром, мм рт. ст.

В закрытом сосуде при давлении больше атмосферного p_абс = p_бар + p_изб, избыточное давление измеряется манометром, p_изб = p_ман

В закрытом сосуде при давлении меньше атмосферного p_абс = p_бар - p_разр, разрежение измеряется вакуумметром: p_разр = p_вак

4. Приведите обозначения и единицы измерения объема, удельного объема и плотности вещества.

Объём V, м³

Удельный объём - объём единицы массы вещества υ = , м³/кг

Плотность – масса, заключенная в единице объёма вещества ρ = 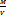= , кг/м³

5. Поясните понятие идеального газа.

Идеальный газ - газ, молекулы которого рассматриваются как материальные точки, взаимодействие между которыми ограничивается абсолютно упругими соударениями, а сами молекулы не имеют объёма, и между ними отсутствуют силы притяжения или отталкивания.

6. Приведите запись уравнений состояния для 1 кг, M кг, 1 кмоля, N кмолей, идеального газа. Поясните физический смысл индивидуальной и универсальной газовых постоянных.

Для 1 кг: pυ = RT Для M кг: pV=MRT

Для 1 кмоля: pυ_µ = R_µT

Для N кмолей: pV = R_µNT

R - индивидуальная газовая постоянная. Представляет собой работу изменения объёма, совершаемую 1 кг рабочего тела при изменении его температуры на 1 К в изобарном процессе, Дж/кг*К.

R_µ - универсальная газовая постоянная, представляющая собой работу изменения объёма, совершаемую 1 килломолем рабочего тела при изменении его температуры на 1 К в изобарном процессе, Дж/кмоль*К.

R_µ = pυ_µ/T, при н.у. p₀ = 101325 Па, T₀ = 273 К, υ_µ = 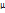*V₀ = 22,4 м³/кмоль(закон Авогадро)

R_µ = 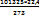= 8314 Дж/кмоль*К или R_µ = k*N_A = 1,38*10^-23*6,022*10²⁶ = 8314 Дж/кмоль*К, г k - постоянная Больцмана,

N_A - число Авогадро

7. Какие условия называются нормальными физическими?

Нормальными называют стандартные физические условия, с которыми обычно соотносят свойства веществ. Они определены следующим образом:

Атмосферное давление: p₀ = 101325 Па = 760 мм рт. ст.

Температура воздуха T₀ = 273,15 К = 0^oC

8. Как определить плотность и удельный объем газа при нормальных физических и произвольных условиях?

При нормальных: υ₀ = υ_µ/ 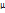= 22,4/µ , м³/кг

ρ = 1/υ₀ = 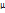/υ_µ = µ/22,4 , кг/м³ , µ - молярная масса газа

При произвольных: υ = RT/p, где R = R_µ/µ = 8314/µ , Дж/кг*К ρ = 1/υ = p/RT

2. Смеси идеальных газов.

1. Поясните понятия: массовая доля, объемная (мольная) доля компонентов. Как определить массовые доли, если смесь задана объемными долями и как определить объемные доли, если смесь задана массовыми долями.

Массовая доля компонента смеси есть отношение массы компонента к массе смеси g_i = M_i/M, ∑g_i = 1

Объёмная доля компонента смеси - отношение объёма компонента к объёму вей смеси: r_i = V_i/V, ∑r_i = 1

Молярная для - отношение числа киломолей компонента к числу компонентов смеси: n_i = N_i/N,

Связь между массовыми и объёмными долями смеси:

g_{i = Mi/M=Ni 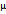i}/Nµ=r_i* 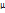_i/µ= r_i*R/Ri r_i = g_i*µ/ 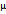_i=giRi/R

µ - молекулярная масса смеси

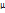µ = ∑ _i*r_i или µ = 1/∑(g_i/ _i)

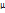_i - молекулярная масса компонента

2. Поясните понятия: парциальное давление и парциальный объем. Сформулируйте закон Дальтона.

Парциальное давление - давление, которое имел бы газ, входящий в состав смеси, если бы он один занимал объём, равный объёмы смеси, при той же температуре.

Парциальный объём - объём, который занимал бы компонент смеси при температуре и давлении смеси.

Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений каждого газа смеси.

p = ∑p_i ; p_i = p*r_i

3. Поясните смысл понятия "кажущаяся молекулярная масса смеси". Как определяется кажущаяся молекулярная масса, газовая постоянная, плотность и теплоемкость газовой смеси?

Кажущаяся молекулярная масса смеси газов - отношение общей массы смеси к общему числу молей всех компонентов смеси.

µ = M/N = ∑M_i/∑N_i ; µ = ∑ µ_i*r_i = 1/∑(g_i/µ_i)

Газовая постоянная смеси: R = ∑R_i*g_i

Плотность смеси газов: ρ_см = M_см/V_см = M_см/∑V_i = M_см/∑(M_i/ρ_i) = 1/∑(g_i/ρ_i)

Теплоёмкость газовых смесей:

Массовая с = ∑c_i*g_i ; c = c/m

Объёмная c' = ∑c'_i*r_i ; c' = c/V

Молярная c_µ = µ*c = ∑ c_µi*r_i ; c_µ = c/N

3. Теплоемкость газов и паров.

1. Приведите определение понятия "удельная теплоемкость". Рассмотрите зависимость теплоемкости: от характера процесса, природы вещества и состояния газа ( T , p )

Удельная теплоёмкость - количество теплоты, необходимое для изменения температуры единицы количества газа в данном процессе на 1 К.

В зависимости от единицы количества газа используется теплоёмкость: массовая (c, Дж/кг*К), объёмная (c' , Дж/м³*К), молярная (c_µ , Дж/кмоль*К)

Влияние характера процесса подвода (отвода) теплоты: в общем случае теплота затрачивается на изменение внутренней энергии газа и на совершение им работы. Чем больше доля подводи мой теплоты, которая идёт на совершение работы, тем больше теплоёмкость.

Влияние природы газа: чем больше атомов в молекуле (не более трёх), тем больше теплоёмкость.

Влияние температуры: теплоёмкость двух- и многоатомных газов с ростом температуры увеличивается, а показатель адиабаты уменьшается (k = c_p/c_v). Теплоёмкость и показатель адиабаты одноатомного газа от температуры не зависят.

Теплоёмкость реальных газов зависит

также от давления, но зависимость незначительна.

2. Почему теплоемкость в изобарном процессе больше, чем в изохорном? Запишите уравнение Майера.

В изохорном процессе вся подводимая теплота идёт на изменение внутренней энергии, а в изобарном часть теплоты затрачивается на совершение газом работы, для 1 кг газа при ΔT = 1 К: C_v = ΔU ; C_p = ΔU + L ; C_p - C_v = L, где L - работа 1 кг газа при нагревании на 1 К при постоянном давлении, по этому определению L = R.

Уравнение Майера: C_p - C_v = R

C_pµ - C_vµ = R_µ = 8314 Дж/кг*К

3. Как определить среднюю для интервала температур T 1- T 2 теплоемкость, пользуясь табличными значениями средних теплоемкостей от О до T ? Как определить среднюю для интервала температур теплоемкость, пользуясь зависимостью истинной теплоемкости от температуры?

Истинная теплоёмкость - отношение бесконечно малого количества теплоты, подведённого к единице газа, к вызываемому при этом бесконечно малому повышению его температуры.

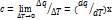
Средняя теплоёмкость – рабочего тела в данном процессе в интервале температур Т1…Т2 – отношение удельного количества теплоты q, сообщаемого рабочему телу, к разности конечной и начальной температур

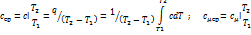
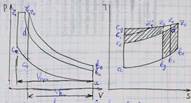
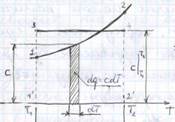Геометрически средняя теплоёмкость – высота прямоугольника 13421, площадь котрого равна 1221 под кривой от точек 1и2

По сред теплоёмкостям определяют теплоту в любом интервале температур.

При известной зависимости 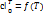в процессе 1-2 ,

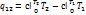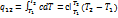
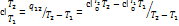
По зависимости истинной теплоемкости c=f(T), вместо интегрирования приближенно определяют 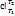при средней температуре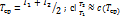

4. Как определить удельную массовую теплоемкость смеси газов, зная теплоемкости компонентов? Как определить объемную и мольную теплоемкость, зная массовую?

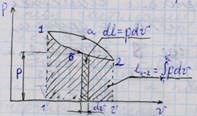При расчётном определении теплоёмкости смеси газов исходят из того, что для нагревания смеси надо нагреть в том же интервале температур каждый из её компонентов: .

Разделив это на MΔT, получим

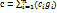. Если смесь задана массовыми долями g_i, то надо найти массовую теплоёмкость по значениям массовых теплоёмкостей c_i её компонентов. Определяют объёмную и молярную теплоёмкости смеси: .

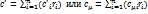Массовая теплоёмкость c = C/m:

Объёмная теплоёмкость c' = C/V = c*ρ,

V и ρ - объём и плотность тела при нормальных физических условиях.

Мольная теплоёмкость: c_µ = C/N,

N - количество газа в кмолях

c = c_µ/µ или c_µ = µ*c

4. Первый закон термодинамики.

1. Поясните физический смысл функций состояния: Приведите качественную характеристику зависимости внутренней энергии и энтальпии от состояния газа.

Внутренняя энергия - все виды энергии, связанные с внутренним тепловым движением молекул и их взаимодействиями. В общем случае, внутренняя энергия газа состоит из кинетической энергии движения молекул, которая зависит только от температуры газа, а также потенциальной энергии взаимодействия молекул между собой, зависящей от среднего расстояния между молекулами, т. е. от занимаемого газом объёма, энергии, обусловленной действием внутриатомных и внутриядерных сил. Внутренняя энергия зависит от температуры и объёма и является функцией этих параметров состояния U = f (T, υ). Изменение внутренней энергии зависит от начального и конечного состояния газа: ΔU = U₂ - U₁

Если процесс замкнут, то ΔU = 0.

Для идеального газа потенциальная энергия равна нулю (отсутствуют силы между частицами) U = U_кин , dU = C_vdT ;

ΔU = C_v (T₂ - T₁)

Энтальпия - сумма внутренней энергии и потенциальной энергии давления

H = U + pV h = u + pv

Энтальпия зависит от параметров состояния p, υ, T. Энтальпия идеального газа является функцией температуры

h = U(T) + RT

2. Как вычисляются изменения внутренней энергии и энтальпии для идеального газа? Как вычисляются количество теплоты, работа и техническая работа (располагаемая эн)?

Для идеального газа:

dU = C_vdT , ΔU = C_v(T₂ - T₁)

h=u+pv=u+RT dh = du+RdT= (C_v+R)dT= C_pdT Δh = C_p(T₂ - T₁)

Количество теплоты - количественная мера энергии, передаваемой одним телом другому при их взаимодействии, зависящей от температуры этих тел и не связанная с переносом вещества от одного тела к другому.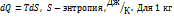

.

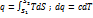Работа - количественная мера макроскопической формы энергообмена между телами, осуществляемая перемещением тела или изменением его объёма.

Элементарная работа, совершаемая при перемещении поршня dL = PdS = pAdS = pdV, p - давление газа, А - площадь поршня, dS - элементарное перемещение, dV - элементарное изменение объёма.

Для 1 кг dl = pdv ; .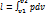

В p-V координатах площадь под линией процесса соответствует работе.

L_1a2 - площадь 1'1a22'1' , L_1б2 - площадь 1'1б22'1' , L_1a2 > L_1б2 , значит работа зависит от пути процесса.
Располагаемая работа - работа изменения давления или работа, которую может совершить рабочее тело при истечении в окружающую среду под действием разности давлений рабоч тел, сред

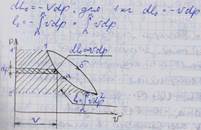
В p-V координатах площадь правее линии процесса соответствует располагаемой работе

L_{0 1а2} - площадь 1'1а22'1' , L_{0 1б2} - площадь 1'1б22'1' , L_{0 1а2} < L_{0 1б2} - располагаемая работа зависит от пути процесса.

3. Сформулируйте первый закон термодинамики и приведите его аналитические выражения. Что понимается под вечным двигателем первого рода?

Первый закон термодинамики - частный случай всеобщего сохранения энергии: энергия не исчезает и не создаётся вновь, она лишь может переходить от одного тела к другому или превращаться из одного вида в другой в равных количествах.

Теплота, подводимая к рабочему телу, затрачивается на изменение его внутренней энергии и совершение им работы. ΔU=U2-U1=Q-L

Для элементарного терм процесса:

dQ=dU+dL для 1 кг: dq=du+dl

q=Δu+l=Cv(T2-T1)+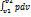

Невозможно в каком-либо механизме периодически получать работу, не подводя энергию извне. Вечный двигатель первого рода невозможен. Вечный двигатель первого рода - гипотетический двигатель, способный производить работу, не получая энергию извне.

Теплота, подведённая к рабочему телу, расходуется на увеличение его энтальпии и располагаемой работы.

dq=dh+dlо; q=Cp(T2-T1)-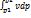

4. Поясните, что понимается под равновесным состоянием. Какие процессы называются обратимыми? Какие условия осуществления обратимых процессов?

Состояние термодинамической системы равновесное, если каждый из параметров состояния имеет одинаковые численные значения во всех точках системы. Процесс, при котором система проходит через равновесные состояния - равновесный.

Обратимый процесс - процесс, который может происходить как в прямом, так и в обратном направлении, причём при возвращении в первоначальное состояние система проходит все равновесные состояния прямого процесса, но в обратном порядке.

Условия обратимости процесса:

- бесконечно медленное его прохождение при бесконечно малой разности давлений термодинамической системы и окружающей среды.

- теплообмен между термодинамической системой и окружающей средой при бесконечно малой разности температур.

5. Рассмотрите работу расширения и работу против внешних сил при обратимом и необратимом процессах.

В диаграммах состояния P, V и других круговые процессы изображается в виде замкнутых кривых. В любой диаграмме два тождественных состояния (начало и конец кругового процесса) изображаются одной и той же точкой на плоскости.

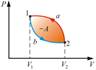
Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1 – 2) и сжатия (2 – 1) газа. Работа расширения (определяется площадью фигуры 1a2V₂V₁1) положительна (dv>0). Работа, совершаемая за цикл, определяется площадью, охваченной замкнутой кривой.

Если к рабочему телу подвести какое-то количество теплоты dq от источника с температурой Т₁, то тело при расширении совершит работу dl против внешних сил. В равновесном процессе температура рабочего тела Т будет равна температуре источника, т. е. Т=Т₁, и при расширении тела нет ни внутреннего ни внешнего трения. Работа расширения равна dl_{равнов.} = Pdυ и изменение энтропии ds_равнов = dq/T.

В неравновесном процессе, имеет место внутреннее или внешнее трение, то совершаемая работа против сил трения, будет меньше на величину затраченной работы на преодоление трения и переходит в теплоту трения dq_тр.

Рабочее тело воспринимает эту теплоту вместе с подведенной теплотой, в результате энтропия возрастает в неравновесном процессе по сравнению с равновесным, хотя к рабочему телу было подведено от источника теплоты одинаковое количество кол-во теплоты dq.

6. T - S диаграмма. Определение теплоты, изменения внутренней энергии, изменения энтальпии, работы, технической работы (располагаемой энергии) с использованием T - S диаграммы.

Особенностью Т-S координат является то, что площадь под линией процесса соответствует количеству энергии отданной или полученной рабочим телом.

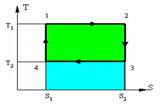
Т - S диаграмма цикла Карно

На данной диаграмме представлен некий замкнутый цикл. Система последовательно

переходит из точки 1 в 2 затем 3, 4 и снова в 1. Из графика видно что процесс 1 2-изотермический (происходит при Т₁) и процесс 3 4 также изотермический (происходит при T₂)

Процессы 23 и 41 -адиабатные. Поскольку в них не происходит изменение энтропии то dS =0 следовательно dQ = 0 или Q = const.

Количество тепла подводимое к системе:

Q₁ = T₁ *(S₂-S₁) площадь прямоугольника

1-2-S₂-S₁-1

Количество тепла отдаваемое системой:

Q₂ = T₂ (S₂-S₁) площадь прямоугольника

3-S₂-S₁-4-3

Работа цикла L = Q₁- Q₂

К.П.Д цикла ᵑ=(Q1-Q2)/Q1

5. Термодинамические процессы с идеальными газами.

1. Какие процессы называются политропными? Как определить теплоемкость и коэффициент разветвления теплоты в произвольном политропном процессе?

Политропный процесс – процесс, протекающий при неизменной теплоёмкости. p =const

n= 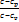- показатель политропы

c= 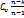- теплоёмкость политропного проц

k= 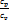- показатель адиабаты

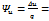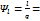При условии независимости теплоёмкости от температуры в политропном процессе остаётся неизменным и распределение подведённой теплоты на изменение внутренней энергии рабочего тела и совершение работы: const const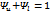

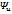-коэффиц разветвления теплоты

q= 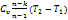, ΔU= ,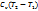

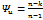
2. Рассмотрите изохорный, изобарный, изотермический и адиабатный процессы как частные случаи политропных процессов.

Изохорный процесс - процесс, протекающий при постоянном удельном объёме.

Уравнение процесса υ = const получается из уравнения политропного процесса

pυⁿ = const или p^1/n υ = const при n = ±∞ . Теплоёмкость процесса C = C_v .

Изобарный процесс протекает при постоянном давлении. Уравнение процесса p = const получается из уравнения политропного процесса pυⁿ = const при n = 0. Теплоёмкость процесса C = C_{p .}

Изотермический процесс - процесс, при котором температура остаётся неизменной на протяжении всего процесса. Уравнение процесса T = const получается из уравнения политропного процесса pυⁿ = const при n = 1. Теплоёмкость процесса C = ∞ .

В адиабатическом процессе отсутствует теплообмен между телом и окружающей средой, dq = 0 ; du + dl = dq ; C_vdT + pdV = 0

Уравнение процесса pυ^k = const, то есть n = k, теплоёмкость C = 0.

3. Как вычисляются теплота, работа, техническая работа (располагаемая энергия), изменения внутренней энергии, энтальпии и энтропии в произвольных политропных процессах?

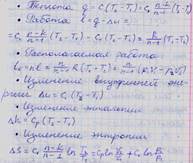
4. Рассмотрите способ построения графиков политропных процессов в p - V координатах. Приведите сводные графики политропных процессов в p - V и T - S координатах. Как определить показатель политропы, имея график процесса в p - V координатах?

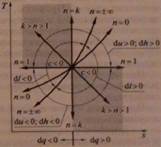
При dV > 0 происходит расширение газа с совершением работы (dl > 0), при dυ < 0 - сжатие газа с затратой работы (dl < 0).

- Чем больше показатель политропы n, тем круче линия процесса.

- В процессах, линии которых находятся правее адиабаты, теплота q подводится, левее - q отводится.

- В процессах, линии которых расположены выше изотермы, T увеличивается, ниже - T уменьшается.

- В процессах, линии которых расположены между адиабатой и изотермой теплоёмкость отрицательна (при расширении с подводом q температура уменьшается, при сжатии с отводом теплоты температура увеличивается).

Определение показателя политропы в p-V координатах:

pυⁿ = const, прологарифмируем это уравнение, lnp = const - n*lnυ.

В логарифмических координатах политропа представляет собой прямую с угловым коэффициентом равным n. n=tgφ=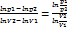

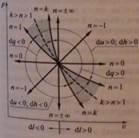
5. Рассмотрите 3 характерные группы политропных процессов. Для каждой из них приведите знаки dp , dT , dh . Приведите пределы изменения показателя политропы и коэффициента разветвления теплоты для каждой группы.

Первая группа процессов располагается между изобарой и изотермой (0 < n < 1). Диапазоны изменения коэффициентов разветвления теплоты и теплоёмкости:

> Ψ_u > 0, c_p < c < +∞

При расширении газа: dq>0, du>0, dl>0,

dp < 0, dT > 0, dh > 0

При сжатии газа: dq<0, du<0, dl<0.

dp > 0, dT < 0, dh < 0

Вторая группа процессов располагается между изотермой и адиабатой (1 < n < k). Диапазоны изменения коэффициентов разветвления теплоты и теплоёмкости:

0 > Ψ_u > -∞, 1 > Ψ_l < +∞, -∞ < c < 0

При расширении газа: dp < 0, dT < 0, dh ≤ 0

При сжатии газа: dp > 0, dT > 0, dh ≥ 0

Особенность процессов второй группы - отрицательное значение теплоёмкости, что означает уменьшение температуры при подводе теплоты или её увеличение при отводе теплоты.
Третья группа процессов располагается между адиабатой и изохорой (k < n < +∞). Диапазоны изменения коэффициентов разветвления теплоты и теплоёмкости:

+∞ > Ψ_u > 1, 0 < Ψ_l <1, 0 < c < c_υ

При расширении газа: dp < 0, dT < 0, dh < 0

При сжатии газа: dp > 0, dT > 0, dh > 0

6. Адиабатный процесс с идеальными газами.

1. Рассмотрите зависимость показателя адиабаты от природы и состояния газа. Приведите графики адиабатного процесса в p - V и T - S координатах.

Показатель адиабаты:k = 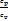= 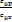;c_p - c_v= R c_µp - c_µv = R_µ 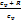;k = = 1 + или k = 1 +

Показатель адиабаты k возрастает с уменьшением теплоёмкости.

Теплоёмкость зависит от числа степеней свободы молекулы, зависящей от числа атомов в молекуле. Теплоёмкость идеального газа возрастает с увеличением числа атомов в молекуле. Уменьшается значение показателя адиабаты k. Это справедливо для молекул с числом атомов не более трёх.

С уменьшением температуры происходит "вымораживание" числа степеней свободы, что снижает энергию движения молекул и приводит к снижению теплоёмкости. С увеличением температуры возбуждаются дополнительные степени свободы за счёт колебательных движений атомов внутри молекул, что увеличивает теплоёмкость.

2.Поясните, как вычисляются изменения внутренней энергии, энтальпии, работа, техническая в адиабатном процессе. Дайте качественную в виде схемы характеристику энергетических превращений в процессе.

l=-ΔU ΔU = c_v(T₂ - T₁) - изменение внутренней энергии;

Δh = c_p(T₂ - T₁) - изменение энтальпии;

l = -ΔU = c_v(T₁ - T₂) = (T₁ - T₂) = (p₁v₁ - p₂v₂) - работа (k - показатель адиабаты);

l₀ =kl; l₀ = 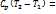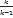R(T₁ - T₂) =

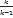(p₁v₁ - p₂v₂) - техническая работа. =∞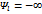

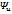3. Рассмотрите необратимый адиабатный процесс и приведите его условное изображение в T - S координатах.

Обратимый адиабатный процесс может быть реализован в системе, границы которой абсолютно непроницаемы для теплообмена, а сам процесс протекает бесконечно медленно. dq = Tds, в обратимом процессе ds = 0, т.е. энтропия не изменяется. Такой процесс- изоэнтропийным.

Не всякий адиабатный изоэнтропийный. При течении реального газа по шероховатой трубе с идеальной изоляцией теплообмен со стенками практически исключается, что позволяет считать этот процесс адиабатным. Из-за трения энергия рассеивается и процесс становится необратимым, что приводит к росту энтропии.

В реальных условиях адиабатными процессами являются процессы, в которых теплообмен пренебрежимо мал по сравнению с энергообменом в форме работы. Такое возможно в процессах, протекающих в течение коротких промежутков времени и в которых теплообмен со стенками незначителен.

Необратимый адиабатный процесс:

dq < Tds, т.к. dq = 0, Tds > 0.

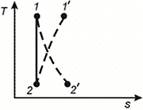
Возрастание энтропии происходит как при расширении газа (процесс 1 – 2’) так и при сжатии (процесс 2 – 1’). Площадь под кривой процесса в Т-s координатах изображает теплоту трения.

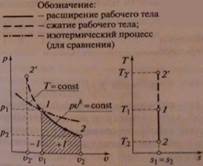
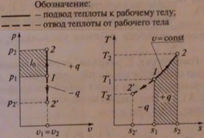
7. Изохорный и изотермический процессы с идеальными газами.

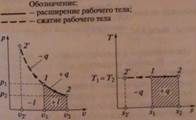1. Приведите уравнения и графики процессов в p - V и T - S координатах, формулы соотношения между параметрами. Дайте характеристику теплоёмкостей в процессах.

Изохорный:

Уравнение процесса V=const получается из уравнения политропного процесса

pvⁿ = const при n → ±∞

Соотношение параметров: 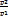= 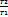( = const

При n → ±∞ удельная теплоёмкость:

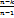c = c_υ = c_υ

Изотермический:

Уравнение процесса выводится из уравнения состояния идеального газа

pv = RT. При T = const: pv = const

Или из уравнения политропного процесса pvⁿ = const при n = 1.

Соотношение параметров: =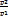

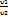
(pv = const)

В элементарном процессе количество энергии, подводимой или отводимой в форме теплоты, выражается как: dq = cdT, при dT=0: c = = ±∞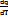

2. Как вычисляются теплота, изменение внутренней энергии, энтальпии, энтропии, работа и техническая работа (располагаемая энергия)?

Изохорный процесс:

,

,

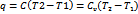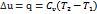Δh= ,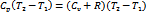

Δs= 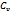ln

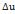l=q - =0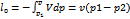

Изотермический процесс:

q= 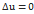; Δh=0;

Δs=Rln =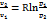

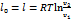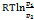
3. Что называется коэффициентом разветвления теплоты? Какие он принимает значения в рассматриваемых процессах? Приведите качественную в виде схемы характеристику энергетических превращений в процессах.

Коэффициент разветвления теплоты 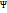_U - доля теплоты, затрачиваемая на изменение внутренней энергии. Он равен отношению теплоты, затраченной на изменение внутренней энергии, к самой теплоте: 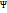_U = 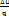= const

8. Второй закон термодинамики.

1. Какие круговые процессы (циклы) называются прямыми и какие обратными? Что называется термическим КПД и средним давлением цикла? Что они характеризуют? Рассмотрите прямой обратимый цикл Карно. Изобразите его в p - V и T - S координатахЦиклом называется совокупность термодинамических процессов, в результате осуществления которых рабочее тело возвращается в исходное состояние.

Прямой цикл - цикл, в котором теплота превращается в работу (линия расширения проходит выше линии сжатия, цикл протекает по направлению часовой стрелки)

Обратный цикл - цикл, в котором теплота от "холодного" источника передаётся "горячему" источнику при затрате работы (линия сжатия проходит выше линии расширения).

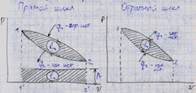
Термический КПД цикла (прямого) есть отношение полезной работы цикла к затраченной теплоте. Термический КПД является экономическим показателем цикла.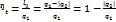

Среднее давление цикла - условное постоянное давление, при котором совершается работа, равная работе за цикл при переменном давлении; по физическому смыслу P_t - работа, приходящаяся на единицу рабочего объёма .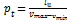

Среднее давление цикла является энергетическим показателем цикла.

Прямой обратимый цикл Карно является самым экономичным циклом. Цикл состоит из двух изотермических и двух адиабатных обратимых процессов при наличии двух источников теплоты - "горячего" и "холодного".

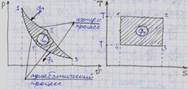
12 - изотермическое расширение (T₁ = const), 23 - адиабатическое расширение (dq = 0), 34 - изотермическое сжатие (T₂ = const), 41 - адиабатное сжатие (dq = 0).

Термический КПД цикла Карно

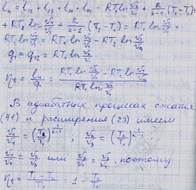
КПД цикла Карно зависит от максимальной (T₂) и минимальной (T₁) температур. КПД растёт с увеличением максимальной и уменьшением минимальной температуры. КПД нельзя получить равным 1.

Термический КПД цикла Карно не зависит от природы рабочего тела (теорема Карно).

Обратный обратимый цикл Карно состоит из следующих процессов: 12 - адиабатное расширение, 23 - изотермическое расширение, 34 - адиабатное сжатие, 41 - изотермическое сжатие.

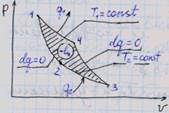
В процессе 23 (T₂ = const) к рабочему телу подводится теплота q₂ от "холодного" источника, в процессе 41 (T₁ = const) теплота q₁ отводится в "горячий" источник.

Обратные циклы характерны для холодильных машин и тепловых насосов.

Для осуществления цикла затрачивается работа l_ц .

2. Приведите формулировки второго закона термодинамики. Что понимается под вечным двигателем второго рода? Рассмотрите круговой интеграл приведенной теплоты для произвольного обратимого цикла. Сравните круговой интеграл приведенной теплоты в обратимом и необратимом циклах. Отличается ли изменение энтропии в обратимых и необратимых процессах при одинаковых начальных или конечных параметрах?

По Больцману: природа стремится к переходу от менее вероятных состояний к более вероятным. Наиболее вероятное состояние термодинамической системы - состояние внутреннего равновесия.

Работа превращается в теплоту непосредственно и полностью. Теплота превращается в работу посредством рабочего тела (газ, пар) лишь частично и при определённых условиях.

Томсон: невозможно превратить в работу энергию какого-либо тела, не производя никакого другого действия, кроме охлаждения этого тела.

Оствальд: вечный двигатель второго рода невозможен. Вечный двигатель второго рода - воображаемый тепловой двигатель, в котором возможно полное превращение подведённой теплоты в работу.

Теплота не может самопроизвольно переходить от более холодного к более тёплому телу.

Произвольный цикл заменяется суммой элементарных циклов Карно.

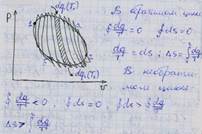
При одинаковом изменении приведённой теплоты в необратимом процессе изменение энтропии возрастает по сравнению с изменением энтропии в обратимом процессе.

В замкнутой системе при передаче теплоты от тела А с более высокой температурой телу Б энтропия тела А уменьшается, а тела Б возрастает

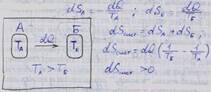
В необратимом процессе энтропия возрастает.

Рассмотрим два цикла Карно. В первом случае теплота dq подводится к рабочему телу непосредственно от тела А, во втором - теплота dq сначала передаётся от тела А телу Б, а затем - от тела Б рабочему телу.

С переходом теплоты на более низкий температурный уровень энтропия растёт, а работоспособность рабочего тела снижается пропорционально росту энтропии.

9. Циклы поршневых двигателей.

1. Почему цикл Карно не применяется в качестве цикла поршневого двигателя?

Для осуществления цикла Карно в интервале реальных рабочих температур современных ДВС степень сжатия должна быть в 40-50 раз больше, чем в поршневых двигателях.

Цикл характеризуется невысоким показателем энергетической эффективности, что выражается в низком значении среднего давления цикла p_{t .}

Отношение среднего давления цикла к максимальному давлению в цикле Карно составляет около 0,2%, тогда как в поршневых ДВС значение этого показателя составляет не менее 10%.

В машинах с однофазным рабочим телом, к которому относится идеальный газ, практически невозможно организовать изотермический подвод и отвод теплоты.

2. Продолженное расширение вполне возможно реализовать в поршневом двигателе. Практически любой ДВС, можно дооборудовать дополнительными блоками цилиндров, для использования режима ПР. На практике, для испольм мования остаточной энергии выхлопных газов, более эфективным является использование турбины.
Наиболее распространеные двигатели с ПР – это дизели с газотурбинным наддувом. Они представляют собой комбинированную теплосиловую установку. Первая ступень – поршневой двигатель, вторая – турбина. Рабочий цикл установки отличается ПР продуктов сгорания почти до атмосферного давления в газовой турбине.
Режим с ПР часто используется в роторно-лопастных и роторно-волновых ДВС.

3. Проанализируйте уравнения термического КПД и среднего давления для цикла со смешанным подводом теплоты. Запишите уравнения для двух других циклов – с подводом теплоты при постоянном объеме и при постоянном давлении.

Цикл Тринклера (Сабатэ) – цикл со смешанным подводом теплоты q – частично при p=const и частично при v=const Vc- объем камеры сгорания

Va- полный объем Vh- рабочий объем

Vh=Va-Vc

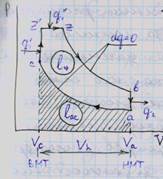
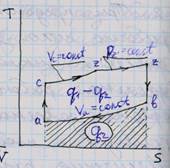
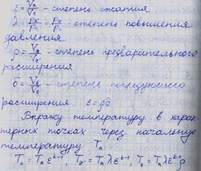
4.Анализ влияния на кпд и среднее давл

КПД цикла растет при уменьшении вычитаемой из 1 дроби: при увеличении степени сжатия ℇ и показателя адиабаты k, зависящего от природы рабочего тела, от степени повышения давления λ, при уменьшении степени предварительного расширения ρ. При продлении изобарного процесса подвода теплоты q1 и увеличения степени предварительного расширения ρ колво отводимой теплоты q2 увелич в большей степени, чем колво подводимой теплоты. Увеличение степ предварительного расширения ρ приводит к уменьшению степени термич КПД.

При увеличении колва подводимой теплоты одновременно возрастают λ и ρ, но ρ оказывает большее влияние на терм КПД, чем λ. Поэтому терм КПД понижается.

Среднее давление цикла растет при увеличении всех величин, стоящих в числителе. Для увелич среднего давления начальное давление pa повышают с помощью наддува. В цикле Тринклера.

5. Сравнение циклов в PV , ST , когда совпадают начальные параметры, природа тела, степень сжатия и работа.

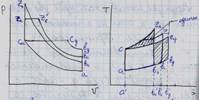
6. Сравнение циклов в PV , ST , когда совпадают начальные параметры, природа тела, макс давление и работа.